Ранговые показатели изменения структуры
Для измерения различий структуры часто используют менее точные, но более простые по расчету показатели, которые основаны на оценки различий не самих значений долей, а их рангов, то есть порядковых номеров. Для этого чаще всего используются 2 показателя[29] – линейный и квадратический коэффициенты изменения (различия) рангов долей. Эти показатели как правило применяются для анализа структуры распределения описательных (атрибутивных) признаков (например, таблица 20), а также для оценки вотумов (голосований).
В 5-м и 6-м столбцах таблицы 21 определены ранги по данным таблицы 20, а в последующих приведены вспомогательные расчеты, необходимые в дальнейшем.
Таблица 21. Вспомогательные расчеты для определения ранговых показателей изменения структуры
| № группы (j) | Имеют образование | d0 | d1 | Ранг мужчин R0 | Ранг женщин R1 |  |  |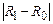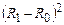
| Высшее профессиональное | 0,087 | 0,130 | |||||
| Неполное высшее профессиональное | 0,019 | 0,023 | |||||
| Сpеднее профессиональное | 0,130 | 0,221 | |||||
| Начальное профессиональное | 0,200 | 0,149 | |||||
| Сpеднее (полное) общее | 0,398 | 0,338 | |||||
| Основное общее | 0,148 | 0,121 | |||||
| Начальное общее, не имеют образ-я | 0,018 | 0,018 | |||||
| Итого | 1,000 | 1,000 |
Линейный коэффициент различия рангов долей (ЛКR) – это отношение фактической суммы модулей изменения рангов к предельно возможной сумме модулей при k элементах структуры. Для четного k определяется по формуле (62), а для нечетного k – по формуле (63):
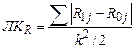, (62) 
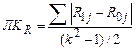, (63)
где R1j и R0j – ранги доли j-го элемента структуры (группы) в сравниваемых совокупностях.
Так по данным таблицы 21, где в предпоследнем столбце рассчитана сумма модулей различий рангов, по формуле (63):
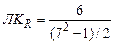= 6/24 = 0,25, то есть различие структуры безработных среди женщин и мужчин по уровню образованию ощутимо и составляет 25% от максимально возможного.
Квадратический коэффициент различия рангов долей (ККR) основан на коэффициенте корреляции рангов Спирмена, особенностью которого является то, что он позволяет определить корреляцию по таким признакам, которые нельзя выразить численно, но можно проранжировать (об этом будет подробно рассказано позднее – в теме 7.4). При полном совпадении рангов долей в базисном и отчетном периодах коэффициент Спирмена равен +1, а при максимальном различии рангов (первый становится последним, порядок рангов «переворачивается») коэффициент Спирмена составит –1, следовательно максимальное значение изменения коэффициента Спирмена равно 2. Чтобы получить показатель степени (существенности) различия рангов элементов структуры, следует отклонение фактического коэффициента Спирмена от единицы разделить на 2:
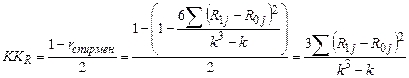. (64)
Для расчета квадратического коэффициента различия рангов долей необходима сумма квадратов различий рангов, которая рассчитана в последнем столбце таблицы 21, тогда по формуле (64):
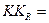
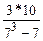= 30/336 = 0,089, то есть различие структуры безработных среди женщин и мужчин по уровню образованию составляет 8,9% от максимально возможного.
Контрольные задания
Вариант 1. По данным ФСГС о распределении численности занятых в экономике России по уровню образования, представленным в таблице 22, проанализировать различия в структурах распределения среди мужчин и женщин.
Таблица 22. Варианты выполнения контрольного задания
| Год (вариант) | Имеют образ-е Доля | Высшее профес-сиональное | Неполное высшее профес-сиональное | Сpеднее профес-сиональное | Начальное профес-сиональное | Сpеднее (полное) общее | Основное общее | Начальное общее, не имеют образ-я |
| 1995 (1) | мужчин женщин | 0,160 0,192 | 0,017 0,014 | 0,276 0,387 | … … | 0,377 0,299 | 0,149 0,096 | 0,021 0,012 |
| 1997 (2) | мужчин женщин | 0,184 0,220 | 0,019 0,018 | 0,280 0,377 | 0,073 0,049 | 0,292 0,238 | 0,124 0,081 | 0,028 0,017 |
| 1998 (3) | мужчин женщин | 0,189 0,226 | 0,019 0,019 | 0,290 0,384 | 0,088 0,060 | 0,279 0,225 | 0,113 0,072 | 0,022 0,014 |
| 1999 (4) | мужчин женщин | 0,184 0,222 | 0,022 0,023 | 0,290 0,377 | 0,107 0,068 | 0,268 0,214 | 0,101 0,071 | 0,028 0,025 |
| 2000 (5) | мужчин женщин | 0,186 0,228 | 0,041 0,048 | 0,247 0,317 | 0,128 0,095 | 0,267 0,219 | 0,107 0,076 | 0,024 0,017 |
| 2001 (6) | мужчин женщин | 0,205 0,250 | 0,024 0,027 | 0,266 0,349 | 0,146 0,090 | 0,258 0,216 | 0,090 0,060 | 0,011 0,008 |
| 2002 (7) | мужчин женщин | 0,198 0,249 | 0,023 0,026 | 0,280 0,353 | 0,139 0,087 | 0,265 0,220 | 0,087 0,057 | 0,008 0,008 |
| 2003 (8) | мужчин женщин | 0,205 0,248 | 0,020 0,022 | 0,211 0,317 | 0,198 0,130 | 0,264 0,210 | 0,093 0,064 | 0,009 0,009 |
| 2004 (9) | мужчин женщин | 0,215 0,262 | 0,019 0,022 | 0,203 0,312 | 0,219 0,133 | 0,255 0,213 | 0,083 0,052 | 0,006 0,006 |
| 2006 (10) | мужчин женщин | 0,235 0,279 | 0,017 0,018 | 0,198 0,315 | 0,218 0,142 | 0,255 0,196 | 0,072 0,045 | 0,005 0,005 |
Выборочное наблюдение