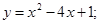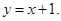Аналитическая геометрия, векторная алгебра
I. Аналитическая геометрия и линейная алгебра
1. Декартова прямоугольная система координат на плоскости и в пространстве. Длина отрезка. Деление отрезка в заданном отношении.
2. Векторы на плоскости и в пространстве. Сложение векторов и умножение вектора на скаляр. Коллинеарность и компланарность векторов.
3. Проекция вектора на ось; теоремы о проекциях. Понятие базиса. Разложение вектора по ортонормированному базису. Операции над векторами, заданными в координатной форме.
4. Скалярное произведение двух векторов, его основные свойства. Угол между двумя векторами. Условия параллельности и перпендикулярности двух векторов.
5. Уравнение линии на плоскости. Уравнения окружности, эллипса, гиперболы, параболы.
6. Различные виды уравнений прямой на плоскости. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Точка пересечения прямых. Расстояние от точки до прямой.
7. Уравнение поверхности. Уравнение сферы.
8. Общее уравнение плоскости. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей. Расстояние от точки до плоскости.
9. Уравнения прямой в пространстве. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
10. Определители и матрицы.
11. Решение систем линейных уравнений.
II. Дифференциальное исчисление
1. Функция и способы ее задания. Область определения и область значения функции.
2. Понятие предела функции; основные теоремы о пределах. Замечательные пределы, эквивалентные, бесконечно малые.
3. Непрерывность функции в точке на множестве. Точки разрыва функции и их классификация.
4. Производная функции в точке. Дифференцируемость функции в точке и на множестве. Геометрический смысл производной, уравнение касательной.
5. Свойства производных, основные правила нахождения производных. Производная сложной функции. Таблица производных.
6. Понятие дифференциала. Геометрический смысл дифференциала. Применение дифференциала к приближенным вычислениям.
7. Возрастающие и убывающие функции. Признаки возрастания и убывания функции на промежутке.
8. Локальные максимум и минимум функции. Необходимое условие экстремума. Достаточные условия экстремума.
9. Выпуклые и вогнутые функции. Точки перегиба. Признаки выпуклости и вогнутости функции на промежутке.
10. Асимптоты функции. Исследование функции и построение графика.
III. Интегральное исчисление
1. Первообразная функция и неопределенный интеграл. Основные свойства неопределенных интегралов.
2. Метод замены переменной в неопределенном интеграле.
3. Метод интегрирования по частям в неопределенном интеграле.
4. Определенный интеграл и его свойства. Геометрический смысл определенного интеграла.
5. Метод замены переменной и интегрирование по частям для вычисления определенного интеграла.
6. Понятие о несобственных интегралах.
IV. Комплексные числа и действия над ними
ЛИТЕРАТУРА
1. Кудрявцев В.А. , Демидович Б.П. Краткий курс высшей математики
2. Шнейдер В.Е. и др. Краткий курс высшей математики
3. Кремер Н.Ш. и др. Высшая математика для экономистов
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Аналитическая геометрия, векторная алгебра
1-10. Даны вершины 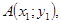
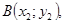
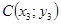 треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A в радианах с точностью до 0,01%; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.
треугольника. Найти: 1) длину стороны AB; 2) внутренний угол A в радианах с точностью до 0,01%; 3) уравнение высоты, проведенной через вершину C; 4) уравнение медианы, проведенной через вершину С; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины С; 7) систему линейных неравенств, определяющую внутреннюю область треугольника. Сделать чертеж.
1. А (1;1), В (7;1), С (4;5)
2. А (1;1), В (7;2), С (4;5)
3. А (1;1), В (7;3), С (4;5)
4. А (1;1), В (7;4), С (4;5)
5. А (1;1), В (7;5), С (4;5)
6. А (1;1), В (8;1), С (4;5)
7. А (1;1), В (8;2), С (4;5)
8. А (1;1), В (8;3), С (4;5)
9. А (1;1), В (8;4), С (4;5)
10. А (1;1), В (8;5), С (4;5)
11-20. Дано уравнение 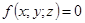 . Требуется:
. Требуется:
1) доказать, что оно является уравнением сферы; 2) найти координаты центра и радиус сферы; 3) составить уравнение плоскости, проходящей через центр сферы и ось Oz; 4) составить уравнения прямой, проходящей через центр сферы и начало координат.
11. 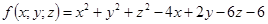
12. 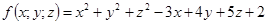
13. 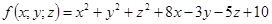
14. 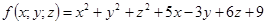
15. 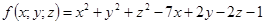
16. 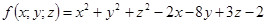
17. 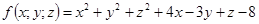
18. 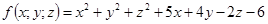
19. 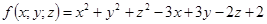
20. 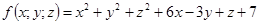
- Введение в анализ. Дифференциальное исчисление
21-30. Найти пределы функций.
21. 1) 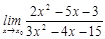 при a)
при a) 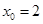 , b)
, b) 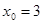 , c)
, c) 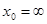 ;
;
2) 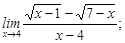 3)
3) 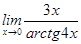 ;
;
4) 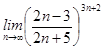
22. 1) 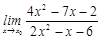 при a)
при a) 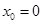 , b)
, b) 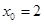 , c)
, c) 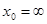 ;
;
2) 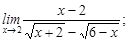 3)
3) 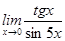 ;
;
4) 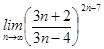
23. 1) 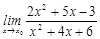 при a)
при a) 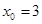 , b)
, b) 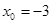 , c)
, c) 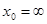 ;
;
2) 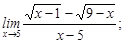 3)
3) 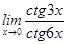 ;
;
4) 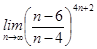
24. 1) 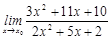 при a)
при a) 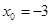 , b)
, b) 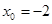 , c)
, c) 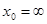 ;
;
2) 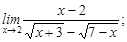 3)
3) 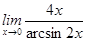 ;
;
4) 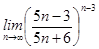
25. 1) 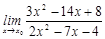 при a)
при a) 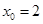 , b)
, b) 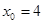 , c)
, c) 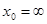 ;
;
2) 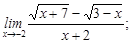 3)
3) 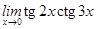 ;
;
4) 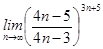
26. 1) 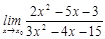 при a)
при a) 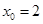 , b)
, b) 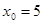 , c)
, c) 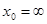 ;
;
2) 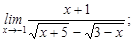 3)
3) 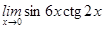 ;
;
4) 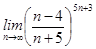


27. 1) 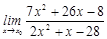 при a)
при a) 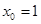 , b)
, b) 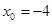 , c)
, c) 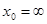 ;
;
2) 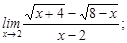 3)
3) 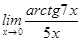 ;
;
4) 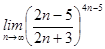
28. 1) 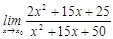 при a)
при a) 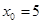 , b)
, b) 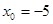 , c)
, c) 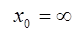




2) 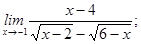
 3)
3) 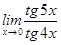
4) 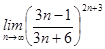
29. 1) 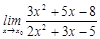 при a)
при a) 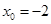 , b)
, b) 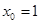 , c)
, c) 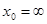 ;
;
2) 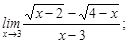 3)
3) 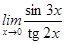 ;
;
4) 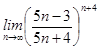
30. 1) 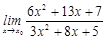 при a)
при a) 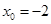 , b)
, b) 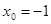 , c)
, c) 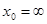 ;
;
2) 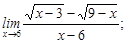 3)
3) 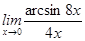 ;
;
4) 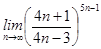
31-40. Найти производные заданных функций.
31. а) 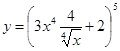 ; б)
; б) 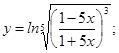
в) 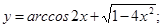 г)
г) 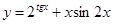 .
.
32. а) 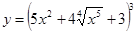 ; б)
; б) 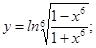
в) 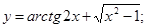 г)
г) 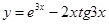 .
.
33. а) 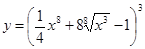 ; б)
; б) 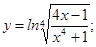
в) 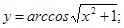 г)
г) 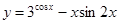 .
.
34. а) 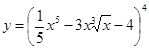 ; б)
; б) 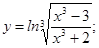
в) 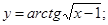 г)
г) 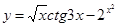 .
.
35. а) 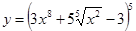 ; б)
; б) 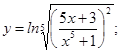
в) 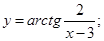 г)
г) 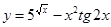 .
.
36. а) 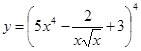 ; б)
; б) 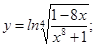
в) 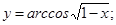 г)
г) 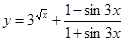 .
.
37. а) 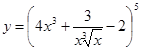 ; б)
; б) 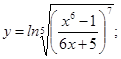
в) 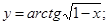 г)
г) 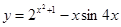 .
.
38. а) 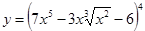 ; б)
; б) 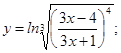
в) 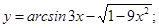 г)
г) 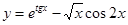 .
.
39. а) 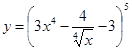 ; б)
; б) 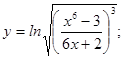
в) 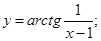 г)
г) 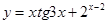 .
.
40. а) 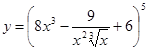 ; б)
; б) 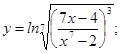
в) 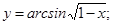 г)
г) 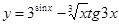 .
.
41-50. Вычислить приближенное значение 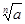 , заменив в точке
, заменив в точке 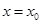 приращение функции
приращение функции 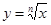 дифференциалом.
дифференциалом.
41. 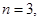
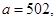
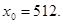
42. 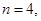
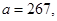
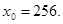
43. 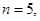
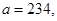
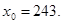
44. 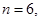
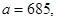
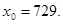
45. 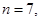
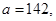
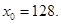
46. 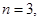
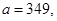
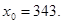
47. 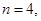
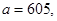
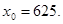
48. 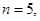
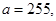
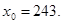
49. 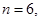
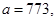
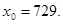
50. 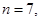
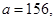
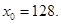
51-60. Исследовать функцию 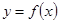 и построить ее график.
и построить ее график.
51. 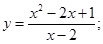 52.
52. 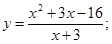
53. 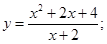 54.
54. 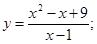
55. 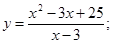 56.
56. 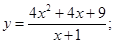
57. 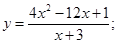 58.
58. 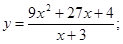
59. 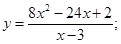 60.
60. 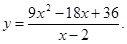
61-70. Найти неопределенные интегралы. Результаты проверить дифференцированием.
61. а) 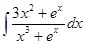 ; б)
; б) 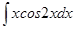 ;
;
62. а) 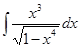 ; б)
; б) 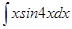 ;
;
63. а) 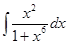 ; б)
; б) 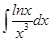 ;
;
64. а) 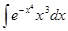 ; б)
; б) 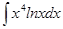 ;
;
65. а) 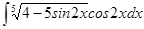 ; б)
; б) 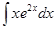 ;
;
66. а) 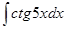 ; б)
; б) 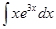 ;
;
67. а) 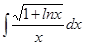 ; б)
; б) 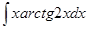 ;
;
68. а) 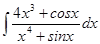 ; б)
; б) 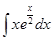 ;
;
69. а) 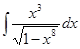 ; б)
; б) 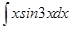 ;
;
70. а) 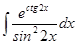 ; б)
; б) 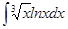 .
.
71-80. Вычислить по формуле Ньютона-Лейбница определенный интеграл 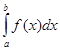 .
.
71. 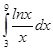 72.
72. 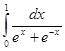 73.
73. 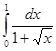
74. 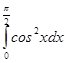 75.
75. 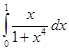 76.
76. 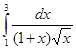
77. 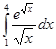 78.
78. 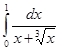 79.
79. 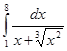
80. 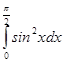
81-90. Вычислить площадь фигуры, ограниченной параболой 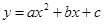 и прямой
и прямой 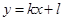 . Сделать чертеж.
. Сделать чертеж.
81. 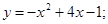
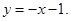
82. 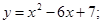
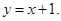
83. 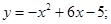
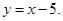
84. 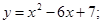
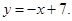
85. 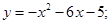
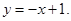
86. 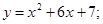
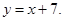
87. 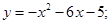
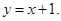
88. 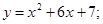
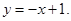
89. 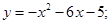
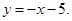
90.