Дифференциальные уравнения относительного движения материальной точки
Имеем инерциальную систему отсчета 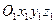 и материальную точку массой
и материальную точку массой 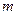 , на которую действуют приложенные силы
, на которую действуют приложенные силы 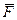 и
и 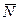 (рис. 49), где
(рис. 49), где 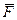 – равнодействующая заданных активных сил;
– равнодействующая заданных активных сил; 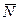 – равнодействующая сил реакций связей. Если
– равнодействующая сил реакций связей. Если 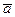 – ускорение точки относительно инерциальной системы отсчета (абсолютное ускорение), то согласно уравнению движения точки в векторной форме имеем
– ускорение точки относительно инерциальной системы отсчета (абсолютное ускорение), то согласно уравнению движения точки в векторной форме имеем
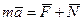 . (134)
. (134)
Если ввести другую, неинерциальную систему отсчета 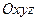 , которая в общем случае может двигаться относительно инерциальной как свободное твердое тело, то по теореме сложения ускорений имеем
, которая в общем случае может двигаться относительно инерциальной как свободное твердое тело, то по теореме сложения ускорений имеем
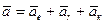 , (135)
, (135)
где 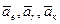 – соответственно переносное, относительное и кориолисово ускорения.
– соответственно переносное, относительное и кориолисово ускорения.
Подставляя значение абсолютного ускорения после переноса слагаемых, кроме 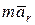 из левой части в правую, получим
из левой части в правую, получим
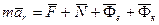 , (136)
, (136)
где 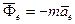 и
и 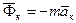 называются соответственно переносной и кориолисовой силами инерции. Получена динамическая теорема Кориолиса, или уравнение относительного движения точки в векторной форме: материальная точка движется относительно неинерциальной системы отсчета так же, как и относительно инерциальной, только к приложенным активным силам и реакциям связей следует добавить переносную и кориолисову силы инерции.
называются соответственно переносной и кориолисовой силами инерции. Получена динамическая теорема Кориолиса, или уравнение относительного движения точки в векторной форме: материальная точка движется относительно неинерциальной системы отсчета так же, как и относительно инерциальной, только к приложенным активным силам и реакциям связей следует добавить переносную и кориолисову силы инерции.
Силы инерции 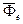 и
и 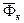 являются поправками на неинерциальность системы отсчета. Для инерциальной системы отсчета они равны нулю, так как в этом случае абсолютное и относительное движения точки совпадают. Переносная и кориолисова силы инерции участвуют в создании относительного ускорения совершенно так же, как и приложенные силы со стороны материальных тел. Но эти силы инерции, по определению приложенных сил классической механики, не приложены к материальной точке, так как не участвуют в создании ее ускорения относительно инерциальной системы отсчета.
являются поправками на неинерциальность системы отсчета. Для инерциальной системы отсчета они равны нулю, так как в этом случае абсолютное и относительное движения точки совпадают. Переносная и кориолисова силы инерции участвуют в создании относительного ускорения совершенно так же, как и приложенные силы со стороны материальных тел. Но эти силы инерции, по определению приложенных сил классической механики, не приложены к материальной точке, так как не участвуют в создании ее ускорения относительно инерциальной системы отсчета.
Если координаты движущейся точки относительно подвижной системы координат 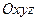 в момент времени
в момент времени 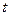 есть
есть 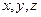 , то в проекциях на подвижные оси координат (136) примет форму:
, то в проекциях на подвижные оси координат (136) примет форму:
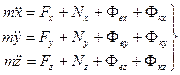 . (136')
. (136')
Это дифференциальные уравнения движения точки относительно подвижной системы координат в проекциях на декартовы подвижные оси координат. Они отличаются от дифференциальных уравнений абсолютного движения относительно инерциальной системы отсчета только наличием поправок на неинерциальность системы отсчета.
Геометрия масс
Центр масс
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит 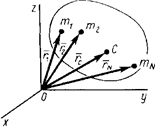 из конечного числа материальных точек
из конечного числа материальных точек 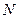 с массами
с массами 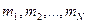 , радиусы-векторы которых
, радиусы-векторы которых 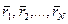 , проведенные из одной и той же точки
, проведенные из одной и той же точки 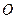 , (рис. 13), то центром масс называется геометрическая точка
, (рис. 13), то центром масс называется геометрическая точка 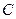 , радиус-вектор которой
, радиус-вектор которой 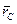 определяется выражением
определяется выражением

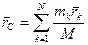 , (137)
, (137)
где 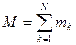 – масса системы. Формулы для декартовых координат центра масс:
– масса системы. Формулы для декартовых координат центра масс:
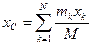 ,
, 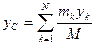 ,
, 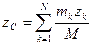 . (137')
. (137')
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 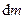 и с изменяющимися от частицы к частице радиусом-вектором
и с изменяющимися от частицы к частице радиусом-вектором 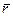 . Суммы в пределе переходят в интегралы. Формулы (137) и (137') принимают форму:
. Суммы в пределе переходят в интегралы. Формулы (137) и (137') принимают форму:
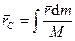 , (138)
, (138)
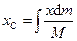 ,
, 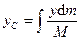 ,
, 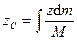 , (138')
, (138')
где 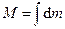 – масса тела.
– масса тела.
Для однородных сплошных тел 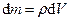 ,
, 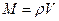 , где
, где 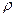 – плотность тела, общая для всех элементарных частиц,
– плотность тела, общая для всех элементарных частиц, 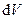 – объем элементарной частицы,
– объем элементарной частицы, 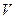 – объем тела.
– объем тела.
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 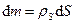 ,
, 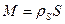 , где
, где 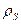 – поверхностная плотность,
– поверхностная плотность, 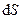 – площадь поверхности элементарной частицы;
– площадь поверхности элементарной частицы; 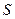 – площадь поверхности.
– площадь поверхности.
Для тонкой проволоки, которую можно принять за отрезок линии, 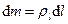 ,
, 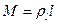 , где
, где 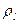 – линейная плотность,
– линейная плотность, 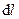 – длина элемента линии;
– длина элемента линии; 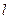 – длина отрезка линии.
– длина отрезка линии.
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
