Узагальнення операцій над множинами, розбиття множини, декартів добуток множин.

Із властивостей комутативності й асоціативності операцій об’єднання випливає, що об’єднання кількох множин можна виконати, послідовно об’єднуючи їх, причому порядок входження множин не впливає на результат, наприклад 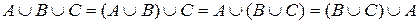. Отже, об’єднання сукупності множин можна подати співвідношенням

.

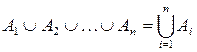Аналогічно на 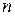множин узагальнюється операція перерізу:

.

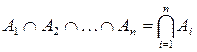Використовуючи узагальнення операцій об’єднання та перерізу на n множин, можна узагальнити також інші співвідношення, наприклад закон де Моргана, який в узагальненому вигляді має вигляд

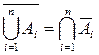і .

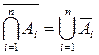Означення 2.8. Сукупність множин 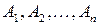називається розбиттям множини , якщо об’єднання всіх цих множин співпадає з множиною , тобто

1.

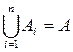
переріз будь-яких двох різних множин 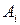і 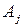є порожньою множиною, тобто

2.

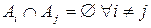
Приклад 2.14. Наведемо приклади розбиття множин:

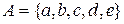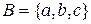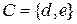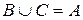Нехай , тоді сукупність множин і є розбиттям множини , тому що , а .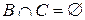

Нехай – множина співробітників деякої фірми. Розбиттям цієї множини є сукупність двох множин – множини чоловіків та множини жінок, які є співробітниками фірми.

Нехай – множина студентів факультету. Сукупність множин 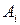, де 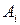– множина студентів 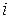-ї групи факультету, є розбиттям множини .

Введемо ще одну операцію над множинами.

Означення 2.9. Прямим (або декартовим) добутком множин і називається множина всіх упорядкованих пар елементів 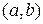, з яких перший належить множині , а другий – множині (позначається ):

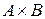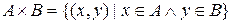
Порядок входження пар може бути будь-яким, але розташування елементів у кожній парі визначається порядком множин, що перемножуються. Тому 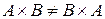, тобто прямий добуток властивості комутативності не має.

Приклад 2.15. Наведемо приклади декартового добутку:

Якщо 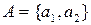, , 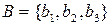тоді

,

.

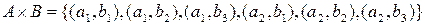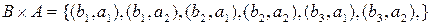Якщо є множина прізвищ 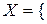Стеценко, Чуйко, Козак} і є множина посад 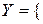старший менеджер, менеджер} філії фірми.

Тоді декартів здобуток 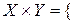(Стеценко, старший менеджер), (Стеценко, менеджер), (Чуйко, старший менеджер), (Чуйко, менеджер), (Козак, старший менеджер), (Козак, менеджер)} є множиною всіх можливих варіантів розподілу прізвищ співробітників за всіма посадами даної філії.

Декартів добуток 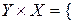(Старший менеджер, Стеценко), (Старший менеджер, Чуйко), (Старший менеджер, Козак), (Менеджер, Стеценко), (Менеджер, Чуйко), (Менеджер, Козак)} є множиною всіх можливих варіантів розподілу посад даної фірми за всіма прізвищами (особами).

Зрозуміло, що в загальному вигляді для двох множин і виконується .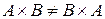

Операція прямого добутку множин узагальнюється на будь-яку їх кількість і записується у вигляді

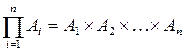
причому елементом прямого добутку 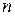множин є впорядкована послідовність із 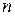елементів ( 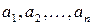), яка називається ще кортежем або вектором завдовжки 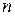, а також впорядкован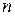ою -кою.

Властивості асоціативності для прямого добутку також не виконуються, але виконується властивість дистрибутивності відносно об’єднання, перерізу і відносного доповнення (різниці):

;

;

.

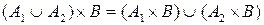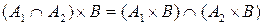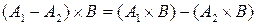Якщо як співмножник декартового добутку 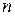-множин використовується одна множина , то це записується так:

.

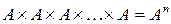Операція декартового добутку відрізняється від операцій, введених раніше, тим, що елементи добутку множин суттєво відрізняються від елементів співмножників і є об’єктами іншої природи. Наприклад, якщо 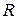– множина дійсних чисел, то декартовий добуток 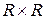– множина всіх точок площини.