Математикалық физика теңдеулеріне қойылатын қосымша шарттар.

Дербес туындылы дифференциалдық теңдеулердің жай дифференциалдық теңдеулер сияқты шексіз көп шешімдері бар болады. Математикалық модель физикалық процесті толық бейнелеу үшін (мысалы, берілген ішектің тербелісін немесе стерженьдегі температураның таралуын) қосымша шарттар қажет. Жай дифференциалдық теңдеулер теориясында олар бастапқы шарттар деп аталады. Нәтижесінде шешімі бар және жалғыз болу теоремасының тұжырымы орындалатын Коши есебін алдық. Дербес туындылы дифференциалдық теңдеу үшін де бастапқы шарттар қою арқылы Коши есебін алуға болады. Математикалық физика теңдеулерінде бастапқа шарттар уақыттың бастапқы моментіндегі (t₀=0) физикалық процестің сипаттамасын анықтайды. Бұл шарттардың жай дифференциалдық теңдеуге қойылатын бастапқа шарттардан өзгешелігі бар. Біріншіден, бастапқы шарттар стационарлы емес процестерге сәйкес келетін теңдеулерге қойылады. Бұлар толқын және жылуөткізгіштік теңдеулері. Екінші, дербес туындылы дифференциалдық теңдеулерге қойылатын Коши есебінің жалғыз шешімі болады, егер сәйкес теңдеулер түзу бойындағы немесе жазықтықтағы немесе кеңістіктегі барлық нүктелер үшін анықталса. Бұған мысал ретінде ақырсыз ішек тербелісіне немесе ақырсыз стержень бойында жылудың таралуына байланысты қойылатын есептерді айтуға болады. Практикада мұндай есептерге процеске ұштарының еш әсері болмайтын өте ұзын ішектің немесе өте ұзын стерженьнің ұштарынан алыс бөліктерінде өтетін процестерді қарастырған жағдайда келеміз. Жалпы жағдайда ұштарынының әсерін есепке алмаған дұрыс емес. Мысалы ұзын сымның ортасынан жай көтеріп жіберіп қойсақ, онда оның бойымен оңға және солға қарай толқын тарайды. Толқындар сымның ұштарына жетіп, шағылысып кейін қайтқан кезде алдындағы сымның ауытқу бейнесі өзгеріске ұшырайды. Сондықтан ұштарының әсерін есепке алмаған, шағылысып кейін қайтатын толқындардың әсерін есепке алмағанмен бірдей.

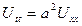
- толқындық теңдеу үшін

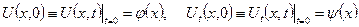(5.5.1)

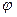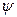түрінде берілетін екі бастапқы шарт қойылады. Бірінші шарт уақыттың бастапқы моментіндегі ішектің ауытқуын, ал екінші шарт уақыттың бастапқы моментіндегі ішек нүктелерінің жылдамдығын сипаттайды. Толқындық теңдеу жазықтықта немесе кеңістікте берілсе, онда олар үшін де екі бастапқы шарт қойылады. Мұндағы және функциялары сәйкесінше екі немесе үш тәуелсіз айнымалыларға байланысты функциялар.

- жылуөткізгіштік теңдеуі үшін

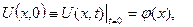(5.5.2)

түрінде берілетін бір бастапқы шарт қойылады. Мұндағы 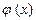стерженьдегі уақыттың бастапқы моментіндегі температураның таралуын сипаттайтын функция. Жазықтықта, кеңістікте берілген жылуөткізгіштік теңдеуі үшін де (5.5.2) сияқты бір бастапқы шарт қойылады. Тек мұндағы 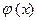функциясы сәйкесінше екі немесе үш тәуелсіз айнымалыға байланысты болады.

5.6. Шекаралық шарттар.Егер ішектің немесе стерженьнің ұзындығы ақырлы болса, онда олардың ұштарының әсерін есепке алмауға болмайды. Мұндай жағдайда бір ғана бастапқы шарт есептің шешімінің жалғыздығын қамтамасыз ете алмайды. Сондықтан ұштарына қосымша шарттар қою керек. Ондай шарттарды шекаралық немесе шектік шарттар деп атайды.

Көбінесе ішек тербелісі үшін негізінен үш түрлі шекаралық шарттар қарастырылады. Олар:

1) бірінші шекаралық шарттар

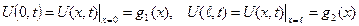(5.6.1)

(5.6.1) шекаралық шарттарының физикалық мағынасы ішектің шеткі нүктелеріндегі тербелісін сипаттайды. Егер 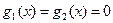болса, онда (5.6.1) шекаралық шарттар ішектің ұштары қатты бекітілгенін білдіреді.

2) екінші шекаралық шарттар

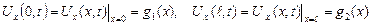(5.6.2)

Мұндай шарттар ішектің ұштары тік бағытта кедергісіз қозғалып отыратын жағдайда қойылады (18-сурет). Өйткені ішектің сол және оң жақ ұштарына әсер ететін күштер 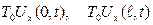өрнектері арқылы анықталады. Сондықтан (5.6.2) шекаралық шарттарының физикалық мағынасы ішектің шеткі нүктелерінде қандай да бір күштердің әсер ететіндігін сипаттайды. Егер 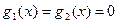болса, онда (5.6.2) шекаралық шарттар ішектің ұштарының бос екендігін білдіреді. Бұл жағдайда ішектің ұштарына ешқандай күштер әсер етпейді.

3) үшінші шекаралық шарттар

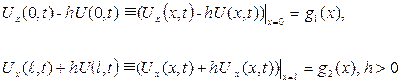(5.6.3)

Мұндағы 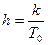тұрақтысының мәні k-серпімділік коэффициентіне байланысты. Көрсетілген жағдайда k-коэффициентінің мәні екі ұшында бірдей. Кері жағдайда ішектің ұштарындағы 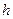- тің мәндері әр түрлі болады. Мұндай шарттар ішектің ұштары серпінді бекітілген жағдайға сәйкес келеді.

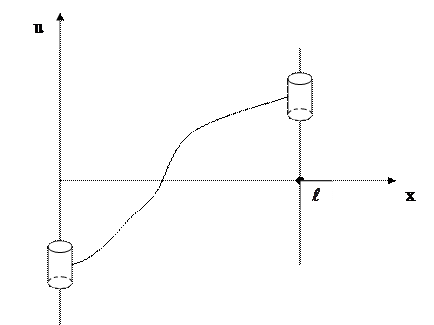
18-сурет

Жылуөткізгіштік теңдеулері үшін қойылатын шекаралық шарттардың түрлері толқындық теңдеулер үшін қойылатын шекаралық шарттардың түрлерімен бірдей, бірақ олардың физикалық мағынасы басқаша. Жылуөткізгіштік теңдеуі үшін (5.6.1) бірінші шекаралық шарттарының физикалық мағынасы стерженьнің ұштарындағы температураны сипаттайды. Егер стерженьнің ұштарындағы температура уақыт өткен сайын өзгермейтін болса, онда 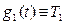және 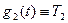болады. Мұндағы 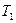және 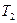тұрақты шамалар. Егер стерженьнің ұштарындағы температураның мәні уақыт өткен сайын нолден өзгермесе, онда 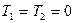болады, жылуөткізгіштік теңдеуі үшін (5.6.2)-екінші шекаралық шарттарының физикалық мағынасы стерженьнің ұштарындағы жылу мөлшерін сипаттайды. Егер 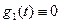және 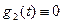болса, онда (5.6.2) шекаралық шарттарының физикалық мағынасы стерженьнің ұштары жылу өткізбейді дегенді білдіреді, яғни стерженьнің ұштарында жылу алмасу болмайды. Егер стерженьнің ұшында сыртқы қоршаған ортамен Ньютон заңы бойынша жылу алмасу орындалады десек, онда стерженьнің ауданы 1-ге тең болатын қимасы арқылы 1 секундта ағып өтетін жылу мөлшеріне тең болатын жылу ағынының тығыздығы стержень мен қоршаған ортаның температураларының айырымына тура пропорционал болады, яғни

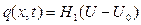
Мұндағы 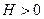сыртқы ортамен жылу алмасу коэффициенті, 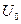сыртқы ортаның температурасы. Сондықтан стерженьнің сол жақ ұшы арқылы өтетін жылу мөлшері - 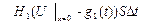. Мұндағы 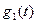стерженьнің сол жақ ұшындағы қоршаған ортаның температурасы. Екінші жағынан стерженьнің теңдеуін қорытып шығару кезінде оның сол жағы арқылы өтетін жылу мөлшері

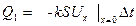тең болатынын көрсеткен болатынбыз. Жылу мөлшерінің сақталу заңын пайдаланып

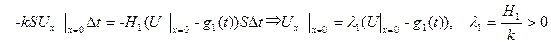(5.6.4)

теңдігі түрінде анықталатын стерженьнің сол жақ ұшында қойылатын үшінші шекаралық шарттың бірінші теңдігіне келеміз. Дәл осы сияқты стерженьнің оң жақ ұшына қойылатын шекаралық шарт

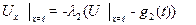(5.6.5)

теңдігі арқылы анықталатындығын көрсету қиын емес. Мұндағы стерженьнің оң жақ ұшындағы қоршаған ортаның температурасы, ал 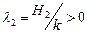. (5.6.4)-(5.6.5) үшінші шекаралық шарттар бірінші және екінші шекаралық шарттарға қарағанда жалпырақ. Мысалы, егер стерженьнің қандай да бір ұшынан жылу алмасу болмаса (яғни сыртқы ортамен жылу алмасу коэффициенті нөлге тең болса), онда біз екінші шекаралық шартқа келеміз. Егер мысалы, сыртқы ортамен жылу алмасу коэффициенті өте үлкен болса, онды (5.6.4) теңдігінен, яғни

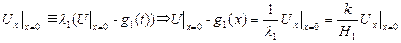
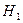шексіздікке ұмтылған кезде 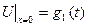бірінші шекаралық шартқа келеміз.

Жазықтықта, кеңістікте қарастылатын жылуөткізгіштік теңдеулері үшін де бір өлшемді жылуөткізгіштік теңдеуіне қойылатын сияқты шекаралық шарттар қойылады. Мұндай жағдайларда облыстың шекарасы жазықтықтағы тұйық Г қисығын немесе кеңістіктегі 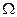тұйық бетін анықтайтын болады. Осыған байланысты екінші және үшінші шекаралық шарттардағы белгісіз функцияның туындысы сәйкесінше жазықтықта Г қисығына сырттай жүргізілген 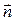нормаль бағытында алынған туындыға, ал кеңістікте 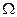бетіне сырттай жүргізілген 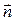бағытында алынған туындыға өзгереді (19-сурет). Мысалы, жазықтағы біртекті бірінші шекаралық шарт 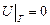, ал кеңістікте 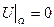түрінде анықталады. Екінші шекаралық шарт жазықтықта 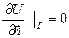, ал кеңістікте 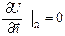теңдігі түрінде анықталады. Әлбетте, бұл шекаралық шарттардың физикалық процестерінің түрлеріне байланысты физикалық мағыналары әр түрлі болады. Мысалы, мембрананың тербелісін қарастырған кезде қойылатын 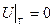шарты мембрананың ұштарының қатты бекітілгенін сипаттайтын болса, онда ол пластинкада жылу таралу процесін қарастырған кезде пластинканың ұштарында нөлдік температура сақталатындығын сипаттайды.

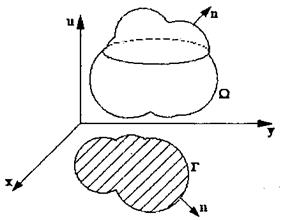
19-сурет

Дәл осы сияқты 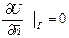және 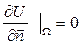сырттай өте ұқсас болғанмен бірінші шарт пластинкада жылу таралу процесін қарастырған кезде пластинканың ұштары жылу өткізбейтіндігін, ал екінші шарт кеңістікте берілген денедегі жылу таралу процесін қарастырған кезде, денені қоршаған беттің жылу өткізбейтіндігін сипаттайтын болады.