Сила гидростатического давления на

Сила гидростатического давления жидкости

На плоскую поверхность.

Задача определения силы гидростатического давления на плоскую поверхность сводится к определению равнодействующих сил гидростатического давления, приложенных к элементарным площадкам, составляющим рассматриваемую поверхность.

Допустим, что плоская стенка, ограничивающая некоторый объем покоящейся жидкости, наклонена к горизонту под некоторым произвольным углом α (рисунок 1)

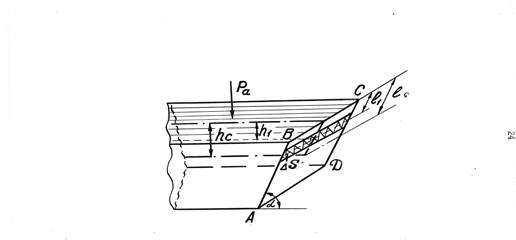Рисунок 1

Условимся, что плоская стенка АБСД полностью соприкасается с жидкостью. Площадь стенки АБСД разобьем на ряд элементарных полосок площадью 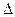S каждая.

Давление в любой точке, лежащей на оси элементарной площадки по основному управлению гидростатистики равно

Р_абс=Р_а+ρgh₁

Ввиду малой ширины 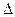S можно считать, что давление такой величины будет во всех ее точках.. Сила давления на всю элементарную площадку 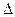S будет

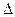Р_абс=(Р_а+ρgh₁) 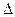S

Для нахождения силы гидростатического давления на всю смоченную поверхность стенки АБСД просуммируем элементарные силы давления

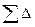Р_абс= Р_абс= 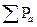∆S+ρgh₁ 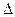S

Р_абс=Р_а∑∆S+ρg∑h₁· 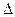S

Учитывая, что

∑∆S=S и h₁=ℓ₁ Sinα

Р_абс=Р_аS+ρg∑ℓ₁ Sinα ∆S=

Получим

=Р_аS+ρg Sinα ∑ℓ₁ ∆S

∑ℓ₁∆S –есть, как известно из механики, статический момент площади смоченной поверхности относительно линии уреза жидкости (линии БС), равным

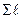₁ΔS= S 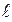_с

(площади, умноженной на расстояние до центра тяжести площади).

Тогда Р_абс= Р_аS+ ρq Sinα S 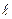_с

а 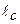Sinα = h_с и следовательно

Р_абс = Р_аS + ρq h_с S

Окончательно

Р_абс = (Р_а + ρq h_с) S

Так как угол α был взят произвольно, то найденное выражение действительно для любого положения плоской стенки – от горизонтального до вертикального.

Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести смоченной поверхности на площадь этой поверхности.

Для технических расчетов обычно определяют не абсолютное давление, а избыточное давление на поверхности, так как действие атмосферного давления на свободную поверхность жидкости и на внешнюю не смоченную поверхность взаимно уравновешиваются.

Тогда Р_изб = ρq h_с S

Для определения силы гидростатического давления жидкости на плоскую поверхность необходимо знать кроме величины и направления силы, также точку приложения этой силы – так называемый центр давления.

Положение центра давления необходимо знать при проектировании различных гидротехнических сооружений. Для плоских геометрических фигур, имеющих вертикальную ось симметрии, центр давления находится на оси и всегда расположен ниже центра тяжести.

Центр давления может быть вычислен по формуле

,

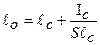где 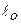- расстояние до центра давления всей площади поверхности;

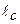- расстояние в плоскости поверхности до центра тяжести;

S - площадь поверхности;

I_с - момент инерции относительно оси, проходящей через центр тяжести.

Расчетные параметры плоских поверхностей различной конфигурации, часто встречающихся в практике, приведены в таблице 1.

Таблица 1

Расчетные параметры плоских поверхностей

различных конфигураций

Конфигурация стенки	hс	ℓ0	Ѕ	Р	Iс
Треугольник	h/ч	2/3h	h b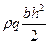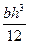
Равнобедренный треугольник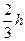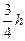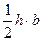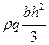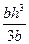
Трапеция					-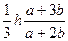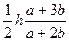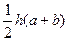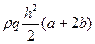
Круг	r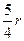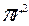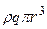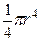
Полукруг					-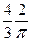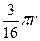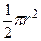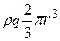

h_с – координата центра тяжести;

ℓ₀ – координаты центра давления;

Ѕ - площадь фигуры;

Р - сила давления на плоскую поверхность;

I_с - момент инерции;

h - высота поверхности;

b - ширина основания поверхности;

а, b – размер основной трапеции;

r - радиус круга;

Нами выведена формула для определения силы гидростатического давления на плоскую поверхность. Как было отмечено, что эта формула справедлива для любого наклона плоской поверхности. Представим себе, что плоская поверхность расположена горизонтально, т.е. ее можно представить, как дно вертикального резервуара (рисунок 2) площадью .

Как определить силу гидростатического давления на дно резервуара, если высота налива горючего плотностью ρ составляет Н? (проблемный вопрос)

Формула для определения Р_изб для плоской поверхности Р_изб = ρq h_с S

Так как все точки дна испытывают одинаковое гидростатическое давление, зависящее от высоты налива жидкости в резервуар Р_изб = ρqН, тогда давление на всю площадь дна резервуара будет равна

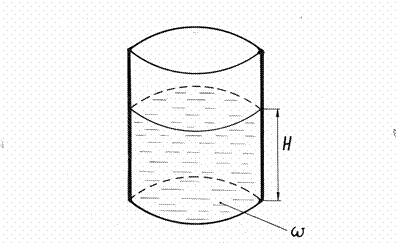Р_изб = ρqНS.

Рисунок 2

Вывод по первому вопросу вопросу

Выведена формула для определения гидростатического давления на плоскую стенку, что позволяет определять толщину стенок и днища резервуаров прямоугольной формы

Сила гидростатического давления на