Умножение матрицы на число - процесс, заключающийся в умножении числа на каждый элемент матрицы

Свойства матриц

Итак, что мы можем сказать про матрицы? Матрица – это таблица чисел. Что мы можем делать с матрицами?

1. Если есть две (m×n) матрицы А и В, то можно найти сумму этих матриц: С=А+В, где С – матрица (m×n).

2. Если есть (m×n)матрица А и число λ, то можно найти (m×n) матрицу В=λА

3. Для каждой (m×n) матрицы А существует свою “нулевая” матрица О, все элементы которой равны нулю.

4. Разностью двух матриц называется матрица А+(-В), которая записывается следующим образом А-В

Матрицей называется прямоугольная таблица чисел, содержащая m строкодинаковой длины.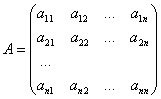 Матрицы равны между собой, если равны все их соответствующие элементы.Матрица, у которой число строк и столбцов равно – называется квадратной.Матрица, все элементы которой, кроме элементов главной диагонали равны нулю,называется диагональной.Диагональная матрица, у которой все элементы главной диагонали равны 1,называется единичной. Обозначается буквой Е.Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю,называется треугольной.Матрица, у которой все элементы равны нулю, называется нулевой.Операция умножения возможна, если количество столбцов первой матрицы равноколичеству строк другой матрицы.Для нахождения определителя более высокого порядка, матрицу приводят ктреугольному виду и считают произведение элементов на главной диагонали. Свойства:1. Определитель не изменится, если его строки заменить столбцами, инаоборот.2. При перестановке двух параллельных рядов определитель меняет знак.3. Определитель, имеющий два одинаковых или пропорциональных ряда,равен нулю.4. Общий множитель элементов можно вынести за знак определителя.5. Если элементы какого-либо ряда представляют собой сумму элементов,то определитель может быть разложен на сумму двух соответствующихопределителей.6. Определитель не изменится, если прибавим ко всем элементам рядаматрицы соответствующих элементов параллельного ряда, умноженных на одно итоже число.7. Определитель равен сумме элементов, умноженных на соответствующееим алгебраическое дополнение.8. Сумма произведения элементов одного ряда на алгебраическиедополнения параллельного ряда равна нулю.

5 вопрос)

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Минор А матрицы A ― определитель квадратной матрицы порядка k (который называется также порядком этого минора), элементы которой стоят в матрице A на пересечении строк с номерами 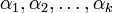и столбцов с номерами .

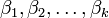Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые kстолбцов ― угловым или ведущим главным.

Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.

Если в любой матрице A взять произвольные k строк и столбцов и составить из элементов этих строк и столбцов подматрицу размера k на k, то такая подматрица называется минором матрицы A. Количество строк и столбцов в наибольшем таком миноре, отличном от нуля, называется рангом матрицы.

6 вопрос)

Вычисление ранга матрицы

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

4 вопрос)

Определитель, или детерминант — одна из важнейших характеристик квадратных матриц. Определитель матрицы размера n × n равен ориентированному n-мерному объёму параллелепипеда, натянутого на её векторы-строки (или столбцы).

Для матрицы n × n определитель выражается в виде многочлена степени N от элементов матрицы который представляет собой сумму произведений элементов матрицы со всевозможными комбинациями различающихся номеров строк и столбцов, причём в каждом из произведений элемент из любой строки и любого столбца ровно один. Каждому произведению приписывается знак плюс или минус в зависимости от чётности перестановки номеров.

Если элементами матрицы являются числа, то определитель — это тоже число. В общем случае определитель может быть функциональным, векторным и т.п., то есть, представлять собой иные выражения, составленные из элементов.

7 вопрос)

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

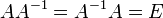
9 вопрос)

1. Сложение и вычитание матриц:

Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицыодинаковых размеров

, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:

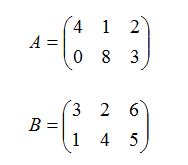
Сумма двух матриц:

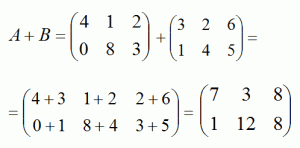
Разность двух матриц:

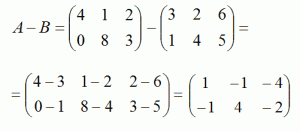
2. Умножение матрицы на число:

Умножение матрицы на число - процесс, заключающийся в умножении числа на каждый элемент матрицы.

Например, пусть дана матрица А:

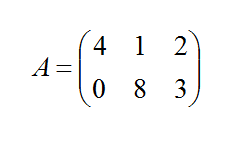
Умножим число 3 на матрицу А:

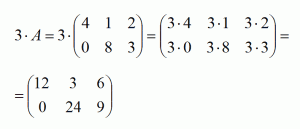
3. Умножение двух матриц:

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.

Можно представить все это в виде схемы:

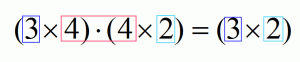
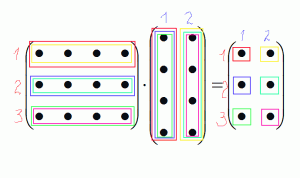
После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.

Посмотрим как это выглядит на схеме:

Посмотрим как это выглядит на примере:

Даны две матрицы:

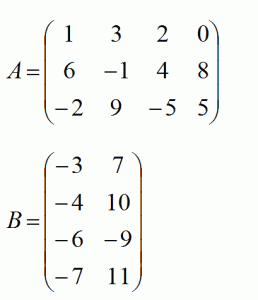
Найдем произведение этих матриц:

4. Деление матриц:

Деление матриц - действие над матрицами, которое в этом понятии не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней:

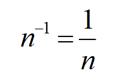
Согласно этому свойству разделим матрицу А на матрицу В:

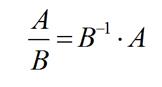
В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.

Задачу об обратной матрице рассмотрим в следующей статье.

Итак мы рассмотрели действия над матрицами.

12 вопрос)