Метод решения неравенства на промежутках

Разбиение ОДЗ неизвестной неравенства на промежутки позволяет упростить некоторые неравенства. Решение неравенства рассматривают отдельно на каждом промежутке.

Предложим еще один способ решения примеров 7 и 10.

Пример 11. (ЕГЭ-2011). Решить неравенство

.

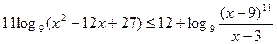Решение. Выше уже было установлено, что обе части неравенства определены при .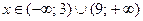

Рассмотрим два случая.

1. Пусть 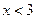. Тогда

,

.

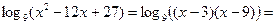
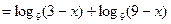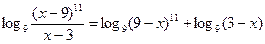В этом случае неравенство примет следующий вид:

. .

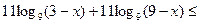
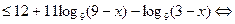
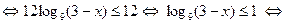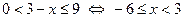2. Пусть 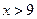. Тогда

,

.

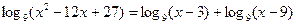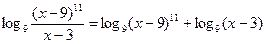В этом случае неравенство примет следующий вид:

.

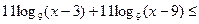
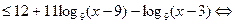
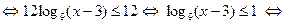
Учитывая, что 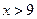, имеем .

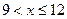Объединяя найденные решения, получаем значения .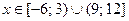

Ответ: .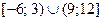

Пример 12 (ЕГЭ 2011). Решить неравенство

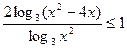
Решение. Неравенство определено при условиях

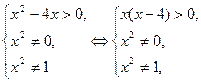
то есть при всех значениях .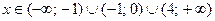

Приведем данное неравенство к виду

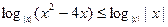
и рассмотрим три случая.

Если значения , то . То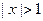гда получаем неравенство 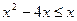или 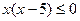с решениями 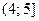для рассматриваемого случая.

Рассмотрим значения 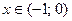, тогда 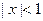. Имеем неравенство или 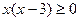, с решениями .

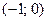Пусть значения 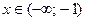. При 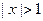от логарифмического неравенства придем к неравенству 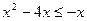или 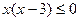не имеющих решений на рассматриваемом промежутке. В итоге получаем решение данного неравенства: .

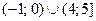Замечание. Еще один вариант рассмотрения решения данного неравенства при разбиении области его определения на промежутки – заменить данное неравенство следующей равносильной совокупностью систем:

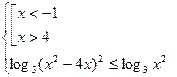
и

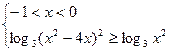
Ответ: .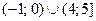

Пример 13 (ЕГЭ 2010). Решить неравенство

.

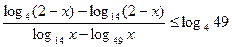Решение. Значения 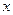, при которых определены обе части неравенства, задаются условиями

.

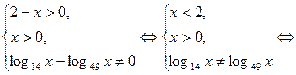
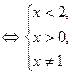
Для таких 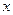преобразуем левую часть исходного неравенства

.

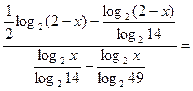
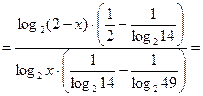
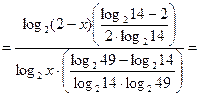
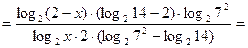
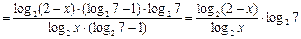Получаем

.

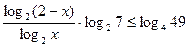
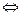
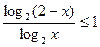Рассмотрим два случая.

1. Пусть 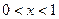. Тогда 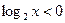, поэтому последнее неравенство равносильно неравенству .

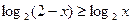Отсюда 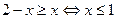. Получаем на рассматриваемом промежутке .

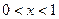2. Пусть 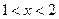. Тогда 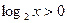, поэтому последнее неравенство равносильно неравенству .

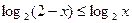Отсюда 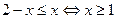. Получаем на рассматриваемом промежутке .

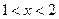Объединяя полученные решения, имеем значения .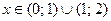

Ответ: .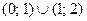

Метод замены

Логарифмическое неравенство может быть упрощено и сведено к простейшему логарифмическому использованием надлежащей замены. Рассмотрим несколько примеров.

Пример 14. (МИОО,апрель 2011).Решить неравенство

.

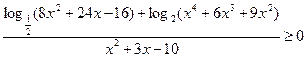Решение. Запишем неравенство в следующей форме:

.

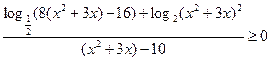Пусть 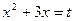. Тогда неравенство примет вид

.

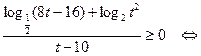
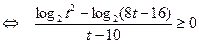Последнее неравенство равносильно совокупности двух систем:

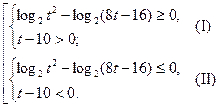
Рассмотрим систему ( 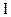). Решим первое неравенство этой системы.

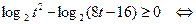
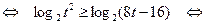
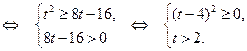
Отсюда получаем 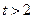. С учетом второго неравенства системы (I) 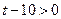или , получаем решение (I) .

Рассмотрим систему (II). Решим ее первое неравенство.

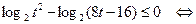
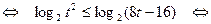
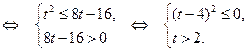
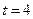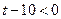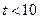Отсюда . С учетом второго неравенства системы (II) или , получаем решение (II) .

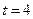Объединяя решения (I) и (II), получим решение исходного неравенства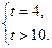

Выполняя обратную замену, имеем

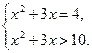
Отсюда получаем .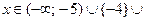

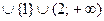Ответ: .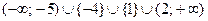

Пример 15. (ЕГЭ 2010).Решить неравенство

.

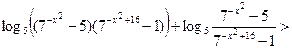
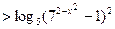Решение. В соответствии с определением логарифма, входящие в неравенство выражения имеют смысл при выполнении условий:

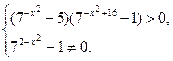
Сделаем замену 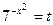. Так как неравенство 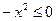выполняется при всех 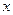, то по свойству степени с основанием больше единицы получаем 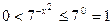. Отсюда 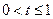. С учетом последнего неравенства, запишем полученную выше систему

.

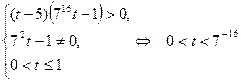Исходное неравенство с переменной 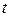будет иметь вид

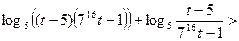
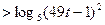,где .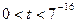

Используя свойство логарифма (при допустимых значениях переменной сумма логарифмов с одинаковым основанием равна логарифму произведения), получим

,

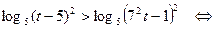
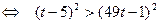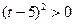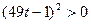так как и при 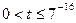. Решим последнее неравенство:

.

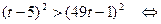
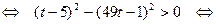
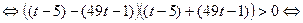
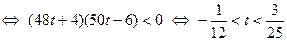С учетом ограничения на 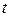получаем 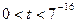. Выполнив обратную замену, имеем 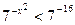. Отсюда

.

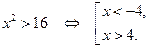Ответ: .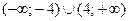

Пример 16. (МИОО, 2011).Решите неравенство

.

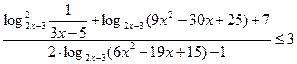Решение. Так как

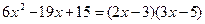
и в соответствии с определение логарифма 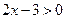, 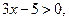то данное неравенство равносильно неравенству

.

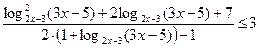Пусть 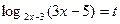. Тогда получаем 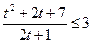, т.е. 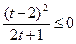. Решение последнего неравенства есть множество .

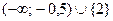Выполняя обратную замену, получаем

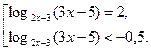
Решим уравнение совокупности:

.

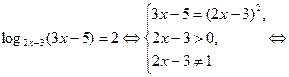
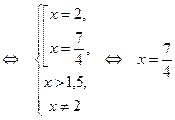Решим неравенство совокупности:

.

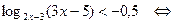
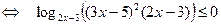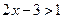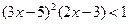В последнем неравенстве при , т.е. , получаем , что неверно, так как в этом случае и .

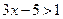При 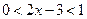, т.е. при 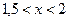, получаем 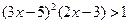, что также невозможно, так как 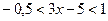и в этом случае произведение .

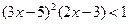Ответ: .

Пример 17. (МИОО,апрель 2011).Решить неравенство

.

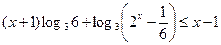Решение. Область определения данного неравенства задается условием 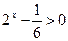. Отсюда, логарифмируя по основанию 2 обе части неравенства 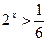, получаем .

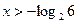Преобразуем левую часть исходного неравенства:

.

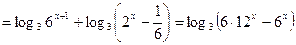Получаем

.

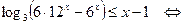
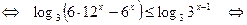
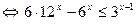Деля в последнем неравенстве на 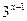, получим .

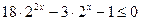Пусть 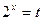, где 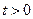. Тогда, решая квадратичное неравенство 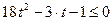, получим 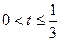. Выполняя обратную замену, отсюда получаем 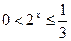, т.е. .

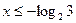Учитывая условие 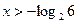, запишем ответ: .

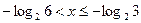Ответ: 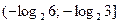.