Понятие алгебраического дополнения

МАТРИЦЫ

Прямоугольная таблица чисел

,

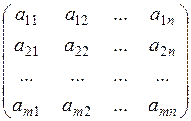содержащая 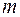строк и 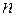столбцов, называется матрицей размеров 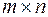. Числа 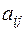называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй – номер столбца, в которых расположен этот элемент. Часто вместо подробной записи употребляют сокращенную: 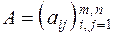или даже 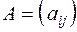. Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной порядка 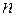. Диагональ 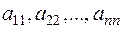квадратной матрицы называется главной диагональю, а диагональ 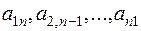– побочной диагональю.

Среди квадратных матриц одного и того же порядка (например, порядка 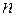, т.е. размеров 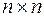) важную роль играет матрица вида

,

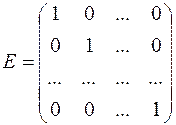которую называют единичной матрицей.

Пример 1. Матрица

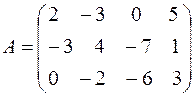
имеет размеры 3×4, например, элементы , .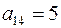

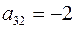Матрица

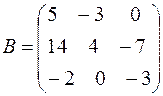
является квадратной порядка 3. Элементы 5, 4, –3 образуют главную диагональ, а элементы 0, 4, –2 матрицы – побочную диагональ.

Умножение матрицы на число. Для того чтобы умножить матрицу 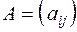на число 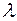, нужно каждый элемент матрицы умножить на это число: .

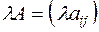Сложение матриц. Складывать можно только матрицы с одинаковым числом строк и столбцов, т.е. матрицы одинаковых размеров. Суммой матриц 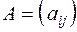и 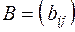называется матрица 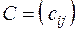, элементы которой равны суммам соответствующих элементов матриц и 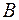, т.е. 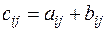для любых индексов , .

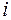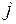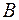Умножение матриц. Произведение матрицы на матрицу (обозначается 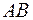) определено только в том случае, когда число столбцов матрицы равно числу строк матрицы 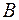. В результате умножения получим матрицу 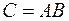, у которой столько же строк, сколько их в матрице , и столько же столбцов, сколько их в матрице 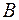. Для удобства запоминания запишем это кратко:

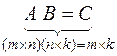
Есл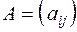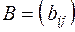и , и 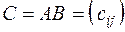, то элементы 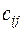определяются следующим образом:

,

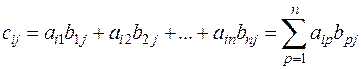где .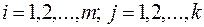

Это правило можно сформулировать и словесно: элемент 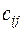, стоящий на пересечении 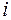-й строки и 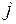-го столбца матрицы 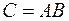, равен сумме попарных произведений соответствующих элементов 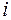-й строки матрицы и 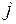-го столбца матрицы 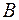. Другими словами, элемент 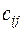является результатом скалярного произведения 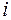-й вектор-строки и 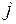-го вектор-столбца.

Пример 2. Выполнить действия:

.

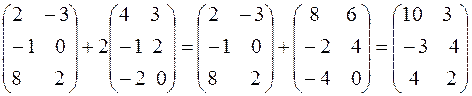Пример 3. Перемножить матрицы:

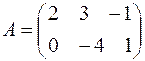и .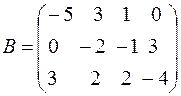

Матрица имеет размерность 2×3, матрица 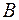имеет размерность 3×4, значит, матрицы можно перемножить. Размерность матрицы произведения С– 2×4. Чтобы получить первый элемент матрицы С перемножим элементы первой строки матрицы А на соответствующие элементы первого столбца матрицы В. Элементы 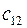, , 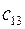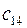получим умножением элементов первой строки матрицы А на соответствующие элементы второго, третьего, четвертого столбцов матрицы В.

2 3 –1 2 3 –1 2 3 –1 2 3 –1

–5 0 3 3 –2 21 –1 20 3 –4

–10+0– 3= –13 6 – 6 – 2 =–2 2 – 3 – 2= –3 0 + 9 + 4=13.

Элементы 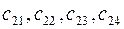получим умножением элементов второй строки матрицы А на соответствующие элементы первого, второго, третьего, четвертого столбцов матрицы В.

0 –4 1 0 –4 1 0 –4 1 0 –4 1

–5 0 33 –2 21 –1 20 3 –4

0 – 0 + 3=3 0 + 8 + 2=10 0 + 4 + 2 =6 0 – 12 – 4= –16

Итак, матрица произведения С имеет вид:

.

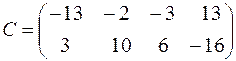ОПРЕДЕЛИТЕЛИ

Каждой квадратной матрице может быть поставлено в соответствие некоторое число, вычисляемое по определенному правилу с помощью элементов матрицы. Такое число называют определителем (или детерминантом) матрицы и обозначают символом 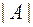или 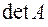. При этом порядком определителя называют порядок соответствующей матрицы.

Правила вычисления определителей 2-го и 3-го порядков легко выписать:

,

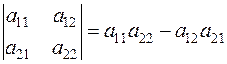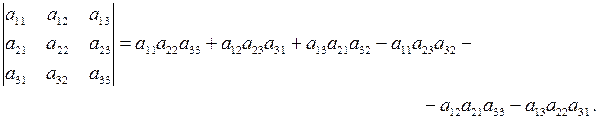
Последнюю формулу, несмотря на внешнюю сложность записи, нетрудно запомнить. Если соединить линией каждые три элемента определителя, произведение которых входит в правую часть последней формулы со знаком « 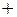», то получим легко запоминающуюся схему 1. Аналогично для произведений, входящих со знаком «–», имеем схему 2.

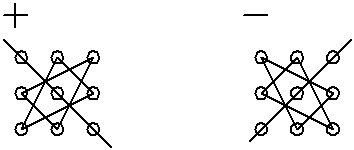Схема 1 Схема 2

Это правило вычисления определителей 3-го порядка называется правилом треугольников.

Пример 4. Вычислить определитель матрицы второго порядка

.

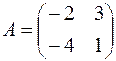Имеем det A=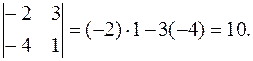

Пример 5. Вычислить определитель матрицы третьего порядка

.

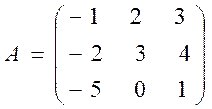Получаем det A=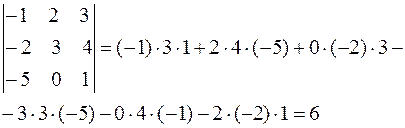

ПОНЯТИЕ АЛГЕБРАИЧЕСКОГО ДОПОЛНЕНИЯ

Пусть дана матрица 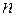-го порядка. Минором любого элемента 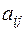называют определитель порядка 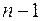, соответствующий той матрице, которая получается из матрицы в результате вычеркивания 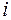-й строки и 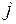-го столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент 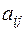). Минор элемента 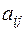будем обозначать символом .

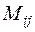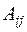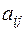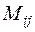Алгебраическим дополнением элемента матрицы называют минор этого элемента, умноженный на 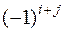, т.е.

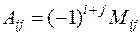. (1)

Пример 6.Задана матрица

.

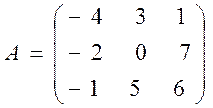Найти минор элемента 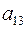, алгебраическое дополнение элемента .

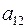Минором элемента 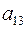является определитель матрицы, полученной вычеркиванием из матрицы А первой строки и третьего столбца:

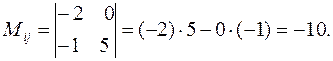
Алгебраическое дополнение элемента 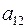найдем по формуле:

.

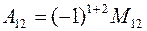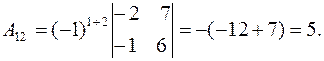
ОБРАТНАЯ МАТРИЦА

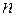Определение. Пусть – квадратная матрица -го порядка. Квадратная матрица 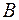(того же порядка 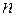) называется обратной для , если

.

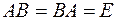Матрицу, обратную к матрице , принято обозначать символом .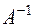

Теорема. Если 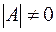, то для нее существует обратная матрица 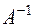, которая вычисляется по формуле

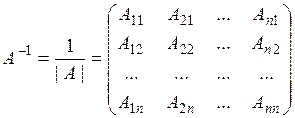, (2)

где 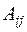– алгебраическое дополнение для элемента 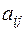матрицы .

(Без доказательства)

Пример 7.Найти матрицу, обратную для матрицы

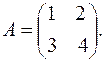
Вычислим определитель матрицы:

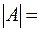
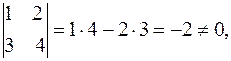следовательно, обратная матрица существует. Формула (2) для матрицы второго порядка имеет вид

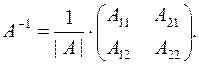(3)

Алгебраические дополнения 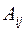найдем по формуле (3):

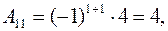
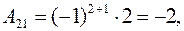
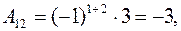
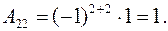
Подставляя полученные значения алгебраических дополнений и определителя матрицы в формулу (3), получаем

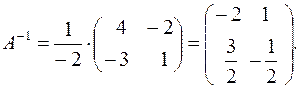
Чтобы проверить, правильно ли найдена обратная матрица, умножим полученную матрицу на исходную.

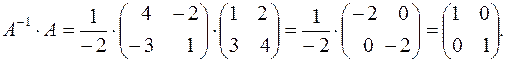
В результате умножения получилась единичная матрица, значит, обратная матрица найдена правильно.

Пример 8.Найти матрицу, обратную для матрицы

А=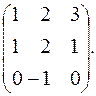

Вычислим определитель матрицы по правилу треугольников:

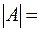detA=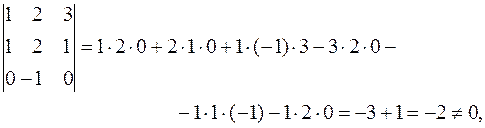

следовательно, обратная матрица существует.

Для матрицы третьего порядка, каковой является заданная матрица, формула (2) вычисления обратной матрицы принимает вид:

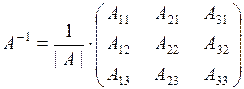. (4)

Найдем алгебраические дополнения по формуле (4).

,

, ,

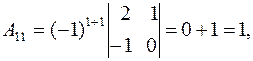
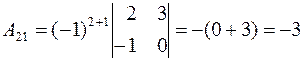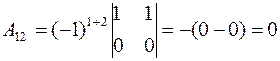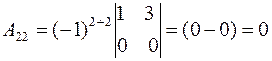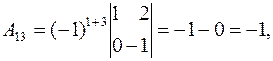
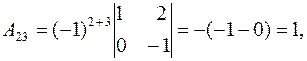
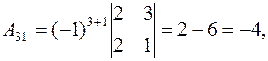
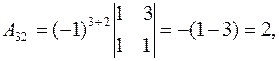
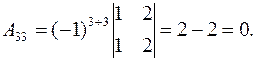
Подставляя полученные значения алгебраических дополнений и определителя матрицы в формулу (4), получаем

.

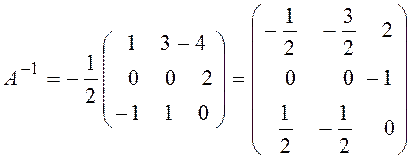Сделаем проверку:

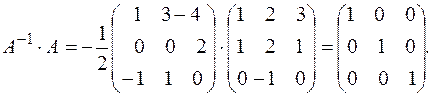
Следовательно, обратная матрица найдена верно.

РАНГ МАТРИЦЫ

Ранее для квадратной матрицы 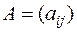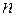-го порядка было введено понятие минора 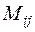элемента 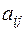. Напомним, что так был назван определитель порядка 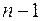, полученный из определителя 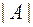вычеркиванием 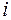-й строки и 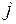-го столбца.

Введем теперь общее понятие минора. Рассмотрим некоторую, не обязательно квадратную матрицу . Выберем какие-нибудь 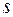номеров строк 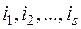и 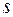номеров столбцов .

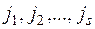Определение. Минором порядка 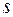матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка 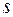, образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число

.

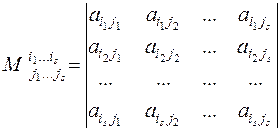Каждая матрица имеет столько миноров данного порядка 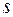, сколькими способами можно выбрать номера строк 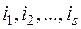и столбцов .

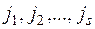Определение. В матрице размеров 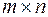минор порядка 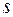называется базисным, если он отличен от нуля, а все миноры порядка 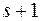равны нулю или миноров порядка 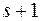у матрицы вообще нет.

Ясно, что в матрице может быть несколько разных базисных миноров, но все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка 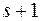равны нулю, то равны нулю и все миноры порядка 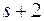, а, следовательно, и всех бόльших порядков.

Определение. Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.

Ранг матрицы будем обозначать символом 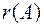. Из определения ранга следует, что для матрицы размеров 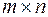справедливо соотношение .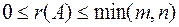