Ламинарное прямолинейное установившееся движение вязких жидкостей в круглых трубах
Жидкость считаем несжимаемой ( 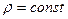 ), движение установившемся
), движение установившемся 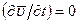 .
.
Рассмотрим случай, когда траектории всех частиц будут строго прямолинейными и параллельными между собой. Направим ось Oх по оси трубы. Тогда 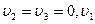 положим равным
положим равным 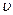 [10].
[10].
Из уравнения неразрывности получим, что 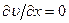 , то есть
, то есть 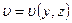 .
.
Вследствие этих предположений квадратичные члены инерции выпадают из полных уравнений движения. Из–за симметрии течения относительно оси трубы 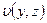 определяется не самими координатами y и z, а лишь их комбинацией
определяется не самими координатами y и z, а лишь их комбинацией 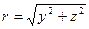 , являющейся расстоянием точки сечения трубы от оси, то есть
, являющейся расстоянием точки сечения трубы от оси, то есть 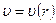 .
.
В общем случае одномерного течения ньютоновских и неньютоновских вязких жидкостей
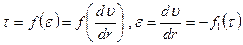 (3.1)
(3.1)
где 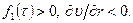
Для вязкой ньютоновской жидкости
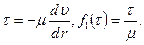
Для степенной жидкости
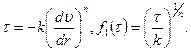
Для вязкопластичной жидкости
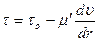 или
или 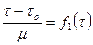
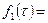 0 при
0 при 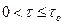
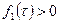 при
при 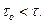
Распределение касательного напряжения по радиусу.
Выделим внутри жидкости, движущейся по трубе, цилиндр радиуса r и длиной l (рис. 3.1).
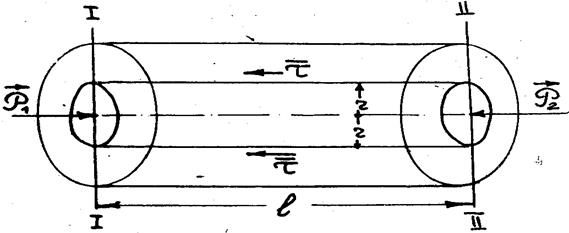
Рис. 3.1.
Рассмотрим силы, действующие на выделенный цилиндр. В сечении (1 – 1) действует сила давления P1 = p1πr2, в сечении (2 – 2) – сила Р2 = p2πr2; p1 и p2 давления в сечениях (1 – 1) и (2 – 2). На боковую поверхность цилиндра действует сила трения Т = 2πrlτ, где τ – среднее по периметру касательное напряжение. Кроме того, на выделенный объем жидкости действует сила инерции, равная массе жидкости выделенного объема М, умноженной на ускорение движения его центра тяжести ас со знаком "минус".
Уравнение равновесия всех сил в проекции на ось трубы имеет вид:
(p1 –p2) πr2 - 2πrlτ + (-M ас) = 0. (3.2)
Так как движение установившееся, то 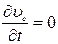 , а из уравнения неразрывности следует, что
, а из уравнения неразрывности следует, что 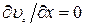 .
.
Следовательно,
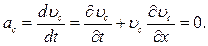
Из (3.2) получим, что
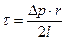 (Δp = p1 - p2) (3.3)
(Δp = p1 - p2) (3.3)
Обозначим через 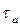 среднее по периметру трубы напряжение трения. Тогда
среднее по периметру трубы напряжение трения. Тогда
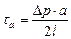 (3.4)
(3.4)
где а — радиус трубы. Из (3.3) и (3.4) следует
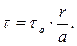 (3.5)
(3.5)
Соотношение (3.5) показывает линейность связи между касательным напряжением и радиусом сечения трубы.
Распределение скорости в сечении трубы.
Запишем реологическое уравнение (3.1) в виде:
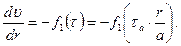 (3.6)
(3.6)
Проинтегрируем (3.6) по r от а до r. При r = а, скорость считаем равной нулю (условие прилипания):
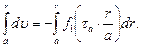 (3.7)
(3.7)
Имеем
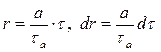 (3.8)
(3.8)
при r = а, τ = τа; при r = r; τ = τ. Тогда из (3.7) получим
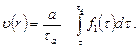 (3.9)
(3.9)
Таким образом, мы получили формулу, дающую закон распределения скорости жидкости по радиусу при любом виде функции f1(τ).
Определение расхода жидкости.
Для определения расхода жидкости найдем элементарный объемный расход через сечение, заключенное между концентрическими окружностями с радиусами r и r+dr.
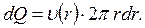
Чтобы определить полный расход, проинтегрируем полученное соотношение
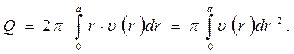 (3.10)
(3.10)
Интегрируем (3.10) по частям:
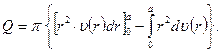
Учитывая, что
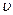 (a) = 0 и dυ = -f1(τ)dr
(a) = 0 и dυ = -f1(τ)dr
и пользуясь формулами (3.8), получим
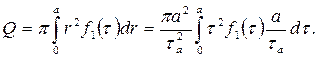
Или окончательно
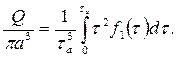 (3.11)
(3.11)
Итак, определен расход жидкости в трубе при любом виде функции f1(τ). Рассмотрим несколько примеров.
