Однофакторный дисперсионный анализ по сменам

В исследуемом производственном примере существует четыре уровня р = 3 (1 смена, 2 смена, 3 смена), необходимые для разбиения общей совокупности наблюдений. Пусть для каждого уровня было проведено число наблюдений n = 30. Таким образом, общее число наблюдений N = р · 30 = 90. Определяем степени свободы по формуле
ν₁ = p – 1 = 2, где ν₂ = N – p = 87 (табл. 5.1).

Таблица 5.1

Показатели	Расчетные формулы	Количество переработанной руды	Содержание S в конц.	Содержание Ме в хвост.	Содержание Ме в сульф.
Различия между уровнями		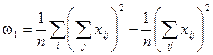104737,267	0,017	0,004	0,11
Различия внутри уровней		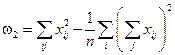378968,733	1,844	0,120	6,80
Сумма	ω = ω1 + ω2	483706,000	1,862	0,123	6,92
Межгрупповая оценка дисперсии	σ12 = ω1 / p – 1	52368,633	0,01	0,0018	0,02
Внутригрупповая оценка дисперсии	σ22 = ω2 / N – p	4355,962	0,02	0,0014	0,03
Расчетное значение критерия Фишера	Fрасч	12,022	0,41	1,29	0,70
Табличное значение критерия Фишера	Fтабл	2,76	2,76	2,76	2,70
%		21,65%	0,94%	2,87%	1,67%

Расчетные данные таблицы 5.1 показывают, что только для количества переработанной руды F_расч > F_табл. Отсюда можно сделать вывод о том, что гипотеза о существенном влияние смены на количество переработанной руды подтвердилась, вероятность составляет 21,65 %. На остальные параметры гипотеза о влиянии смены не подтверждается. При разработке автоматизированных систем управления технологическим процессом (АСУТП) необходимо учитывать это обстоятельство.

Однофакторный дисперсионный анализ по декадам

Существует четыре уровня р3 (1 декада, 2 декада, 3 декада), необходимых для разбиения общей совокупности. Для каждого уровня было проведено наблюдений n = 10, значит, общее число наблюдений N = р · 10= 30. Определяем степени свободы по формулам ν₁ = p – 1 = 2; ν₂ = N – p = 27 (табл. 5.2).

По данным табл. 5.2 видно, что наблюдения содержания металла в сульфате F_расч. < F_табл. Отсюда можно сделать вывод о том, что гипотеза о существенном влиянии декады только на этот параметр подтвердилась, вероятность чего составляет 42,85 %. На остальные параметры гипотеза о влиянии смены не подтверждается. При разработке АСУТП необходимо учитывать это обстоятельство.

Поскольку параметры «декада» и «смена» значительно отличаются друг от друга, то в дальнейшем нужно учитывать влияние всех группировочных признаков. В случае же совпадения параметра можно учитывать влияние только какого-нибудь одного группировочного признака.

Порядок выполнения работы

1. Изучить процедуру проведения однофакторного дисперсионного анализа по данным табл. 1 приложения на основе теоретического материала, представленного в [2].

2. На основе аналитической группировки выбрать из заданного варианта массива данных с наибольшим влиянием атрибутивного признака.

3. Рассчитать для каждого массива данных значение критерия Фишера, опираясь на лекционный материал.

4. Провести дисперсионныйанализ по предложенной методике.

Контрольные вопросы

1. Что представляет собой критерий Фишера?

2. Что такое межгрупповая оценка дисперсии?

3. Каким образом проводится проверка статистических гипотез.

4. В чем сущность процедуры дисперсионного анализа?

5. Можно ли провести однофакторный дисперсионный анализ, не разбив общую совокупность на несколько уровней?

Таблица 5.2

Показатели	Расчетные формулы	Содержание Ме в руде	Выход. конц.	Содержание S в конц.	Содержание Ме в хвост.	Содержание Ме в сульф.
Различия между уровнями		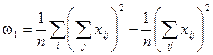0,042	0,107	0,012	0,001	0,50
Различия внутри уровней		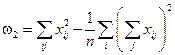0,249	0,495	0,179	0,015	0,67
Сумма	ω = ω1 + ω2	0,291	0,602	0,191	0,015	1,18
Межгрупповая оценка дисперсии	σ12 = ω1 / p – 1	0,021	0,05	0,0062	0,0005	0,20
Внутригрупповая оценка дисперсии	σ22 = ω2 / N – p	0,009	0,02	0,0066	0,0005	0,01
Расчетное значение критерия Фишера	Fрасч	2,281	2,92	0,94	0,8418	10,12
Табличное значение критерия Фишера	Fтабл	2,99	2,99	2,99	2,99	2,90
%		14,45%	17,78%	6,48%	5,87%	42,85%

Лабораторная работа 6