Седьмое уравнение Максвелла

Седьмое уравнение Максвелла представляет собой закон сохранения электрического заряда, который может быть записан в различных формулировках. Чтобы их использовать, рассмотрим подробно все понятия, связанные с законом сохранения электрического заряда.

Закон сохранения электрического заряда был сформулирован Фарадеем в 1834 году. В современной формулировке он читается следующим образом: алгебраическая сумма зарядов всех частиц и всех античастиц в замкнутой системе остается величиной постоянной.Эта формулировка представляет собой физическую сущность седьмого уравнения Максвелла.

Для математической записи этого закона используются следующие известные физические величины:

1. Сила электрического тока или сила тока 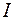: Сила тока – это скалярная физическая величина, численно равная количеству электричества, которое проходит через сечение проводника за единицу времени:

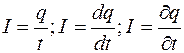(2.46)

Здесь 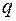- заряд, 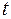- время.

2. Плотность электрического тока или плотность тока 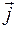:Плотность тока – это векторная физическая величина, численно равна отношению силы тока к площади поперечного сечения проводника, перпендикулярного направлению движения зарядов. Вектор плотности тока направлен по направлению движения положительных зарядов в проводнике:

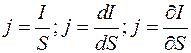(2.47)

Здесь 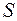- площадь поперечного сечения проводника. Сечение перпендикулярно направлению движения положительных зарядов.

3. Объемная плотность заряда 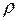: Объемной плотностью заряда называется физическая величина, равная количеству электричества, заключенного в единице объема:

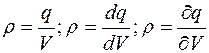(2.48)

Закон сохранения электрического заряда в интегральной форме записывается следующей формулой:

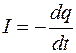(2.49)

Это равенство записано из следующих соображений. Будем считать направление электрического тока положительным, если движение положительного заряда происходит из некоторого объема наружу. Если положительные заряды движутся в противоположном направлении, то направление электрического тока будем считать отрицательным. После этого условия становится понятным знак «минус» в формуле (2.49).

В общем виде формула (2.49) записывается через частные производные, так как заряд может зависеть не только от времени, но и от координат:

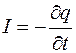(2.50)

Формула (2.50) представляет собой закон сохранения электрического заряда в интегральной форме.

Выразим заряд через объемную плотность заряда:

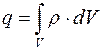(2.51)

Выразим силу тока через плотность тока:

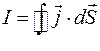(2.52)

Подставляем формулы (2.51) и (2.52) в формулу (2.50):

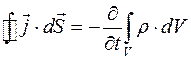(2.53)

Применим к левой стороне формулы (2.53) теорему Гаусса:

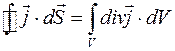(2.54)

Подставляем формулу (2.54) в формулу (2.53) и получаем:

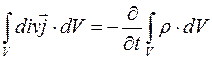(2.55)

Поменяем порядок дифференцирования, и интегрирования в правой части формулы (2.55) и получаем:

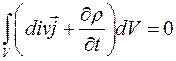(2.56)

Интеграл равен нулю при отличном от нуля объеме интегрирования, если подынтегральное выражение равно нулю:

(2.57)

Формула (2.57) представляет собой закон сохранения заряда в дифференциальной форме.

Таким образом, седьмое уравнение Максвелла имеет вид:

1) в интегральной форме: ;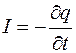

2) в дифференциальной форме: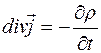

Обе формы записи выражают закон сохранения электрического заряда.