Суммы, произведения и бином Ньютона

Множества

Множество -- неопределяемое понятие. Запись 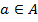означает, что элемент 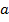принадлежит множеству 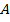. Отношение принадлежности также неопределяемо. Запись 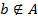значит, что элемент 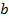не принадлежит множеству 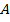. Среди всех множеств есть пустое множество ∅, которое не содержит ни одного элемента. Два множества равны, если и только, если они состоят из одних и тех же элементов (аксиома).

Множество, состоящее из элементов 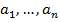, записывается как 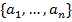. Различают конечные и бесконечные множества. Если множество бесконечно, то очень часто его задают следующим образом:

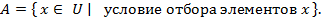
Здесь 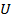-- некоторое универсальное множество, из которого и отбираются элементы. Например, 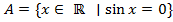-- множество всех действительных чисел, синус которых равен нулю. Это множество совпадает с множеством {0,± π ,± 2π ,± 3π ,… }.

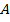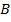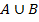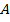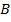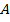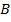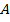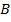Объединением множеств и называется множество , состоящее из всех элементов, принадлежащих либо , либо . Пересечением множеств A и B называется множество A∩B, состоящее из всех элементов, принадлежащих как , так и . Разностью множеств и называется множество 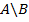, состоящее из всех элементов, принадлежащих 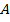, но не принадлежащих .

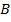Множество 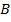называется подмножеством множества 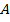, если всякий элемент из B принадлежит также и 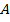. Записывается это отношение так: 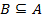или 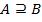. Здесь употреблен символ нестрого включения. Если мы хотим выразить, что 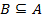и 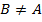, то пишем 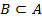(строгое включение). Очередная аксиома теории множеств постулирует, что для любого множества A существует множество всех его подмножеств.

Пара 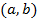это новый математический объект. Пару элементов 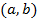можно мыслить как множество из этих двух элементов с дополнительным указанием на то, какой из них первый, какой второй. Считаем, что 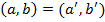в том и только том случае, когда одновременно 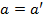и .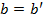

Обозначим через 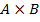-- совокупность всех пар 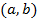, где a пробегает 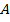, а 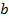пробегает 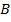. Называется 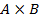декартовым произведением множества A на множество B. В частности, если 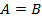, то обозначаем 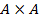как 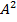и называем декартовым квадратом. Одна из аксиом теории множеств – декартово произведение двух множеств существует, и если эти множества не пусты, то и декартово произведение не пусто.

Логика

Далее мы будем часто пользоваться логической символикой. Пусть 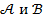-- какие-либо утверждения. Тогда 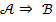значит, что из утверждения 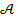следует (вытекает) утверждение 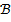. Импликация ложна только в одном случае, когда посылка 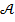истинная, а заключение 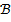ложно. Запись 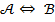значит, что эти утверждения эквивалентны, т.е. справедливость одного влечет справедливость другого. В частности, импликация 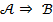эквивалентна утверждению « ».

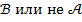Очень часто в математике применяется логическая операция отрицания. Отрицание утверждения 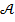обозначаем как 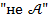. Пусть 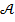и 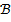-- два утверждения. Тогда

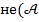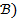и ⇔ не( 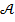) или не ( );

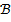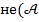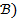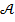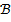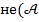
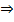
или ⇔ не( ) и 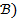не ( );

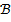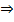⇔ ( не ( ) не( ));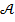

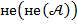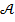⇔ -- «отрицание отрицания»

Пример.Утверждение «не верно, что Васька плут и мошенник» эквивалентно следующему: «или Васька не плут или Васька не мошенник». Утверждение «не верно, что Фигаро здесь или Фигаро там» эквивалентно следующему: «Фигаро и не здесь и не там». Утверждение «не верно, что нет у вас шансов» эквивалентно следующему « у вас есть шанс».

Следует привыкнуть и к так называемым кванторам существования и всеобщности. Запись 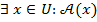значит, что существует элемент 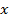из универсального множества 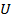(он может быть не единственен), что выполняется условие 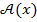, содержащее x как переменную. Например, высказывание 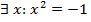звучит так: найдется число 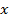, квадрат которого равен -1. Если подразумевать область действительных чисел, то такое высказывание ложно, а для комплексных чисел оно истинно. Итак, знак ∃ заменяет слова "существует, найдется".

Квантор всеобщности ∀ заменяет слова "для любого, всякий, для каждого" и т.п. Например, ∀ x ∈ ℝ ( 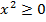) -- верное высказывание, а 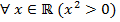-- ложное высказывание.

Доказательство «от противного» основано на том, что для любого утверждения 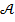верно ровно одно из утверждений: либо 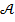, либо его отрицание 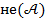. Это можно считать логической аксиомой. Схема доказательства утверждения 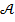«от противного» такова: мы предполагаем, что верно отрицание 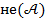и приводим это предположение к противоречию (типа 0=1). Тогда получается, что верно 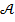. Приведем пример: докажем, что две окружности могут либо не пересекаться, либо касаться в одной точке, либо пересекаться в двух точках, либо совпадать. Предположим противное: две разные окружност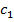и и 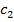имеют боле двух общих точек 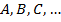. Точки 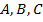не лежат на одной прямой (почему?), следовательно срединные перпендикуляры к отрезкам 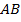и 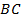пересекаются в одной точке О, равноудаленной от точек 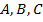. Так как срединный перпендикуляр к хорде проходит через центр окружности, то получаем, что точка О есть центр 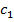и и 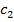. Так как радиусы этих окружностей совпадают с 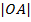, т.е. равны, то получаем 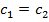-- противоречие с тем, что эти окружности разные. Противоречие показывает, что не могут две разные окружности иметь более двух общих точек. Следовательно, две разные окружности могут иметь 1) две общие точки, 2) одну общую точку (касание), 3) нет общих точек.

Договоримся всюду далее знак ":=" использовать как равенство по определению, т.е. 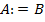означает, что A по определению равно B.

Отображения

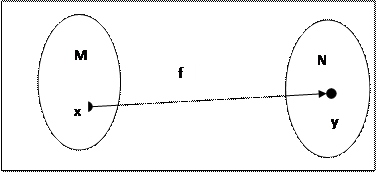
Отображения.Отображением 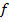множества 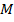в множество 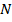(обозначается 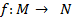) называется правило, в силу которого каждому элементу 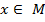ставится в соответствие единственный элемент 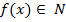. При этом множество 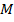называется областью определения (ОДЗ), 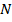-- областью значений, 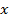-- аргументом, а 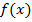-- значением отображения 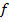на элементе 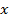или образом элемента 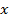при отображении 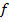. Формально, отображение 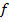задается своим графиком

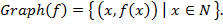
При этом отображение 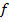отождествляется с тройкой 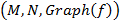. Говорят, что отображение 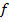взаимно однозначно, если разным значениям аргумента соответствуют разные значения отображения 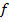. Это эквивалентно следующему условию:

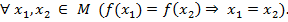
Множество

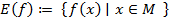
называется областью значений отображения . Очевидно, что 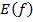есть подмножество множества N. Если 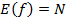, т.е. если для всякого 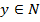найдется хотя бы один аргумент 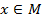(прообраз ) такой, ч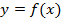то , то 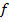назовем отображением множества M на множество N.

Можно задавать отображение таблицей из двух строк, где в первой строке перечислены все возможные аргументы, а во второй – соответствующие им значения. Есл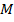и и 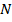числовые множеств, то отображение 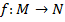называют более точно -- функцией. В этом случае чаще прибегают к аналитическому способу задания функции. Функция задается аналитическим выражением, в которое входят переменная 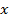, константы и известные и точно определенные операции (арифметические, корни, логарифмы, показательные функции, тригонометрические и т.п.) Естественной ОДЗ аналитического выражения называется совокупность всех чисел, при которых все операции, входящие в аналитическое выражение определены, и получается итоговый результат --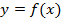

Мы рассмотрели только важнейшие способы задания отображений. Вообще говоря, правило задающие отображение может быть весьма причудливым -- например, отображение Pi из множества ℕ натуральных чисел в множество цифр {0,1,… ,9} такое, что Pi(n) есть цифра, стоящая на n-ом месте в десятичной записи числа π (Pi(1)=1, Pi(2)=4 и т.д.). С другой стороны, правило сопоставляющее натуральному числу n его делитель, не является функцией, ибо отсутствует однозначность образа -- у числа может быть несколько делителей.

Взаимно однозначное отображение и одновременно отображение "на" называется биективным, или биекцией. Если мы сопоставим элементу 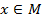сам этот элемент 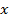, то получим тождественное отображение 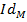которое, конечно, будет биекцией.

Композицией отображени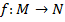й и 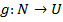называется отображение 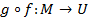такое, что 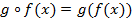для всех 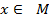. В этом случае функцию 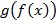называют также подстановкой функции 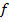в функцию 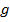. Например, функция 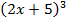получается подстановкой в функцию 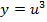функции 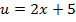. Заметим, что композиция подчиняется закону ассоциативности: если кроме 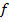и 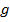имеется еще отображение 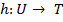, то

.

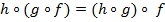Действительно, применяя левую и правую часть этого соотношения к элементу 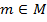, получаем в обоих случаях .

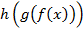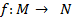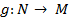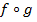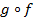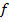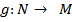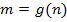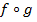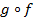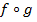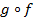Отображение является биекцией в том и только том случае, когда существует отображение , называемое обратным, такое, что и -- тождественные отображения. Обоснуем это. Пусть -- биекция. Определим так, что, если элемент n∈ N произволен, то -- тот единственный элемент, для которого f(m)=n. Легко проверить, что и -- тождественные отображения. Наоборот, пусть и -- тождественные отображения для некоторого 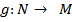. Если 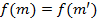, то 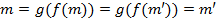и взаимная однозначность следует. Далее, если n∈ N -- произвольный элемент, то 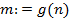тот элемент из N, для которого 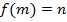. Это доказывает, что 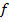есть отображение "на".

Индукция

Метод математической индукции иначе еще называют принципом домино. Представим себе ряд костей домино. Если толкнуть первую кость, то она вызовет падение второй кости, а та в свою очередь третьей и т.д. пока все кости не упадут. Разрушение всей системы основано на двух фактах:

1) первую кость мы толкаем сами,
2) если кость с номером n падает, то она вызывает падение и кости с номером n+1.

Принцип мат. индукции гласит, что даже если в ряду костей домино бесконечное число, то все кости упадут. Трудность состоит в том, чтобы мыслить этот процесс завершенным до конца. Ясно, что никакой реальный эксперимент не может подтвердить такой принцип в точности, но частичное подтверждение этого принципа есть -- результат падения всех костей, даже если их несколько тысяч.

Приведу пример доказательства "по индукции" из теории чисел. Докажем, что для любого натурального n выполняется равенство

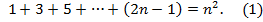
Нам надо обосновать целую серию числовых равенств

(Р1)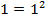
(Р2)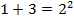
(Р3)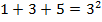
......................
(Рn)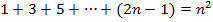

(Р(n+1))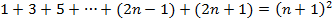
.....................

Что касается первых несколько, то они очевидны и в справедливости их можно убедиться непосредственным вычислением. Но ведь нам надо доказать соотношение (1) сразу для всех n. Поступим так: примем на веру, что утверждение Рn справедливо. Тогда преобразования

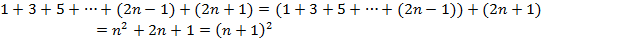
убеждают нас, что и следующее утверждение Р(n+1) также верно. Мы попадем в ситуацию как и с костями домино: первое утверждение проверили, из него вытекает второе, а из него вытекает третье и т.д. до конца. Вот в этом слове "до конца" вся трудность -- конца-то у последовательности натуральных чисел нет. Здесь мы должны прочувствовать и поверить, что если в серии доказываемых равенств первое равенство верно, а из справедливости равенства с номером n вытекает справедливость n+1-го равенства, то все равенства верны. Иными словами мы считаем процесс выведения следующего равенства из предыдущего завершенным.

Наряду с формулой (1) будем далее пользоваться формулами

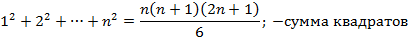
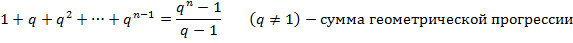
которые можно доказать «по индукции».

Сформулируем теперь отчетливо и строго принцип математической индукции (ПМИ): пусть дан ряд утверждений

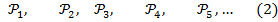
и известно, что

1) 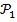-- истинное утверждение (база индукции);

2) если для какого-либо n утверждение 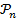верно (индукционное предположение), то и следующее утверждение 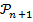также истинно (индукционный переход)

Тогда ПМИ позволяет заключить, что все утверждения 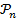верны.

Иногда ПМИ применяется в другой форме: если для ряда утверждений (2) проверена база индукции, а также

2)' из того, что все утверждения 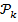справедливы для всех k<n вытекает справедливость n-го утверждения 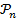, то как и ранее заключаем, что утверждения 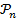верны для всех n.

Приведем пример утверждения из теории делимости натуральных чисел, где при доказательстве используется ПМИ во второй редакции. А именно, докажем основную теорему арифметики: любое натуральное число n>1 разложимо в произведение простых чисел и такое разложение единственно с точностью до перестановки множителей.

Докажем лишь существование разложения. База индукции -- случай n=2. Это наименьшее простое число. Для него теорема верна. Предположим, что мы проверили разложимость в произведение простых всех чисел k меньший n. Если n ни на что не делится, кроме самого себя и единицы, то n -- простое число и n является искомым разложением самого себя. В противном случае, n=k⋅m для натуральных чисел 1<k, m<n. По предположению индукции числа k и m разложимы в произведение простых. Следовательно, и их произведение n также разложимо в произведение простых.

Рекурсия

Пусть нам дана функция одной переменной 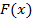и первый член последовательности 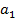. Определим последовательность 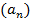так, что

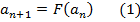
Это фактически есть определение по индукции, где база индукции есть явное задание первого члена последовательности, а индукционный переход есть соотношение (1).

Примеры

1. Определение сложения: 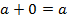и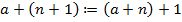

2. Определение умножения: 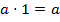и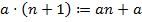

3. Определение степен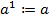и: и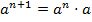

4. Определение факториала: 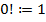и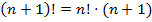

Бывает и более сложная рекурсия, когда задаются явно первые два члена последовательности – 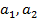, а каждый следующий вычисляется по предыдущим двум по фиксироыванной схеме:

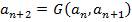
Пример – числа Фибоначчи

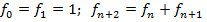
Несколько первых чисел Фибоначчи таковы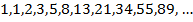

Явная формула для чисел Фибоначчи существует и имеет вид

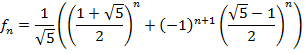
Докажем это. Будем искать числа 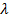такие, что 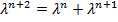для всех натуральных 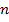. Сокращяя на 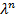получаем квадратное уравнение 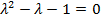(называемое характеристическим), корни которого суть 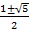. Любая линейная комбинация степеней 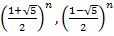, т.е. последовательность вида 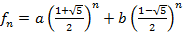также будет удовлетворять рекурентному соотношению 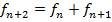. Остается выбрать 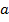и 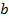так, чтобы удовлетворить начальным условиям :

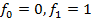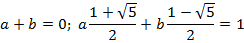
Отсюда 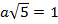и , .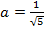

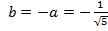Суммы, произведения и бином Ньютона

Этот вспомогательный параграф содержит чрезвычайно часто употребляемые в математике операторы суммирования и произведения, а также формулу бинома Ньютона, обобщающую известные формулы квадрат суммы и куб суммы двух чисел.

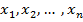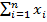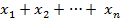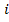Пусть задано конечное семейство чисел . Тогда выражение обозначает их сумму , а называется индексом суммирования, который пробегает от 1 до n. Аналогично, 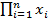обозначает произведение 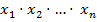семейства чисел 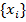. Если мы заменим индекс суммирования на любую другую букву, то результат применения операторов суммирования и произведения не изменится. Строго, сумма 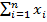определяется рекурсивно по последовательности 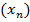как

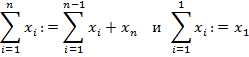
Аналогично

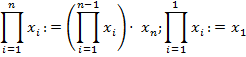
Если все числа 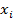из семейства равны одному и тому же числу d, то 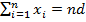и 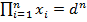. Отметим свойство линейности суммы:

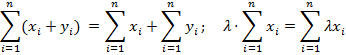
В этом смысле оператор суммирования проще (и чаще употребительней) оператора произведения, свойство линейности для последнего не выполняется.

Факториал натурального числа n есть произведение всех натуральных чисел от 1 до n включительно. Обозначается факториал как n!. Полагаем также по определению 0!=1. Получаем

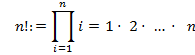
Подсчет 1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720, 7!=5040, 8!=40320, … убеждает нас, что факториал -- очень быстро растущая функция.

Решим теперь такую комбинаторную задачу: сколькими способами можно выбрать k предметов из n предметов. Обозначим это число 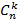(читается: "це из эн по ка"). В некоторых частных случаях ответ прост: 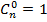, , 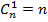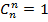. Формула 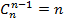получается после некоторого размышления -- выбор n-1 предмета из n предметов равносилен "невыбору" одного предмета из тех же n предметов. Иными словами 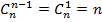. Обобщая это правило на случай k предметов, получим:

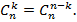
Фиксируем один предмет 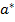среди данных n предметов A. Тогда все выборы k предметов из A, т.е. все подмножества B⊆ A содержащие k предметов разбиваются на два класса -- те, что содержат 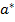и те, что не содержат 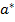. В первом классе 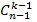подмножеств (остается выбрать k-1 предмет из 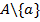), а во втором классе 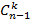подмножеств (все k предметов выбираем из множества 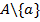). Получаем:

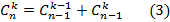
Этой формулой можно пользоваться для всех 1≤ k≤ (n-1) и n≥ 1. Вместе с "граничными условиями" 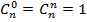это дает способ вычисления всех чисел 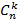. Соотношения (3) также представляют из себя рекуррентные формулы.

Получаем так называемый треугольник Паскаля

1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
..... .. .. .. .. .. .. .. .. .. .. .. .....

В этом треугольнике n-ая строка сверху содержит числа 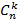при k=0,1,2,… , n. Любое число, кроме самых крайних слева и справа равно сумме чисел стоящих над ним (4=1+3, 6=3+3, и.т.д.) Имеется и прямая, не рекуррентная формула для чисел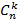

Предложение. Для всех n≥ 1 и всех 0≤ k≤ n имеет место равенство

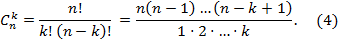
Обозначим пока 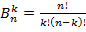. Имеем:

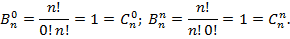
Иными словами, краевые условия совпадают. Докажем, что числа 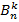удовлетворяют рекуррентному соотношению (3).

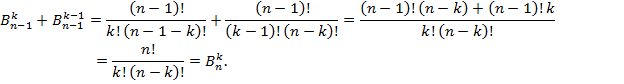
Теперь очень легко индукцией по n доказать, что имеет место равенство 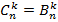для всех допустимых k. Действительно, база индукции, n=1 проверяется прямым подсчетом. Предполагая далее верным равенство 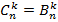при всех 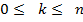докажем равенство 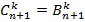для всех 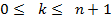. Во-первых, это так 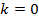для и для 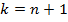в силу совпадения граничных условий. Для остальных 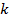воспользуемся рекуррентным соотношением и предположением индукции:

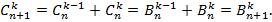
Бином Ньютона. Для любого натурального n имеет место равенство

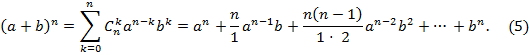
Доказательство. Раскрывая скобки в произведении

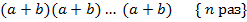
мы видим, что количество слагаемых, у которых степень по 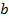равна 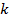, а степень по 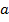равна 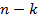совпадает с числом выборов 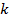предметов из n предметов, т.е. с .

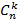Возможен и другой способ доказательства бинома Ньютона -- индукцией по степени n. Тогда следует применить рекуррентные формулы (3). В связи формулой бинома Ньютона числа 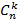называют биномиальными коэффициентами.

Пример

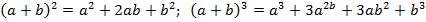
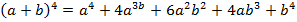
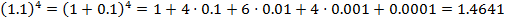
Крупное достижение Ньютона состоит в том, что формулой (5) можно пользоваться и в случае нецелого 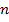. Правда в этом случае справа получается бесконечная сумма:

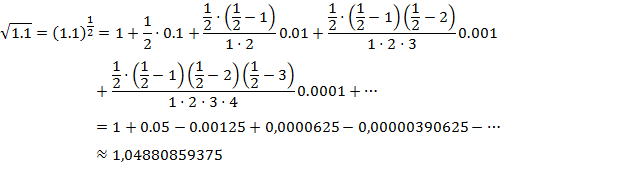
Точное значение 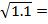1,0488088481701515469914535136799…