Шбұрыштардың екі бұрышы бойынша ұқсастық белгісі

Теорема 2. Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың eкі бұрышына тең болса, ондай үшбұрыштар ұқсас болады.

Д ә л е л д е у. Айталық, ABC және А₁В₁С₁ үшбұрыштарында 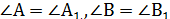болсын. Сонда, ∆ABC ∞ ∆А₁В₁С₁ болатынын дәлелдейміз.

Айталық, 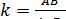болсын. А₁В₁С₁үшбұрышына ұқсастық

коэффициенті k болып келген қандай да бip ұқсас түрлендіруді, мысалы гомотетияны қолданайық (9-сурет). Сонда АВС үшбұрышына тең қандай да бip A₂В₂C₂ үшбұрышы шығады. Шынында да, ұқсас түрлендіру бұрыштарды сақтап қалдыратындықтан, 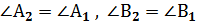болады. Олай болса, АВС және A₂В₂C₂ үшбұрыштарында 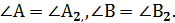Әрі қарай, 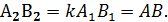Олай болса, ABC және A₂В₂C₂ үшбұрыштары екінші белгі бойынша (қабыр- ғасы мен оған іргелес жатқан бұрыштары бойынша) тең бо­лады.

9-сурет

А₁В₁С₁ және A₂В₂C₂ үшбұрыштары гомотетиялы, ендеше, ұқсас болатындықтан, ал A₂В₂C₂ және ABC үшбұрыштары тең және сондықтан ұқсас болатындықтан А₁В₁С₁ және ABC үш­бұрыштары ұқсас болады. Теорема дәлелденді [27].

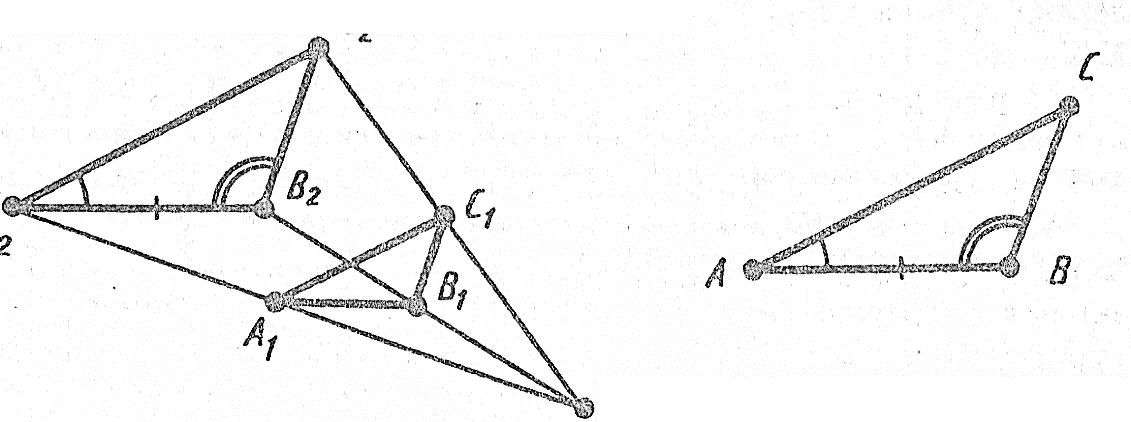
Есеп (2). АВС үшбұрышының АВ қабырғасына параллель жүргізілген түзу оның АС қабырғасын A₁ нүктесінде, ал ВС қабырғасын В₁ нүктесінде қиып өтеді. Сонда ∆АВС ∞ ∆А₁В₁С₁болатынын дәлелдеңдер.

10-сурет

Ш е ш у i (10-сурет). АВС және А₁В₁С₁ үшбұрыштарыныңСтөбесіндегі бұрышы ортақ, алСА₁В₁ және CAB бұрыштары тең, өйткені оларАВменА₁В₁ параллель түзулерін AC түзyi қиып өткенде шығатын сәйкес бұрыштар. Олай болса, eкi бұрышы бойынша∆АВС ∞ ∆А₁В₁С₁болады.

Шбұрыштардың екі қабырғасы және олардың арасындағы бұрышы бойынша ұқсастық белгісі

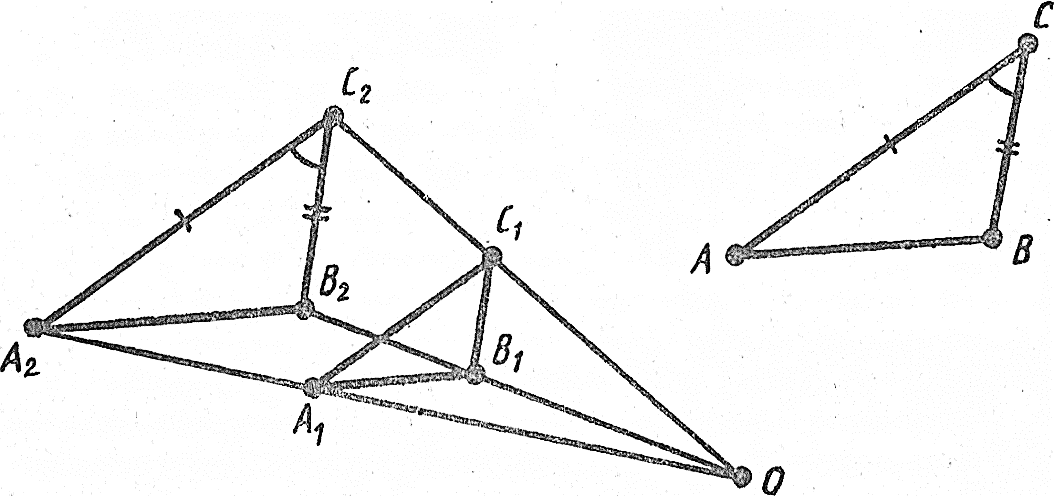
Теорема3. Егер бір үшбұрыштың eкi қабырғасы екінші үшбұрыштың қабырғасына пропорционал болып және осы қабырғалар жасайтын бұрыштар тең болса, ондай үшбұрыштар ұқсас болады [4].

11-сурет

Д ә л е л д е у . (3 теореманың дәлелдеуіне ұқсас дәлелденеді). Айталық, АВС және А₁В₁С₁ үшбұрыштарында 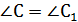және AC = kA₁C₁, BC = kB₁C₁ болсын. Сонда ∆АВС ∞ ∆А₁В₁С₁болатындығын дәлелдейміз.

А₁В₁С₁үшбұрышына коэффициенті kұқсас түрлендіруді, мысалы (гомотетияны, қолданамыз (11-сурет). Сонда ABC үш­бұрышына тең болатын қандай да бip A₂В₂C₂ үшбұрышы шығады. Шынында да, ұқсас түрлендіру бұрыштарды сақтап қалдыратындықтан, 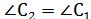болады. Демек, ABC мен A₂В₂C₂ үшбұрыштарының 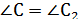болады. Әpi қарай A₂C₂ = kA₁C₁= AC, В₂С₂ ꞊ kВ₁С₁=BC. Олай болса, ABC және A₂В₂C₂ үшбұрыштары бipiншi белгі (eкi қабырғасы және олардың арасындағы бұрышы) бойынша тең болады.

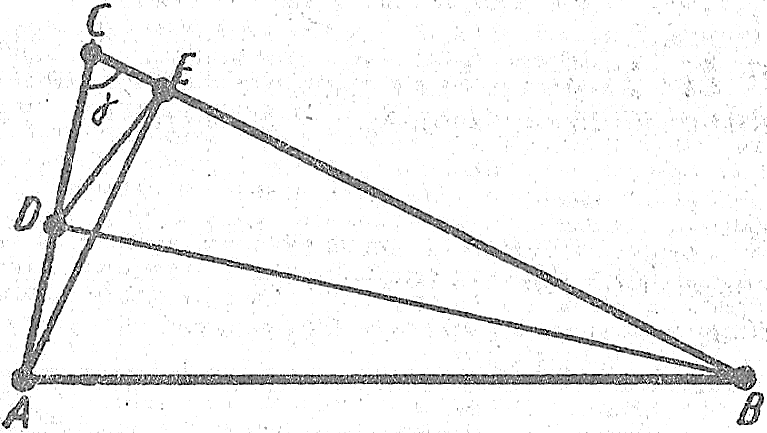
12-сурет

А₁В₁С₁ және A₂В₂C₂ үшбұрыштары гомотетиялы, ендеше ұқсас болатындықтан, ал A₂В₂C₂ және ABС үшбұрыштары тең, сондықтан бұлар да ұқсас болғандықтан, А₁В₁С₁ және АВС үшбұрыштары ұқсас болады. Теорема дәлелденді [4].

Есеп (3). С бұрышы сүйір болып келген ABC үшбұрышының АЕ мен BDбиіктіктері жүргізілген. (12 - сурет). Сонда ∆ABC ∞ ∆EDC болатынын дәлелдеңдер.

Ill е ш у i. ABC мен EDC үшбұрыштарының С төбесіндегі бұрыш екеуіне ортақ. Осы бұрышпен іргелес жатқан қабырғалардың пропорционал болатынын дәлелдейік. Сонда, ЕС꞊AСcosγ, DC꞊ВСcosγ. Яғни үшбұрыштардың Сбұрышына іргелес жатқан қабырғалары пропор­ционал болады. Демек, eкi қабырғасы мен олардың арасындағы бұрышы бойынша ∆ABC ∞ ∆EDC болады.