Формулы Кристофеля – Шварца

Параметрами общей квадратурной формулы являются веса и узлы. Однако, строя формулы трапеций, Симпсона, Эйлера, средних и т.д., мы заранее знали координаты узлов и по ним находили веса. Поэтому мы не полностью использовали возможности общей квадратурной формулы. Только в формуле средних мы в какой-то степени подобрали положение узла из соображений симметрии, что привело к существенному улучшению точности.

В общем случае квадратурная формула содержит всего 2n параметров; столько же содержит полином степени 2n – 1. Значит, параметры (узлы и веса) можно подобрать таким образом, чтобы квадратурная формула

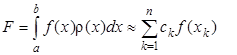(2.19)

была точна для любого многочлена степени не выше 2n – 1. Именно к такому типу формул и относится формула Гаусса – Кристоффеля. Она имеет тот же вид (2.19), но весовая функция с_k определяется по специальной формуле

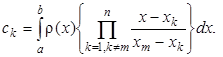(2.20)

Из изложенного следует, что узлами Гаусса – Кристоффеля являются нули соответствующих ортогональных полиномов Р_n(x).. Для наиболее употребительных весовых функций r(х) узлы и веса формул Гаусса – Кристоффеля приведены в следующем пункте.

Рассмотрим некоторые частные случаи.

а) Собственно формуле Гаусса соответствует случай r(х) = 1. Линейным преобразованием аргумента можно перейти к отрезку а = - 1, b = 1. На нём ортогональны с единичным весом многочлены Лежандра. Если обозначить их узлы и соответствующие веса через x_k, g_k, то обратным линейным преобразованием можно получить узлы и веса для произвольного отрезка

x_k = ½ (a + b) + ½ (b – a)x_k,

(2.20,a)

c_k = ½ (b – a)g_k, 1 £ k £ n.

б) Формула Эрмита позволяет интегрировать на отрезке [ - 1, + 1] с весом r(х) = 1/(1 – х²)^1/2. При этих условиях ортогональны многочлены Чебышева первого рода Т_n(x). Соответствующие узлы и веса интегрирования равны

x_k = cos[p(k – ½ )/n], g_k = p/n, 1 £ k £ n. (2.20,б)

в) По формулам Гаусса – Кристоффеля возможно вычисление несобственных интегралов на полупрямой 0 £ х < ¥; если весовая функция равна r(х) = х^aе^-х, то ортогональными будут полиномы Лагерра 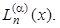То же относится к интегралам на всей прямой - ¥ < х < + ¥ при весе 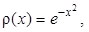только ортогональными будут полиномы Эрмита. Соответствующие примеры приведены в параграфе 2.2.

Ортогональные многочлены

Многочлены P_n(x) называют ортогональными с весом r(х) на отрезке [a, b], если они удовлетворяют соотношениям:

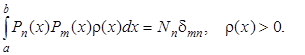(2.21)

По традиции наиболее употребительные полиномы не нормируют на единицу. Все корни ортогональных многочленов вещественные, простые и расположены на интервале (a, b). Между каждой парой соседних корней многочлена P_n(x) расположен один и только один корень многочлена P_n-1(x).

Почти все классические ортогональные полиномы являются частными случаями полиномов Якоби, Лагерра и Эрмита. Они удовлетворяют дифференциальному уравнению

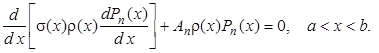(2.22)

Их удобно вычислять либо по обобщённой формуле Родрига

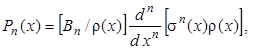(2.23)

либо, зная два первых полинома, при помощи рекуррентных соотношений

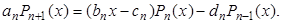(2.24)

Конкретный вид всех встречающихся в этих формулах функций и значения констант приведены в табл. 2.1.

Приведём типичные ортогональные полиномы с небольшими индексами n, их корни 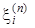и соответствующие им веса 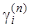формулы Гаусса – Кристоффеля.

Многочлены Лежандра. L₀(x) = 1; L₁(x) = 1; L₂(x) = ½ (3x² – 1); L₃(x) = = ½ (5x³ –3x); L₄(x) = (1/8)(35x⁴ – 30x² + 3); L₅(x) = (1/8)(63x⁵ – 70x³ + 15x).

n = 1; x₁ = 0; g₁ = 2.

n = 2; - x₁ = x₂ = (1/3)^1/2; g₁ = g₂ = 1.

n = 3; - x₁ = x₃ = (3/5)^1/2; x₂ = 0; g₁ = g₃ = 5/9; g₂ = 8/9.

n = 4;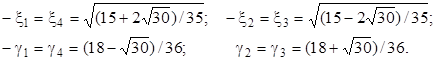

n = 5;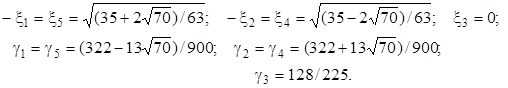

Полиномы Лагерра (a=0).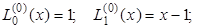

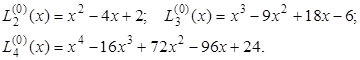
n = 1; x₁ = 1; g₁ = 1.

n = 2; x₁ = 2 – (2)^1/2, x₂ = 2 + (2)^1/2; g₁ = [2 + (2)^1/2]/4; g₂ = [2 – (2)^1/2]/4.

n = 3; x₁ = 0,415775, x₂ = 2,294280, x₃ = 6,289945;

g₁ = 0,711093, g₂ = 0,278518, g₃ = 0,010389.

Многочлены Эрмита. H₀(x) = 1; H₁(x) = 2x; H₂(x) = 4x² – 2; H₃(x) = 8x³ – 12x; H₄(x) = 16x⁴ – 48x² + 12; H₅(x) = 32x⁵ – 160x³ +120x.

n = 1; x₁ = 0; g₁ = (p)^1/2.

n = 2; - x₁ = x₂ = 1/(2)^1/2; g₁ = g₂ = (p)^1/2/2.

n = 3; - x₁ = x₃ = (3/2)^1/2, x₂ = 0; g₁ = g₃ = (p)^1/2/6, g₂ = 2(p)^1/2/3.

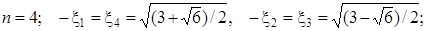
Таблица 2.1. Ортогональные многочлены

Полином	Якоби	Лежандра	Чебышева первого рода	Чебышева второго рода	Лагерра	Эрмита
Обозначение		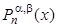Ln(x)	Tn(x)	Un(x)		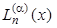Hn(x)
a, b	- 1, + 1	- 1, + 1	- 1, + 1	- 1, + 1	0, + ¥	- ¥, + ¥
r(x)	(1 – x)a(1 + x)b, a, b > - 1		(1 – x2)-1/2	(1 – x2)1/2	xae-x, a > - 1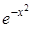
s(x)	1 – x2	1 – x2	1 – x2	1 – x2	x
Nn	2a+b+1G(a + n + 1)G(b + n + 1)/[n!(a + b + 2n + 1)G(a + b + n + 1)]	2/(2n + 1)	p/2 при n ¹ 0, p при n = 0		n! ´ ´G(a + n + 1)	(p)1/22nn!
An	n(n +a + b + 1)	n(n + 1)	n2	n(n + 2)	n	2n
Bn	(- 1)n/(2n×n!)	(- 1)n/(2n´ ´n!)			(- 1)n	(- 1)n
an	2(n + 1)(n + a + b + 1)(2n + a + b)	n + 1
bn	(2n + a + b)(2n + a + b + 1)(2n + a + b + 2)	2n + 1
cn	(b2 - a2)(2n + a + b + 1)				2n + a + 1
dn	2(n + a)(n + b)(2n + a + b + 2)	n			n(n + a)	2n

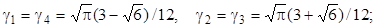
n = 5;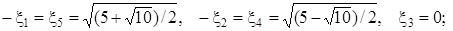

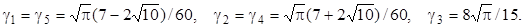
Полиномы Чебышева первого рода. T₀(x) = 1; T₁(x) = x; T₂(x) = 2x² – 1;

T₃(x) = 4x³ – 3x; T₄(x) = 8x⁴ – 8x² + 1; T₅(x) = 16x⁵ – 20x³ + 5x;

T₆(x) = 32x⁶ – 48x⁴ + 18x² – 1; T₇(x) = 64x⁷ – 11x⁵ + 56x³ – 7x.

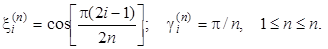
Полиномы Чебышева второго рода. U₀(x) = 1; U₁(x) = 2x; U₂(x) = 4x² – 1;

U₃(x) = 8x³ – 4x; U₄(x) = 16x⁴ – 12x² + 1; U₅(x) = 32x⁵ – 32x³ + 6x.

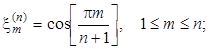
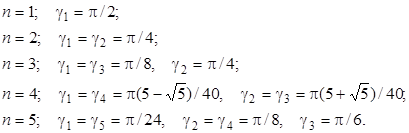
Многочлены на системе точек. Многочлены P_n(x) называют ортонормированными на системе точек x_i с весами r_i (1 £ x £ N), если они удовлетворяют соотношениям

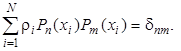
Систему таких многочленов можно построить, используя рекуррентное соотношение

l_nP_n+1(x) = (x – a_n)P_n(x) + b_nP_n-1(x),

где

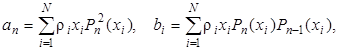
а l_n определяется из условия нормировки. Для начала расчёта по этим формулам нужно положить

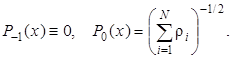
2.2. Нестандартные формулы

Нестандартными называются формулы, предназначенные для вычисления интегралов от функций, имеющих особенности.

Разрывные функции. Пусть функция и её производные кусочно-непрерывны; в точке разрыва подразумевается существование односторонних производных всех требуемых порядков. В этом случае обеспечить требуемую точность интегрирования можно следующим образом.

Разобьём отрезок [a, b] на более мелкие отрезки так, чтобы на этих отрезках функция и некоторое число p её низших производных были непрерывны; на концах этих отрезков в качестве значений функции и производных возьмём соответствующие односторонние пределы.

Представим интеграл в виде суммы интегралов по отрезкам непрерывности. Применим к каждому отрезку квадратурную формулу порядка точности q, q £ p. Если одновременно и одинаково сгущать сетки на всех отрезках непрерывности, то порядок точности ответа будет q, как и для непрерывных достаточно гладких функций. В этом случае методом Рунге можно повысить порядок точности до р.

Пример 2.2. Рассмотрим

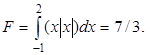
Здесь подынтегральная функция непрерывная и гладкая, но вторая производная имеет разрыв при х = 0. Если для этой функции выделить отрезки непрерывности (- 1 £ х £ 0 и 0 £ х £ 2), то формула Симпсона даёт точный ответ.

Нелинейные формулы. В случае интегрирования быстропеременных функций стараются найти выравнивающие переменные, в которых уже два свободных параметра обеспечивали бы удовлетворительную аппроксимацию. На отрезке [a, b] строят сетку и на каждом интервале сетки функцию заменяют нелинейной интерполяционной функцией, в которой параметры выражены через табличные значения функции. Например, если функция близка к экспоненте, то

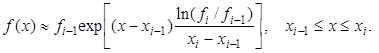
Если на каждом интервале проинтегрировать это выражение вместо исходной функции, то получим обобщённую квадратурную формулу

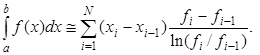(2.25)

Отметим, что второй множитель под знаком суммы является среднелогарифмическим значением функции на элементарном шаге.

Переменный предел интегрирования. Пусть надо вычислить

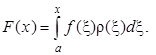
В принципе, при каждом значении х его можно рассматривать как интеграл с постоянными пределами и вычислить одним из приведённых выше способов. Однако если нужно определить интеграл для очень многих значений х, то это невыгодно. Целесообразнее выбрать сетку и численным интегрированием высокой точности составить таблицу значений интеграла на этой сетке F_n = F(x_n). Тогда

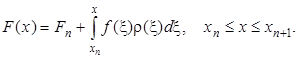
Несобственные интегралы. Для интегралов с бесконечными пределами имеется несколько приёмов вычисления.

Приём 1 – введение такой замены переменных, чтобы превратить пределы интегрирования в конечные. Например, для интеграла

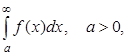
замена x = a/(1 – t) превращает полупрямую [a, ¥) в отрезок [0, 1]. Если после преобразования подынтегральная функция с некоторым числом производных остаётся ограниченной, то можно находить интегралы стандартными численными методами.

Как правило, возможные преобразования "напрашиваются" самим видом подынтегрального выражения. Например, при вычислении интеграла

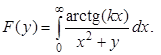
при взгляде на функцию арктангенса сразу приходит на ум соотношение

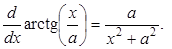
Поэтому приведённый выше интеграл естественным образом заменяется на следующий

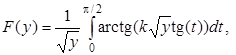
который отыскивается численно элементарным образом.

Приём 2 – обрезание верхнего предела (или обоих пределов). Выберем такое значение b, чтобы

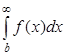
был меньше допустимой ошибки вычислений. Тогда его можно отбросить, а

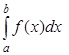
вычислить по квадратурной формуле. Для правильного выбора величины b полезно строить график подынтегральной функции. Например, построение графика подынтегральной функции при вычислении интеграла

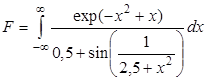
показывает (см. рис. 2.1), что фактически эта функция за пределами – 4 £ х £ 5 равна нулю. Поэтому данный интеграл несобственный только формально. Об этом свидетельствует и почти полное совпадение значений интегралов, вычисленных при разных пределах.

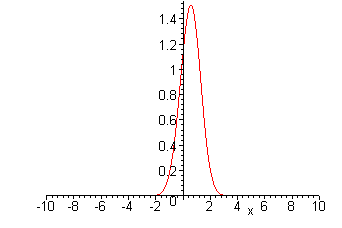
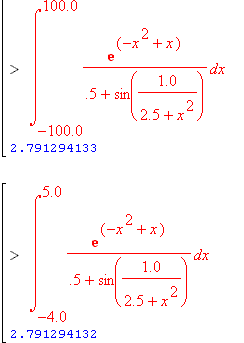
Рис. 2.1. К вычислению несобственного

Интеграла

Приём 3 – использование формул Гаусса – Кристоффеля. Из подынтегральной функции нужно выделить положительный множитель, который можно рассматривать как вес для данных пределов интегрирования. Например, дадим способ вычисления интегральной экспоненты

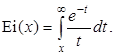
Сдвигая нижний предел (фактически, вводя новую переменную t ' = t – x), приведём этот интеграл к форме

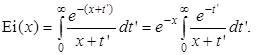
Рассматривая e ^{– t '} как весовую функцию, из анализа данных табл. 2.1 находим, что этому случаю соответствуют полиномы Лагерра при a = 0, т.е. 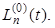Тогда для искомого интеграла получаем

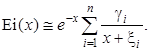(2.26)

Это выражение можно использовать как аппроксимирующую формулу. Например, одному, двум и трём узлам интегрирования соответствуют

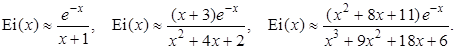
Если первая из этих формул пригодна лишь при больших аргументах, то вторая даёт удовлетворительную точность ~ 5 % уже при х =1, а при больших аргументах точность ещё лучше. Третья формула обеспечивает погрешность ~ 5 % уже при х ³ 0,5, а при х > 1 ошибка вычисления интеграла не превышает 1 %.

Если пределы интегрирования конечны, функция f(x) может иметь особые точки в каких-то точках отрезка [a, b] (т.е. точки, в которых она принимает бесконечные значения). Доля вычисления таких интегралов также имеются специальные приёмы.

Приём 1 – аддитивное выделение особенности. Постараемся разбить подынтегральную функцию на сумму f(x) = j(x) + y(x), где j(x) – ограниченная функция, а y(x) интегрируется аналитическими методами. Тогда 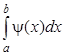вычисляем точно, а 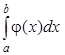находим обычными численными методами. Заметим, что обычно разбиение на сумму делается выделением особенности в наиболее простом виде. Например, если 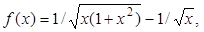то полученная функция будет ограничена, что и требуется.

Приём 2 –мультипликативное выделение особенности. Представим подынтегральную функцию в виде f(x) = j(x)r(x), где j(x) ограничена, а r(x) положительна и интегрируема на отрезке. Тогда можно рассматривать r(x) как весовую функцию и применить квадратурные формулы Гаусса – Кристоффеля. Если на обоих концах отрезка функция имеет особенности степенного вида, то узлами интегрирования будут нули многочленов Якоби. Например,

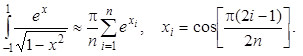(2.27)

Здесь использовались полиномы Чебышева первого рода (см. табл. 2.1).

Приём 3 – построение нестандартных квадратурных формул, явно учитывающих характер особенности. Так, для приведённого выше интеграла (2.27) на отдельном интервале сетки (x_i-1, x_i) можно аппроксимировать подынтегральную функцию выражением exp(x_i-1/2 )/(1 – x²)^1/2, поскольку числитель – медленно изменяющаяся функция и основная особенность связана со знаменателем. Эта аппроксимация легко интегрируется и приводит к квадратурной формуле

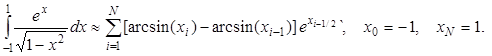(2.28)

Пример 2.3. Перед выполнением численного интегрирования всегда необходимо тщательно анализировать подынтегральную функцию.

Учитывая, что

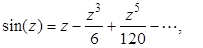
перепишем заданный интеграл в виде

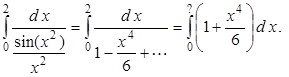
По условию требуется, чтобы погрешность вычисления интеграла не превышала 10 ^-4, следовательно, верхний предел интегрирования, допустимый при указанной аппроксимации определяется из условия

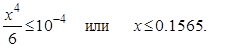
На этом интервале интеграл легко вычисляется

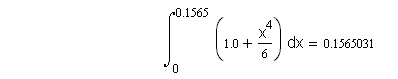
Во второй особой точке в окрестности x² = p или x = p^1/2 sin(x²) » 0. Отметим также, что при x² > p подынтегральная функция изменяет знак. Здесь можно поступить двумя способами. Во-первых, можно просто исключить ближайшую окрестность точки x = p^1/2 из области интегрирования, так как интегралы слева и справа от этой точки компенсируют друг друга. Тогда

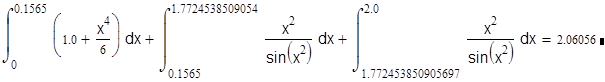
Во-вторых, можно подробно исследовать окрестность точки x = p^1/2. Используя тригонометрические соотношения sin(x²) = sin(p - x²) = -sin(x² - p) и разложение функций в ряды, получим

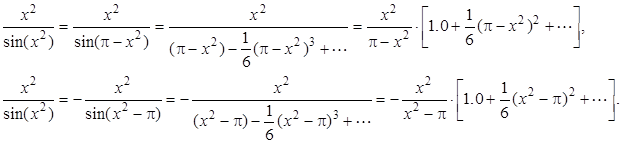В соответствии с требуемой точностью должно быть

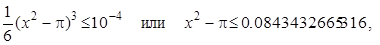
т.е. окрестность точки x = p^1/2 составляет 1.748499467£ x £ 1.796089062. Следовательно, имеем

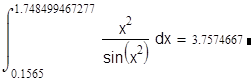
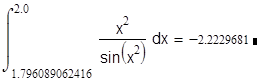
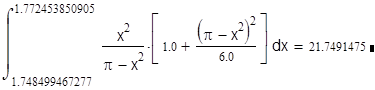
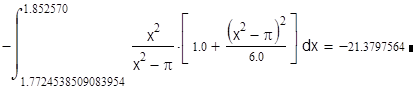
и

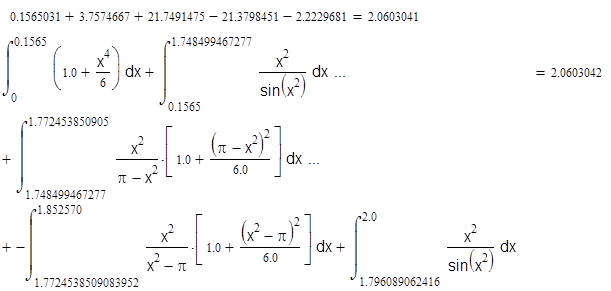
Задание № 4

Вычислить таблицу функции f(y) для ряда равноотстоящих (с шагом h) значений аргумента y, принадлежащих отрезку [a, b].

Точность, с которой требуется получить результат, указана для каждой функции.

Отчёт по заданию должен содержать: 1) обоснование избранного способа вычисления интеграла, 2) вычисления, 3) ответ [таблица функции f(y)], 4) контроль полученной таблицы с помощью разделённых разностей или путём вычисления интеграла с использованием упомянутых выше математических пакетов.

Вариант А

Вариант	Интеграл	k	a	b	h	Точность
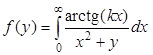		1,0	0,5	1,0	0,05	10-5
	- " -	1,2	0,5	1,0	0,05	10-5
	- " -	1,4	0,5	1,0	0,05	10-5
	- " -	1,6	0,5	1,0	0,05	10-5
	- " -	1,0	1,0	1,5	0,05	10-5
	- " -	1,2	1,0	1,5	0,05	10-5
	- " -	1,4	1,0	1,5	0,05	10-5
	- " -	1,6	1,0	1,5	0,05	10-5
	- " -	1,0	1,5	2,0	0,05	10-5
	- " -	1,2	1,5	2,0	0,05	10-5
	- " -	1,4	1,5	2,0	0,05	10-5
	- " -	1,6	1,5	2,0	0,05	10-5
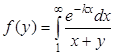		0,8			0.1	10-6
	-"-	0,9			0.1	10-6
	-"-	1,0			0.1	10-6
	-"-	1,1			0.1	10-6
	-"-	0,8			0.1	10-6
	-"-	0,9			0.1	10-6
	-"-	1,0			0.1	10-6
	-"-	1,1			0.1	10-6
	-"-	0,8			0.1	10-6
	-"-	0,9			0.1	10-6
	-"-	1,0			0.1	10-6
	-"-	1,1			0.1	10-6

Вариант Б

Вариант	Интеграл	k	a	b	h	Точность
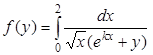		0,8			0,1	10-6
	-"-	0,85			0,1	10-6
	-"-	0,9			0,1	10-6
	-"-	0,95			0,1	10-6
	-"-	0,8			0,1	10-6
	-"-	0,85			0,1	10-6
	-"-	0,9			0,1	10-6
	-"-	0,95			0,1	10-6
	-"-	0,8			0,1	10-6
	-"-	0,85			0,1	10-6
	-"-	0,9			0,1	10-6
	-"-	0,95			0,1	10-6
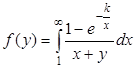		0,6	1,0	1,3	0,03	10-6
	-"-	0,7	1,0	1,3	0,03	10-6
	-"-	0,8	1,0	1,3	0,03	10-6
	-"-	0,8	1,0	1,3	0,03	10-6
	-"-	0,6	1,3	1,6	0,03	10-6
	-"-	0,7	1,3	1,6	0,03	10-6
	-"-	0,8	1,3	1,6	0,03	10-6
	-"-	0,8	1,3	1,6	0,03	10-6
	-"-	0,6	1,6	1,9	0,03	10-6
	-"-	0,7	1,6	1,9	0,03	10-6
	-"-	0,8	1,6	1,9	0,03	10-6
	-"-	0,8	1,6	1,9	0,03	10-6

Вариант В

Вариант	Интеграл	k	a	b	h	Точность
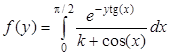		0,4	2,5		0,05	10-6
	-"-	0,45	2,5		0,05	10-6
	-"-	0,5	2,5		0,05	10-6
	-"-	0,55	2,5		0,05	10-6
	-"-	0,4	3,0	3,5	0,05	10-6
	-"-	0,45	3,0	3,5	0,05	10-6
	-"-	0,5	3,0	3,5	0,05	10-6
	-"-	0,55	3,0	3,5	0,05	10-6
	-"-	0,4	3,5	4,0	0,05	10-6
	-"-	0,45	3,5	4,0	0,05	10-6
	-"-	0,5	3,5	4,0	0,05	10-6
	-"-	0,55	3,5	4,0	0,05	10-6
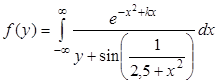		0,7	0,1	0,4	0,03	10-5
	-"-	0,9	0,1	0,4	0,03	10-5
	-"-	1,1	0,1	0,4	0,03	10-5
	-"-	1,3	0,1	0,4	0,03	10-5
	-"-	0,7	0,4	0,7	0,03	10-5
	-"-	0,9	0,4	0,7	0,03	10-5
	-"-	1,1	0,4	0,7	0,03	10-5
	-"-	1,3	0,4	0,7	0,03	10-5
	-"-	0,7	0,7	1,0	0,03	10-5
	-"-	0,9	0,7	1,0	0,03	10-5
	-"-	1,1	0,7	1,0	0,03	10-5
	-"-	1,3	0,7	1,0	0,03	10-5

Вариант Г

Вариант	Интеграл	k	a	b	h	Точность
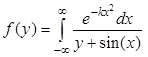		1,1	4,2	4,4	0,02	10-6
	-"-	1,2	4,2	4,4	0,02	10-6
	-"-	1,3	4,2	4,4	0,02	10-6
	-"-	1,4	4,2	4,4	0,02	10-6
	-"-	1,1	4,4	4,6	0,02	10-6
	-"-	1,2	4,4	4,6	0,02	10-6
	-"-	1,3	4,4	4,6	0,02	10-6
	-"-	1,4	4,4	4,6	0,02	10-6
	-"-	1,1	4,6	4,8	0,02	10-6
	-"-	1,2	4,6	4,8	0,02	10-6
	-"-	1,3	4,6	4,8	0,02	10-6
	-"-	1,4	4,6	4,8	0,02	10-6
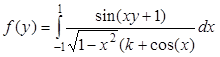		0,2	2,6	2,8	0,02	10-6
	-"-	0,25	2,6	2,8	0,02	10-6
	-"-	0,3	2,6	2,8	0,02	10-6
	-"-	0,35	2,6	2,8	0,02	10-6
	-"-	0,2	2,8	3,0	0,02	10-6
	-"-	0,25	2,8	3,0	0,02	10-6
	-"-	0,3	2,8	3,0	0,02	10-6
	-"-	0,35	2,8	3,0	0,02	10-6
	-"-	0,2	3,0	3,2	0,02	10-6
	-"-	0,25	3,0	3,2	0,02	10-6
	-"-	0,3	3,0	3,2	0,02	10-6
	-"-	0,35	3,0	3,2	0,02	10-6

Пример 2.4. Вычислить интеграл

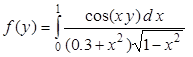
с четырьмя верными знаками после запятой для значений y Î [2.6, 3] с шагом h = 0.04.

Ввиду чётности подынтегральной функции интеграл приводится к виду

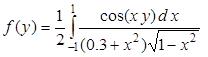
и вычисляется по квадратурной формуле наивысшей алгебраической степени точности с весом (1 – x)^-1/2

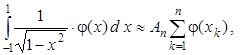
где 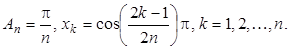Если n чётное, то, используя чётность подынтегральной функции, можно записать

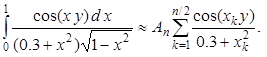
Для того чтобы выбрать число узлов в квадратурной формуле, вычислим f(3) при n = 10, 12 и 14 (следует ожидать, что значение параметра y =3 является самым плохим). Вычисления ведём с одним запасным знаком и заносим в таблицу (см. следующую стр.). Значения интеграла при соответствующем числе узлов получается как сумма произведений чисел, стоящих в четвёртом столбце [cos(3x_k)] на числа, стоящие в последнем столбце.

Поскольку значения интеграла при n = 12 и n = 14 совпали с требуемой точностью, все остальные значения f(y) вычисляем с 12 узлами. При этом для всех следующих интегралов достаточно вычислить лишь x_ky и cos(x_ky). Значения 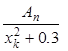уже вычислены.

n	k	xk	cos(3xk)	xk2	xk2 + 0.3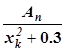
		0.98769	- 0.98410	0.97553	1.27553	0.24630
	0.89100	- 0.89220	0.79388	1.09388	0.28720
	0.70711	- 0.52314	0.50000	0.80000	0.39270
	0.45399	0.20731	0.20611	0.50611	0.62073
	0.15643	0.89189	0.02447	0.32447	0.96822
	f10(3) = 0.28818
		0.99144	- 0.98604	0.98295	1.28295	0.20406
	0.92388	- 0.93234	0.85355	1.15355	0.22695
	0.79336	- 0.72380	0.62942	0.92942	0.28168
	0.60876	- 0.25271	0.37059	0.67059	0.39040
	0.38268	0.41027	0.14644	0.44644	0.58641
	0.13052	0.92432	0.01704	0.31704	0.82576
	f12(3) = 0.28851
		0.99371	- 0.98715	0.98746	1.28746	0.17430
	0.94388	- 0.95235	0.89091	1.19091	0.18843
	0.84672	- 0.82453	0.71693	1.01693	0.22066
	0.70711	- 0.52314	0.50000	0.80000	0.28050
	0.53203	- 0.02529	0.28306	0.58306	0.38486
	0.33028	0.54798	0.10908	0.40908	0.54854
	0.11196	0.94412	0.01254	0.31254	0.71798
	f14(3) = 0.28854

Приведём в качестве примера два результата вычислений

y	xky	cos(xky)	y	xky	cos(xky)
2.60	2.57774	- 0.84520	2.64	2.61740	- 0.86573
2.40209	- 0.73880	2.43904	- 0.76320
2.06274	- 0.47234	2.09447	- 0.50006
1.58278	- 0.01198	1.60713	- 0.03633
0.99497	0.54453	1.01028	0.53162
0.33935	0.94297	0.34457	0.94122
f(2.6) = 0.62012	f(2.64) = 0.58406

И т.д. Полученные результаты полезно проверить таблицей разделённых разностей.

yi	f(yi)	f(yi,yi+1)	f(yi,yi+1,yi+2)
2.6	0.6201
		-0.9
2.64	0.5841		0.15625
		-0.8875
2.68	0.5486		0.1875
		-0.8725
2.72	0.5137		0.21875
		-0.855
2.76	0.4795		0.1875
		-0.84
2.8	0.4459		0.1875
		-0.825
2.84	0.4129		0.25
		-0.805
2.88	0.3807		0.21875
		-0.7875
2.92	0.3492		0.25
		-0.7675
2.96	0.3185		0.21875
		-0.75
	0.2885

3. СИСТЕМЫ УРАВНЕНИЙ

Решение систем алгебраических уравнений является сущностью инженерной работы в области анализа закономерностей протекания технологических процессов, установления наиболее рационального с точки зрения экономики распределения ресурсов, проектирования систем автоматического управления и т.д. Это объясняется тем, что в силу существенной нелинейности реальных процессов их математические модели характеризуются существенной нелинейностью и не могут быть решены аналитически. Поэтому, как правило, их решают численно на ЭВМ, а для этого необходимо свести (аппроксимировать) дифференциальные уравнения данных моделей к системе алгебраических соотношений (получить численную модель или дискретный аналог математической модели).

Как и исходные математические модели процессов или агрегатов, алгебраические уравнения, входящие в численную модель, могут быть линейными и нелинейными. Процедуры решения систем уравнений в этих случаях существенно различаются, хотя и имеют также много общего.

Линейные системы

В инженерных приложениях встречаются преимущественно нелинейные задачи и, следовательно, решать приходится системы нелинейных уравнений. Однако все методы решения систем нелинейных уравнений базируются на том или ином методе линеаризации исходной системы, поэтому теория линейных систем является основой и для решения нелинейных систем.

Задачи линейной алгебры

Выделяют четыре основных задачи линейной алгебры:

· решение системы линейных уравнений Ax= b, где A – квадратичная матрица иx, b – векторы;

· отыскание (вычисление) обратной матрицы А^-1;

· вычисление определителя det|A|;

· определение собственных значений и собственных векторов матрицы.

Прежде чем решать любую систему уравнений, необходимо выяснить два вопроса: имеет ли вообще данная система решение и, если имеет, то какова точность этого решения?

Ответы на оба эти вопроса связаны с понятием обусловленности матрицы. Чтобы выяснить смысл этого понятия, рассмотрим следующие положения, не вникая в математическую сторону вопроса.

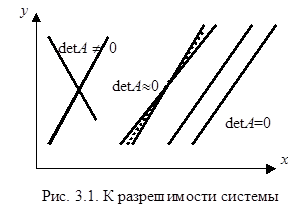Во-первых, как показывает геометрическая интерпретация процедуры решения двух уравнений (см. рис. 3.1), не всякая система имеет решение. Каждому уравнению соответствует прямая в плоскости х, у, а точка пересечения этих прямых и есть решение системы (для n уравнений решение есть точка пересечения всех n гиперплоскостей в n-мерном пространстве). Если detA = 0, то наклоны прямых равны, и они либо параллельны, либо совпадают. В противном случае прямые имеют единственную точку пересечения.

В реальных промышленных условиях данные известны с некоторой не вполне определённой точностью (иногда они попросту лживы). Поэтому весьма важно выяснить надёжность решения при определённой недостоверности исходных данных. Именно эту задачу решает выяснение обусловленности матрицы.

Пусть detA » 0. Запишем формальное решение системы Ax = b в виде x = A^-1b. Варьируя последнее равенство и определяя вариацию обратной матрицы из соотношения dE = d(AA^-1) = AdA^-1 + dAA^-1=0, получим

dx = A^-1(db - dA×x).

Формально устойчивость есть, так как при detA ¹ 0 обратная матрица существует. Но если матрица А^-1 имеет большие элементы, то можно указать такой вид погрешности исходных данных (dbили dА), который сильно изменит решение. В этом случае систему называют плохо обусловленной. Очевидно, у плохо обусловленной системы detA » 0 (рис. 3.1), однако заметим, что этот признак плохой обусловленности является необходимым, но не достаточным.

В теоретических исследованиях обусловленность часто характеризуют числом c = ||A||×||A^-1||. Это число зависит от того, какая норма матрицы выбрана, но при любой норме c ³ 1. Чем больше это число, тем хуже обусловленность матрицы: обычно c ~ 10³ – 10⁴ уже означает плохую обусловленность.

Недостаток данного числа обусловленности состоит в том, что предварительно необходимо выполнить операцию обращения матрицы, а при плохо обусловленной матрице это сделать нелегко. Поэтому в настоящее время, учитывая вспомогательный характер операции определения числа обусловленности матрицы, для этой цели рекомендуется использовать распространённые математические пакеты.

В рамках пакета MATLAB обусловленность матрицы устанавливается с помощью следующих функций:

k = cond(A) k = condest(A) k = cond(A, p) [k, v] = condest(A)

Функция k = cond(A) возвращает число обусловленности матрицы А по отношению к операции обращения, равное отношению максимального сингулярного числа к минимальному: k = s_max/s_min.

Функция k = cond(A, p) возвращает число обусловленность матрицы А относительно р-нормы k º c = norm(A, p)×norm(inv(A), p), где p = 1, 2, inf, 'fro'.

Функция k = condest(A) возвращает оценку нижней границы числа обусловленности матрицы по 1-норме.

Функция [k, v] = condest(A) возвращает помимо оценки нижней границы числа обусловленности также и вектор, такой, что справедливо соотношение norm(Av, 1) = norm(A, 1)×norm(v, 1)/k. Таким образом, вектор v может служить аппроксимацией нуль-вектора матрицы А, если k велико.

Более наглядным является результат выполнения функции k_1 = = rcond(A), которая возвращает величину, обратную значению числа обусловленности матрицы А по 1-норме. Если матрица А хорошо обусловлена, то значение k_1 близко к единице; если матрица А плохо обусловлена, то значение k_1 близко к нулю.

Пример 3.1. Выясним обусловленность матриц коэффициентов следующих двух систем уравнений:

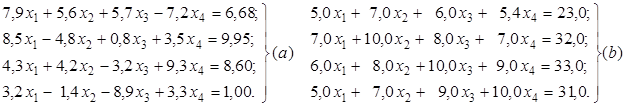Сформируем матрицы систем (а) и (b):

>> A = [7.9 5.6 5.7 -7.2; 8.5 -4.8 0.8 3.5; 4.3 4.2 -3.2 9.3; 3.2 -1.4 -8.9 3.3]

A =

7.900000 5.600000 5.700000 -7.200000

8.500000 - 4.800000 0.800000 3.500000

4.300000 4.200000 - 3.200000 9.300000

3.200000 - 1.400000 - 8.900000 3.300000

>> B = [5 7 6 5; 7 10 8 7; 6 8 10 9; 5 7 9 10]

B =

5 7 6 5

7 10 8 7

6 8 10 9

5 7 9 10

Теперь вычислим параметры матриц:

>> k = cond(A) k_1 = rcond(A) k1 = condest(A)

k = k_1 = k1 =

2.547891 0.417639 5.118441

>> k2 = cond(B) k2_1 = rcond(B) k20 = condest(B)

k2 = k2_1 = k20 =

2.9841e³ 3.0882e^{- 4} 4.4480e³

Таким образом, можно сделать вывод, что матрица А хорошо обусловлена, а матрица В – плохо обусловлена.

В рамках пакета Mathcad вычисляется четыре числа обусловленности:

cond1(A)– возвращает число обусловленности матрицы, вычисленное в 1-норме;

cond2(A)– возвращает число обусловленности матрицы, вычисленное в норме L₂;

conde(A)– возвращает число обусловленности матрицы, вычисленное в норме евклидова пространства;

condi(A)– возвращает число обусловленности матрицы, основанное на равномерной норме.

В данном случае формирование матрицы осуществляется предельно просто – необходимо использовать опции Insert/Matrix, указать число строк и столбцов и ввести соответствующие элементы

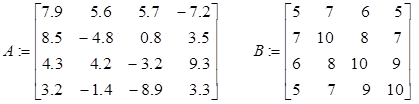
Далее вычисляем характеристики матриц:

cond1(A) = 5.118441, cond2(A) = 2.547891, conde(A) = 5.190408, condi(A) = 5.660286

cond1(B) = 4488, cond2(B) = 2984.092702, conde(B) = 3009,578708, condi(B) = 4488

Сопоставляя результаты оценки обусловленности матриц в MATLAB и Mathcad, можно видеть эквивалентность команд (функций) cond(A)и cond2(A), condest(A)и cond1(A).

В рамках пакета Maple V любого релиза имеется лишь одна функция определения числа обусловленности матрицы cond(A, namenorm), но она охватывает все четыре команды Mathcad, так как опция namenorm может иметь четыре значения: 1, 2, infinity и 'frobenius'. При этом справедлива следующая эквивалентность:

cond1(A) ® cond(A, 1); cond2(A) ® cond(A, 2); condi(A) ® cond(A, infinity);

conde(A) ® cond(A, 'frobenius')

Формирование матриц в Maple осуществляется командой

> A := matrix(4, 4, [[7.9,5.6,5.7,-7.2],[8.5,-4.8,0.8,3.5],[4.3,4.2,-3.2,9.3],[3.2,-1.4,8.9,

3.3]]);

При этом в версиях пакета до Maple V Release 5 на рабочей странице выпечатывается матрица

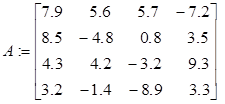
В версии пакета Maple 6 матрица не выпечатывается, а повторяется команда ввода.

Методы решения линейных систем уравнений делятся на прямые и итерационные. Прямые методы дают решение за конечное число действий, просты и наиболее универсальны. Для систем небольшого порядка n £ 200 применяются практически только прямые методы. Итерационные методы выгодны для систем специального вида со слабо заполненной (разрежённой) матрицей очень большого порядка n » 10³ ¸ 10⁵. Сравнительно недавно для решения плохо обусловленных систем стали применять методы регуляризации.

Метод исключения Гаусса

Пусть имеется система уравнений

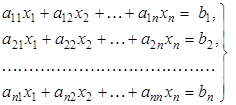(3.1)

или в индексных обозначениях

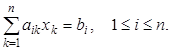(3.1,а)

Метод Гаусса для произвольной системы основан на приведении матрицы системы к треугольному виду. Вычтем из второго уравнения системы (3.1) первое, умноженное на такое число, чтобы уничтожился коэффициент при х₁. Затем таким же образом вычтем первое уравнение из третьего, четвёртого и т.д. Тогда исключатся все коэффициенты первого столбца, лежащие ниже главной диагонали.

Затем при помощи нового второго уравнения исключим из третьего, четвёртого и т.д. уравнений коэффициенты второго столбца. Последовательно продолжая этот процесс, исключим из матрицы все коэффициенты, лежащие ниже главной диагонали.

Запишем общие формулы процесса. Пусть проведено исключение коэффициентов из (k – 1)-го столбца. Тогда остались такие уравнения с ненулевыми элементами ниже главной диагонали:

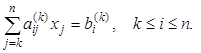(3.2)

Умножим k-тую строку на число

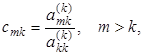(3.3)

и вычтем из m-ной строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам

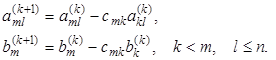(3.4)

Производя вычисления по этим формулам при всех указанных индексах, исключим элементы k-того столбца. Будем называть такое исключение циклом процесса. Выполнение всех циклов называется прямым ходом исключения.

Запишем треугольную систему, получающуюся после выполнения прямого хода. При приведении системы к треугольному виду освободятся клетки в нижней половине матрицы системы (3.1). На освободившиеся места матрицы поставим множители c_mk; их следует запомнить, так как они потребуются при обращении матрицы или уточнении решения. Получим

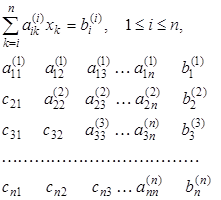(3.5)

Треугольная система (3.5) легко решается обратным ходом исключения. Из последнего уравнения системы сразу находим: 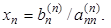Затем последовательно снизу вверх находим все остальные неизвестные по формуле

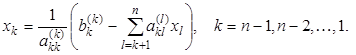(3.6)

Замечания. Исключение по формулам (3.2) – (3.4) нельзя проводить, если в ходе расчёта оказался нулевой элемент 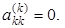Но в первом столбце промежуточной системы (3.2) все элементы не могут быть нулями: это означало бы, что detA = 0. Перестановкой строк можно переместить ненулевой элемент на главную диагональ и продолжить расчёт.

Если элемент на главной диагонали 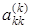мал, то эта строка умножается на большое число c_mk, что приводит к большим ошибкам округления при вычислениях. Чтобы избежать этого, каждый цикл исключения всегда начинают с перестановки строк. Среди элементов столбца 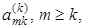находят главный, т.е. наибольший по модулю в k-том столбце, и перестановкой строк переводят его на главную диагональ, после чего производят исключения. Такая процедура называется методом Гаусса с выбором главного элемента.

Для контроля процесса полезно найти невязки: