А. Вертикальные асимптоты.
Напомним, что прямая х=а является вертикальной асимптотой графика функции у=у(х), если хотя бы один из пределов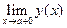 
или 
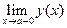равен бесконечности. Прямая х=а может быть (а может и не быть) вертикальной асимптотой только, если а - точка разрыва функции.
В исследуемой функции имеются две точки разрыва. При стремлении к этим точкам знаменатель дроби стремится к нулю, а числитель к ненулевой конечной величине. Следовательно, выражение будет стремиться к бесконечности. Знак бесконечности можно определить из таблицы интервалов знакопостоянства функции. Например, в окрестности точки х=-1 (x<-1) функция положительна. Следовательно
= 
.
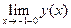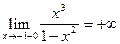Аналогично:
= 
;
= 
;
= 
.
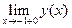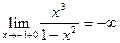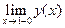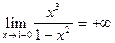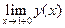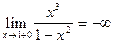Б. Наклонные асимптоты. (Горизонтальные асимптоты мы также относим к наклонным).
Напомним, что прямая y=kx+b является наклонной асимптотой графика функции y=y(x) при x®+¥, если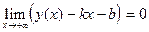 
.
Достаточные условия существования асимптот и формулы для нахождения параметров k и b имеют вид.
; 
.
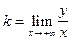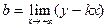Если хотя бы один из этих пределов не существует или равен бесконечности, то функция не имеет асимптот при x®+¥. Аналогично определяется асимптота при x®-¥.
В исследуемой задаче асимптоты при x®-¥ и при x ®+¥ одинаковы. Поэтому мы будем рассматривать предел при x ®¥.
.
.
 |
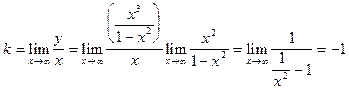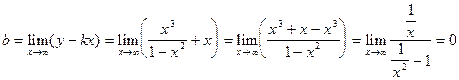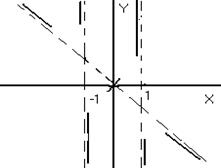Уравнение наклонной асимптоты имеет вид y=-x.
С этого момента на черновике можно начинать строить схему графика. Нанесем точки пересечения с осями координат, асимптоты и поведение функций около асимптот.
Интервалы возрастания, убывания функции. Точки экстремума.
Напомним достаточные условия возрастания (убывания) на отрезке.
Если производная функции положительна (отрицательна) во всех точках отрезка, то функция возрастает (убывает) на этом отрезке.
Необходимые и достаточные условия экстремума были сформулированы ранее.
Найдем производную функции.
.
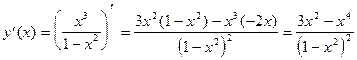А. Интервалы возрастания, убывания функции.
Определим интервалы знакопостоянства производной, они же интервалы возрастания и убывания функции.
Интервалы знакопостоянства производной определяются по той же схеме, что и ранее определялись интервалы знакопостоянства функции.
Производная имеет точки разрыва при х=-1, х=1.
Выясним, где производная равна нулю: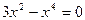 
; 
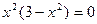; х=0, 
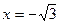, x=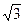 
. 
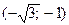
Точки х=-1, х=1, х=0, ,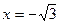 
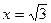разбивают числовую ось на 6 интервалов. Как и ранее определяем знак производной на каждом интервале. По знаку производной делаем вывод о характере поведения функции на интервале (возрастание или убывание). Результаты удобно свести в таблицу. В таблице
знак указывает на возрастание функции, знак на убывание.
| x | 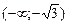 | 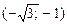 | (-1;0) | (0;1) | (1; ) | ( ;¥) |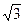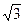
| y¢ | - | + | + | + | + | - |
     y |