Конечно-разностный аналог дифференциального уравнения неустановившейся одномерной фильтрации жидкости с единичными коэффициентами (вывод)

Рассмотрим однородный пласт, в к-м происходит одномерная фильтрация несжимаемой жидкости. Для этого случая ур-е нестац. Фильтрации имеет вид: ¶²Р/¶х²=(1/c)׶Р/¶t +q (1)

c=k×K/(mm)

где К – объемный модуль упругости

Введем безразмерные величины:

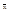=х/L; =P/P_н; q=c×t/L²; (2)

x= 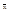×L;Р= ×P_н; t=q×L²/c; (3)

Подставим (3) в (1):

¶²Р/¶х²= 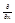(¶( ×P_н)/¶x)=(P_н/L²)* ¶² /¶ 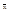² (4)

¶Р/¶t=(c×P_н/L²)׶ /¶q (5)

(Р_н/L²)׶² /¶ 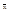²=(c×Р_н/c×L²)¶ /¶q+ Р_н×f/L²; f=q×L²/P_н; q=P_н×f/L². (6)

¶² /¶ 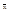²=¶ /¶q+f (7).

В дальнейшем знак « » уберем, но будем иметь ввиду, что это те же безразмерные величины.

¶²Р/¶х²=¶Р/¶q+f (7')

Разложение в ряд Тейлора:

Р(х)=Р(а)+Р'(а)(х-а)+Р''(а)(х-а)²/2!+…(8)

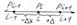
Мы рассматриваем точку i, в которой давление известно Р_i. Нас интересует Р_i+1 или Р_i-1

Р_i+1=P_i+P_i'Dx+P_i''(Dx)²/2!+P_i'''(Dx)³/3!+… (9)

Р_i-1=P_i-P_i'Dx+P_i''(Dx)²/2!-P_i'''(Dx)³/3!+… (10). Из (9) найдем первую производную:

Р_i'=(Р_i+1-Р_i)/Dx-P_i''×Dx/2!+P_i'''×(Dx)²/3!-… (11)

Р_i'=(Р_i+1-Р_i)/Dx-0(Dx) (12)

где 0(Dx) – остаточный член первого порядка малости относительно Dx. Из (10)-аналогично:

Р_i'=(Р_i-Р_i-1)/Dx+0(Dx) (13)

Складывая (12) и (13):

Р_i'=(Р_i+1-Р_i-1)/(2×Dx)+0(Dx)² (14)

где 0(Dx)² - остаточный член второго порядка малости относительно Dx.

Сложим (9) и(10):

Р_i+1+ Р_i-1=2Р_i+2 P_i''(Dx)²/2!+4 P_i^IV(Dx)⁴/4!+… (15)

Р_i''=(Р_i-1-2×Р_i+Р_i+1)/(Dx)²+0(Dx)² (16)

По времени введем шаг Dt= τ. k – номер временного узла.

¶P/¶q» Р_k'= (P_k-P_k-1)/t+0(t); Dq=t (17)Явная и неявная конечно-разностная схема.

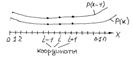
Р(к-1)-распределение Р на момент времени (к-1).

Внутренних узлов всего (n-1) и 2 граничных узла 0 и n. Производная в выражении (16) может быть записана для (к-1) временного слоя:

(Р_i-1,k-1-2×P_i,k-1+P_i+1,k-1)/(Dx)²=(P_i,k-P_i,k-1) / t + f_i,k (18) – конечно-разностное уравнение.

Известны: Р_i-1,k-1; Р_i,k-1; Р_i+1,k-1. f_i,k – плотность стока (источника) задана.

(18) соответствует явной конечно-разностной схеме, поскольку каждое уравнение содержит одно неизвестное давление P_i,k. Если записать (18) для k-го временного слоя:

(Р_i-1,k-2×P_i,k+P_i+1,k)/(Dx)²=(P_i,k-P_i,k-1)/t+f_i,k (19) - соответствует неявной конечно-разностной схеме, в к-й (n-1)+2=n+1 уравнений с n+1 неизвестных Р. В каждом уравнении (19) содержится 3 неизвестных.

Для решения ур-й типа (19) составляется система уравнений из n+1 ур-й с n+1 неизвестными. Решается такая система на каждом временном уровне методом Гаусса или методом прогонки.

Применение явной схемы возможно при t£(Dх)²/2 – усл-е обеспечивающее сходимость. Неявная схема не требует таких ограничений.

7 (35) Решение системы конечно-разностных уравнений методом прогонки (для случая неустановившейся плоскопараллельной фильтрации жидкости в пласте с еди­ничными коэффициентами

(Pi-1,k-1- 2Pi,k-1+ Pi+1,k-1)/(∆x)2=(Pi,k- Pi,k-1)/τ+fi,k, (1), где (Pi-1,k-1, Pi,k-1, Pi+1,k-1-известны) - явная конечно-разностная схема.

(Pi-1,k- 2Pi,k+ Pi+1,k)/(∆x)2= (Pi,k- Pi,k-1)/ τ+fi,k, (2)-неявная схема, i=1,n-1.

Составляя систему ур-й по неявной схеме, получаем (n+1) ур-е для внутренних узлов с (n+1) неиз-ми давлениями. Чтобы сделать систему замкнутой записывают систему при (i=0,i=n) граничных условиях. Итак, записывая производные на границах в виде:

А) на левой границе (i=0): ¶Р/¶х (3)

(Р1,к-Р0,к)/∆х=0 (4)–конечно-разностное уравнение производной (3);

Б) на правой границе (i=n): ¶Р/¶х (5)

Рn,к-Р(n-1),к)/∆х=0(6)-конечно-разностное уравнение производной (5).

Из (4) следует Р0,к= Р1,к (4а). Из (6) следует Р(n-1),к= Рn,к (6а). Итак, мы имеем замкнутую систему. Ее решают методом прогонки значений систем конечно-разностных схем неявн. ур-й.

Для i=1:(P2,k- 2P1,k+ P0,k)/(∆x)2= (P1,k- P1,k-1)/τ+f1,k (7). С учетом (4а) можно записать: (P2,k- P1,k)/(∆x)2= (P1,k- P1,k-1)/τ+f1,k (8)

Р1,к=[Р2,к+(∆x)2(P1,k-1- τ f1,k)/τ ] / [1 + (∆x)2/τ] (9)

Обозначим:А1,к=1/(1+(∆x)2/τ); С1,к=((∆x)2/τ)/(1+(∆x)2/τ))*(Р1,к-1-τ*f1,к) (10).

Р1,к=А1,кР2,к+С1,к (11).

Аналогично можно показать:

Для i=2: Р2,к=А2,кР3,к+С2,к (12).

А2,к=1/(2-А1,к+(∆x)2/τ), ,….(29)

С2,к={С1,к+(∆x)2 *(Р2,к-1-τ*f2,к) /τ }/(2- А1,к+(∆x)2/τ) (13).

Для любой внутренней точки i: Рi,к=Аi,кР(i+1),к+Сi,к (14).

Аi,к=1/(2-Аi-1,к+(∆x)2/τ), ,….(31)

Сi,к={Сi-1,к+(∆x)2 *(Рi,к-1-τ*fi,к) /τ }/(2- Аi-1,к+(∆x)2/τ) (15).

Для i=n-1: Рn-1,к=Аn-1,кРn,к+Сn-1,к (16).

С учетом (6а) получим: Рn-1,к= Сn-1,к /(1-Аn-1,к) (17).

Коэф-ты А и С наз. прогоночными коэф-ми. Они не содержат неизвестных давлений и могут быть вычислены самостоятельно. Прогоночные коэф-ты вычисляются в порядке возрастания координального индекса i (слева на право). После вычисления прогоночных коэф-ов вычисляются давления в узловых точках в порядке убывания индекса i , т.е. справа налево. Так реализуется метод прогонки. В большинстве координатных узлов f1,k=0. f1,k> или<0 в тех местах, где имеются скважины добывающие или нагнетательные.

8.Система размещения скважинРациональное размещение скв-н на площади г-носности имеет большое значение. Сетка размещения скв-н существенно влияет на все технико-экономические показатели разр-ки мест-я и обустройства промысла. Рацион-я система размещения скв-н обосновывается технико-экономическими расчетами.

Существуют следующие системы размещения скв-н:

1. Равномерное размещение по квадратной или треугольной сетке.

2. Разм-е скв-н в виде кольцевых батарей или цепочек.

3. Размещение скв-н в центральной части залежи.

4. Размещение скв-н в виде кустов.

5. Неравномерное размещение скв-н.

Под равномерной сеткой понимается такая система размещения скв-н на площади газоносности, когда в пр-се разр-ки не образуется общей депрессионной воронки, т.е. Р_пл вдали от каждой скв-ны примерно одинаковы и близки к среднему Р_пл. Изменение дебитов г-х скв-н опр-ся изменением во времени среднего Р_пл по залежи в целом.

Геометрически равномерное размещение скв-н на площади газоносности удовлетворяет отмеченному условию лишь при достаточной однородности пласта по коллекторским свойствам. В случае существенной неоднородности пласта под равномерной сеткой размещения г-х скв-н можно понимать такую, при к-й приближенно выполняется соотношение:

q₁/(αW₁)=q₂/(αW₂)=…=q_n/(αW_n) (1)

где q_i - дебит i-й скв-ны; αW_i- газонасыщенный объем дренирования i-й скв-ны. При переменных во времени дебитах в (1) подставляются знач-я соотв-х добытых кол-в г по каждой скв-не.

С вводом мест-я в разр-ку большинство разведочных скв-н переводится в добывающие. Размещение разведочных скв-н может значительно влиять на систему размещения добывающих скв-н. Необходимое число г-х скв-н для добычи г, с течением времени увеличивается. При выборе, равномерной системы размещения скв-н сетку скв-н устанавливают исходя из необходимости размещения на площади г-носности потребного проектного числа скв-н на определенный момент (на конец периода постоянной добычи г или на конец бескомпрессорного периода).

Равномерное размещение скв-н рекомендуется при разр-ке мест-й в условиях ГР и однородности продуктивного пласта по коллекторским св-вам. Преимущества:большие дебиты; минимальное число необх-х скв; продолжительный период бескомпрессорной экспл-ии; увеличиваются продолжительность и эффективность работы УНТС газа; наиболия простая схема; расчеты показателей разработки просты и более разработаны. Недостатки:увеличивается протяженность г-сборных сетей и промысловых коммуникаций; вусловиях ВНР будут интенсивнее обводняться скв. и местор.

Необходимость размещения скв-н цепочкой вызвана тем, что мест-е сильно вытянуто в плане. Размещение скв-н в виде цепочки исп-но также при создании и эксплуатации нек-ых подземных хранилищ г.

Размещение скв-н в виде кольцевых батарей или цепочек исп-ся при проектировании систем разр-и ГКМ с ППД закачкой сухого г или воды.

При размещении скв-н в виде кольцевых батарей или цепочек быстрее падают P_з, Р_у и дебиты скв-н, раньше требуется ввод дополнительных скв-н для разр-и мест-я. Газосборные системы и промысловые коммуникации при рассматриваемой системе размещения отличаются компактностью.

Скв-ны, подключаемые к УКПГ, размещаются на площади сравнительно небольшого радиуса. В рез-те создаются условия для безгидратной эксплуатации системы сбора г. Ускоряет освоение мест-я, сокращает капитальные вложения в систему обустройства промысла.

Целесообразно размещение добывающих скв-н в наиболее продуктивных зонах мест-й (центральной, купольной). Центральная часть мест-я разбуривается кустами скв-н (в одном кусте несколько скв-н, расположенных друг от друга на расстоянии 50-70 м), расстояние м/у кустами около 1,5 км.

Продлевается период безводной эксплуатации скв-н. Нередко коллекторские свойства пласта ухудшаются к периферии мест-я. Поэтому размещение скв-н в более продуктивной части мест-я обеспечивает вначале большие дебиты.

Существует оптимальная зона разбуривания, обеспечивающая наилучшие технико-экономические показатели разр-и мест-я и обустройства промысла.