Практичне заняття 6. дискретна випадкова

ВЕЛИЧИНА

Приклад. Маємо 4 заготівки для виготовлення деталей. Ймовірність виготовлення придатної деталі дорівнює 0,75. Знайти закон розподілу випадкової величини Х – кількість заготівок, що їх буде використано для виготовлення придатної деталі. Знайти 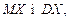а також імовірність того, що із цих заготівок буде виготовлено стандартну деталь.

Розв’язання. Подамо закон розподілу для випадкової величини Х у табличній формі. Очевидно, що випадкова величина може набувати значень 1, 2, 3, 4. Значення Х = 1, буде тоді, коли з першої заготівки виготовлено стандартну деталь, а ймовірність цього дорівнює 0,75. Випадкова величина набуває значення 2, якщо з першої заготівки виготовлено браковану деталь, а з другої — придатну. За теоремою множення імовірностей ймовірність цієї події 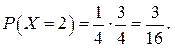Аналогічно, Х = 3, якщо деталі, виготовлені з першої та другої заготівок, браковані, а деталь, яку виготовлено з третьої заготівки – придатна. 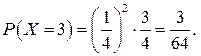Нарешті, Х = 4, якщо деталі, виготовлені з перших трьох заготівок, браковані. 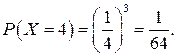Запишемо закон розподілу:

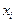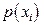	0,75	0,1875	0,046875	0,15625

Легко перевірити, що сума ймовірностей у законі розподілу дорівнює 1. Знайдемо математичне сподівання та дисперсію випадкової величини за наведеними щойно формулами.

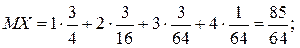
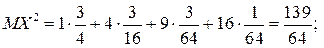
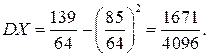
Якщо подія А – «із чотирьох заготівок виготовлено одну придатну деталь», то

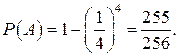
Приклад. Побудувати закон розподілу ймовірностей дискретної випадкової величини 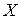. Знайти 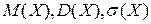, функцію розподілу та її графік.

В кишені лежать 5 монет номіналом 5 копійок і 9 монет номіналом 25 копійок. Навмання беруть дві монети.

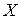– число монет номіналом 5 копійок.

Розв’язання.Дискретна випадкова величина 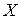може набувати значень 0, 1, 2. Знайдемо ймовірність того, що серед навмання взятих двох монет 0, 1, 2 монет номіналом 5 копійок, і занесемо одержані дані в таблицю.

Для знаходження відповідних ймовірностей використаємо класичне означення ймовірності події.

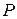(„0 п’ятаків”)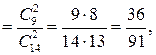

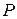(„1 п’ятак”)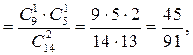

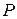(„2 п’ятаки”)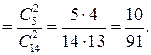

Отже, закон розподілу ймовірностей дискретної випадкової величини 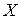має вигляд:

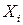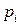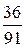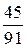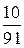Математичне сподівання дискретної випадкової величини 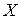обчислюється за формулою:

. .

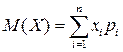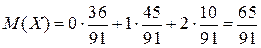Дисперсія

.

.

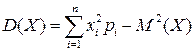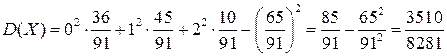Середнє квадратичне відхилення

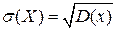
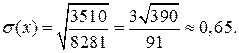
Приклад. Радист передає повідомлення, доки не передасть, але не більше трьох раз. Ймовірність спотворення повідомлення за першим разом – 0,2, за другим і третім 0,1. 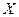– число спроб радиста.

ПРАКТИЧНЕ ЗАНЯТТЯ 7. НЕПЕРЕРВНА ВИПАДКОВА

ВЕЛИЧИНА

Приклад. Закон неперервної випадкової величини Х задано у вигляді:

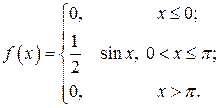
Знайти F(x) і побудувати графіки функцій f (x), F(x). Обчислити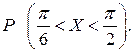

Розв’язання.

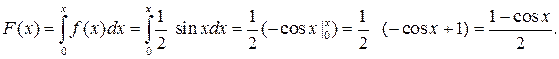
Отже, функція розподілу ймовірностей буде така:

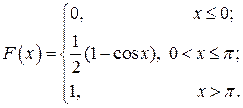
Графіки функцій f (x), F(x) зображені відповідно на рис. 1 і 2.

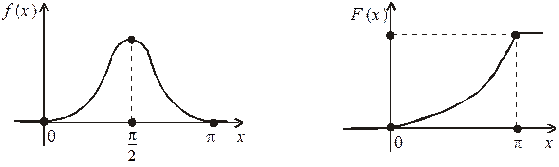
Рис. 1 Рис. 2

Імовірність події .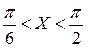

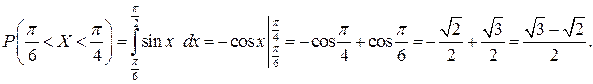
Приклад. За заданою щільністю ймовірностей

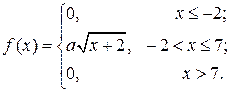
знайти значення сталої а та функцію F(x). Побудувати графіки функцій f(x), F(x).

Розв’язання. Значення сталої а визначаємо з умови нормування:

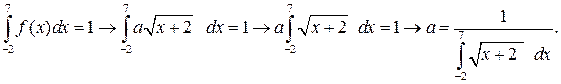
Тут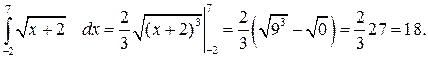

Отже,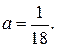

При знайденому значенні а щільність імовірностей

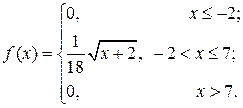
Функція розподілу ймовірностей визначається так:

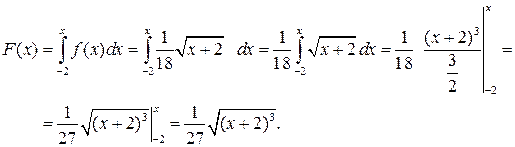
Отже,

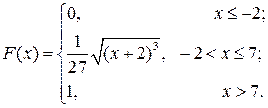
Графіки функцій f(x), F(x) зображені відповідно на рис. 3 і 4.

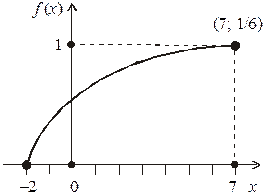
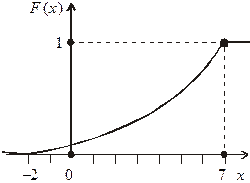
Рис. 3 Рис. 4