Определение предела последовательности
Число 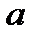 называется пределом последовательности
называется пределом последовательности 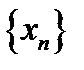
(11.1) 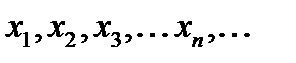
(пределом переменной 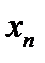 или пределом функции
или пределом функции 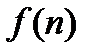 ), если каково бы ни было наперед заданное положительное число
), если каково бы ни было наперед заданное положительное число 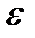 , всегда можно найти такое натуральное число
, всегда можно найти такое натуральное число 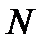 [4], что для всех членов последовательности с номерами
[4], что для всех членов последовательности с номерами 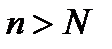 будет выполнятся неравенство
будет выполнятся неравенство
(11.2) 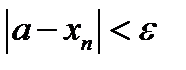
Это неравенство равносильно таким двум неравенствам:
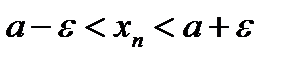
Число 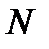 зависит, вообще говоря, от выбранного
зависит, вообще говоря, от выбранного 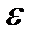 .
.
Если уменьшить число 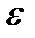 , то соответствующий ему номер
, то соответствующий ему номер 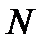 увеличится.
увеличится.
Для последовательности (или для переменной 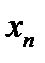 ) необязательно иметь предел, но если этот предел есть, то он единственный.
) необязательно иметь предел, но если этот предел есть, то он единственный.
Если число 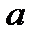 есть предел последовательности
есть предел последовательности 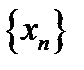 с общим членом
с общим членом 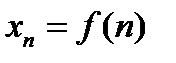 или переменной величины
или переменной величины 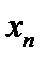 , то это символически записывается так:
, то это символически записывается так:
(11.3) 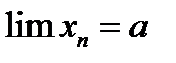 .
.
Вместо записи (11.3) употребляется также запись
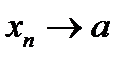
которая читается так: « 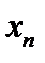 стремится к
стремится к 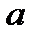 ».
».
В том случае, когда переменная величина 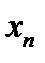 (последовательность (11.1) имеет предел, равный
(последовательность (11.1) имеет предел, равный 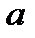 , говорят, что эта переменная величина или что последовательность
, говорят, что эта переменная величина или что последовательность 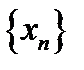 сходиться к
сходиться к 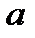 .
.
Последовательность, не имеющую предела, называют расходящейся.
Переменная величина 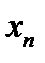 может стремиться к своему пределу разными способами:
может стремиться к своему пределу разными способами:
1) Оставаясь меньше своего предела,
2) Оставаясь больше своего предела,
3) Колеблясь около предела и
4) Принимая значения, равные своему пределу.
Выбор числа 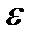 произволен, не после того как оно выбрано, никаким изменениям в дальнейшем оно не должно подвергаться.
произволен, не после того как оно выбрано, никаким изменениям в дальнейшем оно не должно подвергаться.
Задача 11.1
Доказать, что последовательность с общим членом 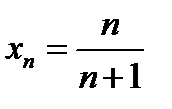 имеет предел, равный 1.
имеет предел, равный 1.
Решение.
Выберем произвольно положительное число 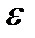 и покажем, что для него можно определить такое натуральное число
и покажем, что для него можно определить такое натуральное число 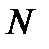 , что для всех номеров
, что для всех номеров 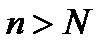 будет выполнено неравенство (11.2), в котором надо взять
будет выполнено неравенство (11.2), в котором надо взять 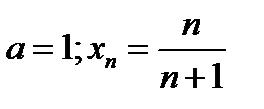 , т.е. неравенство
, т.е. неравенство
(11.4) 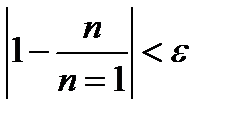 .
.
После приведения ошибок к общему знаменателю получим
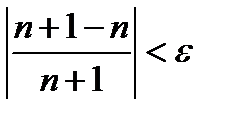 , или
, или 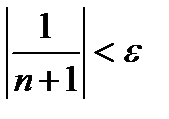 .
.
Но если 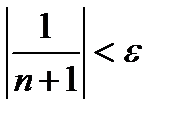 то и
то и 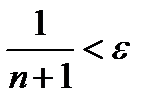 . Из последнего неравенства следует, что
. Из последнего неравенства следует, что 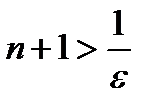 [5],
[5], 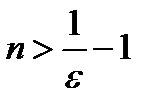 .
.
Значит, если номер 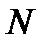 больше, чем
больше, чем 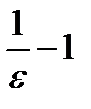 , то неравенство (11.4 )будет выполняться. Теперь надо решить вопрос о числе
, то неравенство (11.4 )будет выполняться. Теперь надо решить вопрос о числе 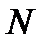 , о котором идет речь в определении. За число
, о котором идет речь в определении. За число 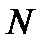 можно принять наибольшее целое число, содержащееся в числе
можно принять наибольшее целое число, содержащееся в числе 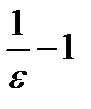 .
.
Наиболее целое число, содержащееся в числе 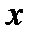 , обозначается знаком
, обозначается знаком 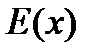 .
.
На основании этого наиболее целое число, содержащееся в числе 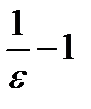 , надо обозначить так:
, надо обозначить так:  .
.
Итак, можно принять
(11.5) 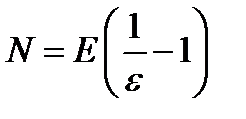
(предполагается, что 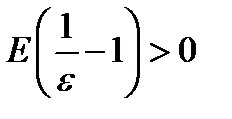 , иначе
, иначе 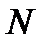 не будет натуральным и его надо брать равным 1).
не будет натуральным и его надо брать равным 1).
Заключение:
По произвольно заданному положительному числу мы нашли такое натуральное число 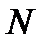 , что для всех номеров
, что для всех номеров 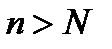 неравенство (11.4) действительно выполняется, а этим и доказано, что 1 является пределом последовательности с общим членом
неравенство (11.4) действительно выполняется, а этим и доказано, что 1 является пределом последовательности с общим членом
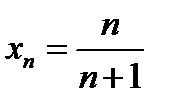 .
.
Теперь приведенные вычисления проиллюстрируем числовым примером.
Пусть, например, 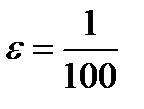 , Тогда при
, Тогда при 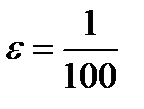 получим из (11.5)
получим из (11.5)
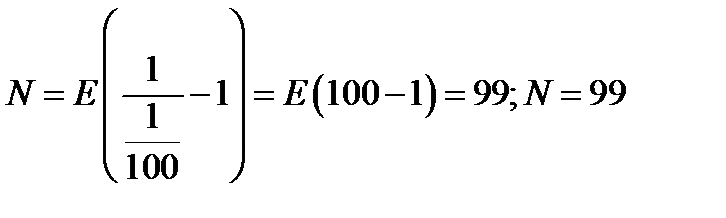
Таким образом, для членов последовательности с номером большим чем 99, выполняется неравенство
(11.6) 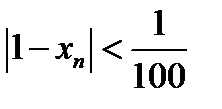 ,
,
Пусть 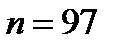 ; тогда, так как
; тогда, так как 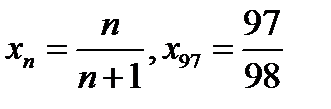 ,
,
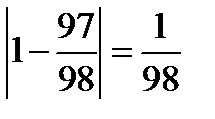 , а
, а 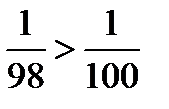 ;
;
Если 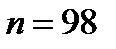 , то
, то
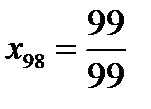 , и
, и 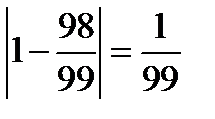 ;
; 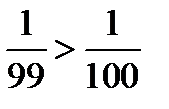 .
.
Из этих расчетов видно, что когда члена последовательности меньше 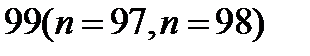 неравенство (11.6) не выполняется: вместо того чтобы
неравенство (11.6) не выполняется: вместо того чтобы 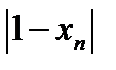 была меньше
была меньше 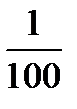 , мы получили, что
, мы получили, что 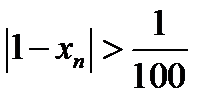 . Если взять
. Если взять 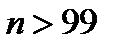 , т.е., например,
, т.е., например, 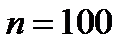 тогда
тогда 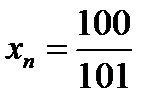 и
и 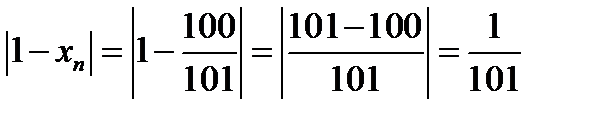 , а
, а 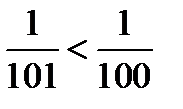 . Неравенство (11.6) будет выполняться для всех номеров
. Неравенство (11.6) будет выполняться для всех номеров 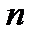 , которые больше, чем 99. Так как
, которые больше, чем 99. Так как 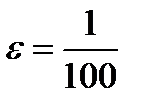 , а
, а 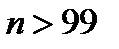 , то все члены последовательности, начиная с сотого, будут лежать на интервале
, то все члены последовательности, начиная с сотого, будут лежать на интервале 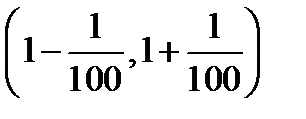 , т.е на интервале (0,99; 1,01) (теперь возьмите для
, т.е на интервале (0,99; 1,01) (теперь возьмите для 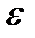 значение, меньше
значение, меньше 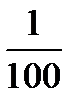 , например,
, например, 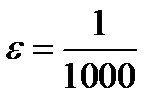 . Найдите
. Найдите 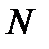 и убедитесь, что оно увеличивается).
и убедитесь, что оно увеличивается).
Полученный результат можно записать так: 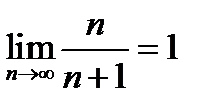 .
.
Иначе можно сказать, что последовательность 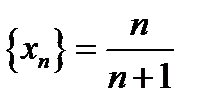 сходиться к 1.
сходиться к 1.
Мы употребили запись 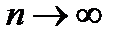 , которую следует понимать так: переменная величина
, которую следует понимать так: переменная величина 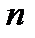 становиться все большей и большей и не существует предела для ее возрастания.
становиться все большей и большей и не существует предела для ее возрастания.
Какое бы большое число мы не задали, 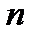 в процессе своего возрастания его превзойдет. Для того, чтобы кратко описать этот характер изменения
в процессе своего возрастания его превзойдет. Для того, чтобы кратко описать этот характер изменения 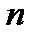 , принято говорить «
, принято говорить « 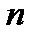 стремиться к бесконечности» и записывать это так
стремиться к бесконечности» и записывать это так 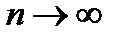 . Символ
. Символ 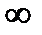 произноситься «бесконечность» и применяется для сокращенной записи слова «бесконечность».
произноситься «бесконечность» и применяется для сокращенной записи слова «бесконечность».
Символ 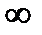 ни в коем случае не может рассматриваться как число, а потому бессмысленной является запись
ни в коем случае не может рассматриваться как число, а потому бессмысленной является запись 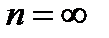 ,так как
,так как 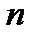 может равняться числу и не может быть равно символу, введенному только для сокращения записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
может равняться числу и не может быть равно символу, введенному только для сокращения записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
Очевидно, что последовательность 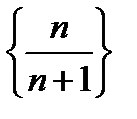 может быть записана так:
может быть записана так:
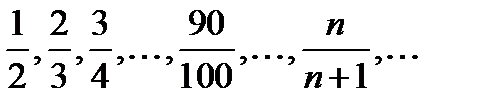
и легко усмотреть, что она стремиться к своему пределу 1, возрастая и оставаясь меньше 1.
Задача 11.2
Доказать, что последовательность с общим членом 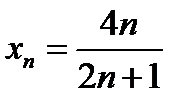 имеет предел, равный 2.
имеет предел, равный 2.
Решение.
Повторим подробно все рассуждения, приведенные в предыдущей задаче. Вберем произвольно положительное число 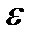 и покажем, что для него можно подобрать такое число
и покажем, что для него можно подобрать такое число 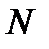 , что для всех значений номера
, что для всех значений номера 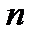 , больших этого числа
, больших этого числа 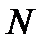 , будет выполняться неравенство (11.2). в котором надо взять
, будет выполняться неравенство (11.2). в котором надо взять 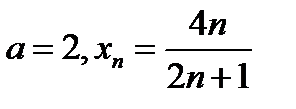 , т.е. будет выполняться неравенство
, т.е. будет выполняться неравенство
(11.7) 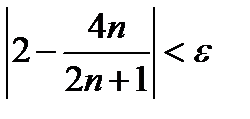 .
.
Из этого неравенства после приведения в скобках к общему знаменателю получаем
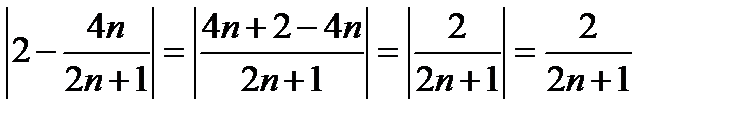 ,
,
И неравенство (11.7) запишется так: 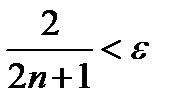 .
.
Отсюда следует, что 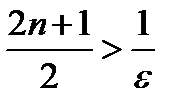 (см. сноску на стр. 272) или
(см. сноску на стр. 272) или 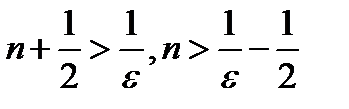 .
.
Таким образом, если номер 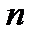 больше, чем
больше, чем 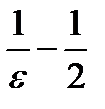 , то неравенство (11.7) будет выполняться.
, то неравенство (11.7) будет выполняться.
За 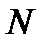 примем небольшое целое число, содержащееся в числе
примем небольшое целое число, содержащееся в числе 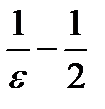 , т.е.
, т.е.
(11.8) 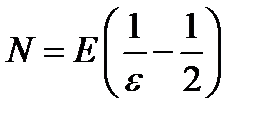 .
.
Таким образом, мы сумели по произвольно заданному положительному 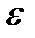 определить такое натуральное
определить такое натуральное 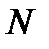 , что неравенство (11.7) выполняется для всех номеров
, что неравенство (11.7) выполняется для всех номеров 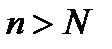 . Этим и доказано, что 2 есть предел последовательности с общим членов
. Этим и доказано, что 2 есть предел последовательности с общим членов 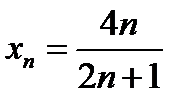 (предполагается, что
(предполагается, что 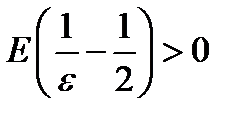 , так как иначе
, так как иначе 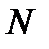 не будет натуральным членом. Если
не будет натуральным членом. Если 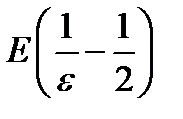 окажется отрицательным то следует взять
окажется отрицательным то следует взять 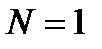 ).
).
Теперь, чтобы лучше уяснить приведенные рассуждения, приведем числовой пример: выбрано 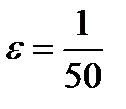 . Тогда из (11.8) следует, что
. Тогда из (11.8) следует, что
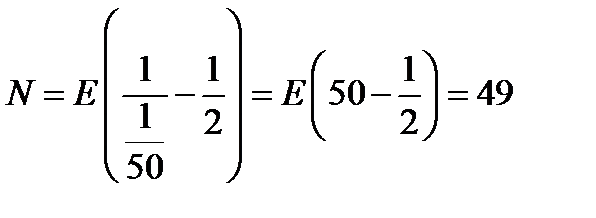 .
.
так как наибольшее целое число содержащееся в 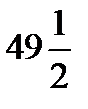 , есть 49.
, есть 49.
Значит, для всех номеров 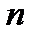 , больших, чем 49 при
, больших, чем 49 при 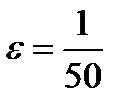 , неравенство (11.7) будет выполняться. Начиная с пятидесятого члена все члены последовательности будут лежать в интервале
, неравенство (11.7) будет выполняться. Начиная с пятидесятого члена все члены последовательности будут лежать в интервале 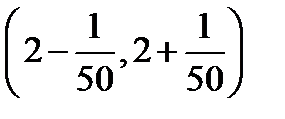 , т.е в интервале (1,98;2,0 2). Убедимся сначала, что при
, т.е в интервале (1,98;2,0 2). Убедимся сначала, что при 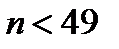 неравенство (11.7) не выполняется. Пусть, пример,
неравенство (11.7) не выполняется. Пусть, пример, 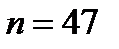 . Тогда, так как
. Тогда, так как 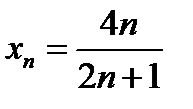 , получим, что
, получим, что 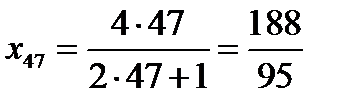 и левая часть неравенства (11.7)
и левая часть неравенства (11.7) 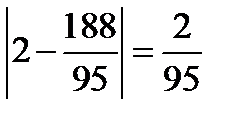 .
.
На основании (11.7) 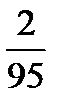 должно быть меньше, чем
должно быть меньше, чем 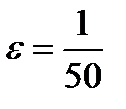 , а фактически
, а фактически 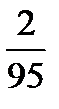 не меньше
не меньше 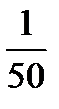 , а больше
, а больше 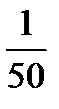 и, значит, неравенство (11.7) не выполняется.
и, значит, неравенство (11.7) не выполняется.
При 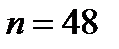 имеем
имеем 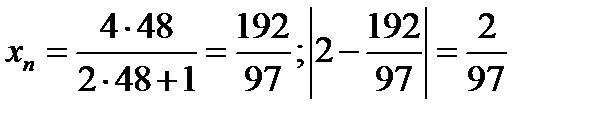 и опять неравенство (11.7) не выполняется, т.к и
и опять неравенство (11.7) не выполняется, т.к и 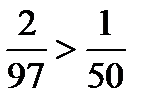 , а не меньше
, а не меньше 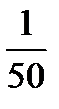 .
.
Если же взять, например, 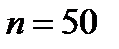 то
то 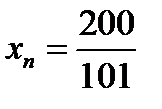 и
и 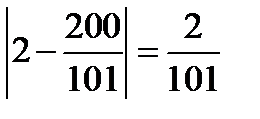 , а
, а 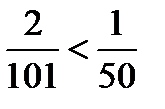 , и неравенство (11.7) выполнено. Так будет и для всех номеров
, и неравенство (11.7) выполнено. Так будет и для всех номеров 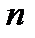 , которые больше, чем 49.
, которые больше, чем 49.
Теперь примите, за 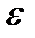 число , меньше, чем
число , меньше, чем 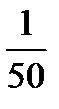 , например
, например 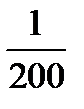 , и убедить , что
, и убедить , что 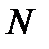 увеличивается.
увеличивается.
Итак, 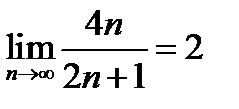 (можно сказать иначе: последовательность
(можно сказать иначе: последовательность 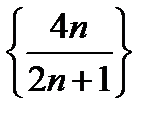 сходится к 2).
сходится к 2).
Замечание 1. В решениях двух задачах мы находили наименьший номер 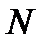 , фигурирующий в определении предела последовательности, такой, что начинается с него, неравенство (11.2) выполняется. Однако учащийся должен уяснить, что
, фигурирующий в определении предела последовательности, такой, что начинается с него, неравенство (11.2) выполняется. Однако учащийся должен уяснить, что
1) Если это неравенство выполняется, начиная с номера 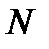 , то оно будет выполняться и подавно при всех номерах
, то оно будет выполняться и подавно при всех номерах 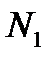 , больших чем
, больших чем 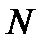 ;
;
2) Заданием число 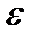 номер
номер 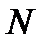 определяется неоднозначно и
определяется неоднозначно и
3) Для доказательства того, что 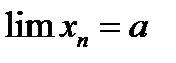 , вовсе нет необходимости среди всех номеров
, вовсе нет необходимости среди всех номеров 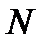 искать наименьший. Так, в задаче 11.1, установив, что неравенство (11.4) выполняется для всех
искать наименьший. Так, в задаче 11.1, установив, что неравенство (11.4) выполняется для всех 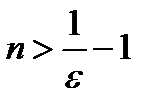 , мы могла дальше не вести никаких рассуждений.
, мы могла дальше не вести никаких рассуждений.
Замечание 2. Выше было указано что если последовательность имеет предел, то этот предел – единственный: двух различных пределов последовательность иметь не может.
В последней задаче мы доказали, что пределом последовательности 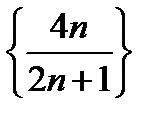 является 2.
является 2.
Покажем, что, например, число 3 не может быть пределов этой последовательности.
Рассмотрим абсолютную величину разности

и решаем относительно 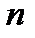 неравенство
неравенство 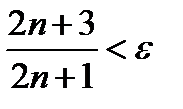 .
.
При любом целом и положительном 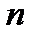 ( а номер
( а номер 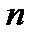 может быть только числом целым и положительным) число
может быть только числом целым и положительным) число 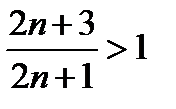 , а поэтому оно не может быть меньше произвольно заданного положительного числа
, а поэтому оно не может быть меньше произвольно заданного положительного числа 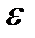 . Этим мы показали, что число 3 не может служить пределом последовательности
. Этим мы показали, что число 3 не может служить пределом последовательности 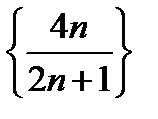 .
.
Теперь самостоятельно решите простую задачу.
Задача 11.3
(для самостоятельного решения). Доказать, что переменная 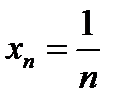 имеет предел, равный нулю (следует запомнить, что
имеет предел, равный нулю (следует запомнить, что 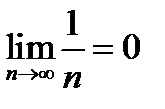 ).
).
Произносится эта запись так: «предел 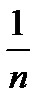 , когда
, когда 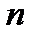 стремится к бесконечности, равен нулю». Вместо того чтобы писать
стремится к бесконечности, равен нулю». Вместо того чтобы писать 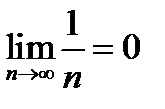 можно употребить запись
можно употребить запись 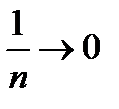 при
при 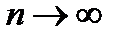 , которую следует читать как: «
, которую следует читать как: « 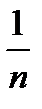 стремится к нулю при
стремится к нулю при 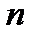 , стремящемся к бесконечности». Из того, что
, стремящемся к бесконечности». Из того, что 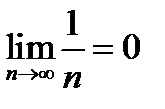 , следует, что
, следует, что 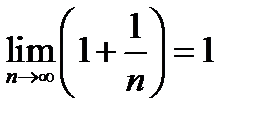 и
и 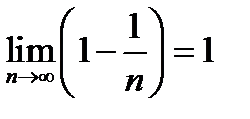 .
.
Сокращенно это можно записать так: 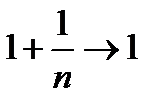 при
при 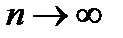 ,
, 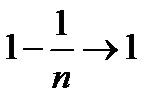 при
при 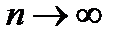 .
.
Задача 11.4
Доказать, что последовательность 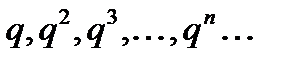 сходится к нулю, если абсолютная величина
сходится к нулю, если абсолютная величина 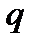 меньше 1, т. с. если
меньше 1, т. с. если 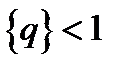 .
.
Решение.
Чтобы доказать требуемое, возьмем произвольное положительное число 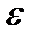 и убедимся, что можно будет определить такое
и убедимся, что можно будет определить такое 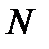 , что для номеров
, что для номеров 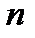 , больших
, больших 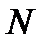 будет выполняться неравенство
будет выполняться неравенство
(11.9) 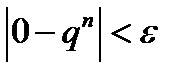
(в неравенстве (11.2) надо взять 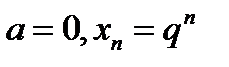 ).
).
Учитывая, что по условию 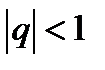 можно заключить, что
можно заключить, что 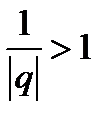 , т. е. можно полагать, что
, т. е. можно полагать, что 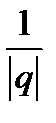 равно
равно  , где
, где  – число положительное.
– число положительное.
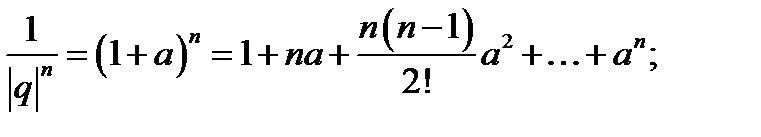

а поэтому 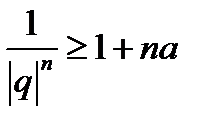 , или
, или 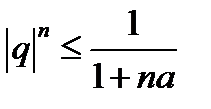 .
.
Выберем 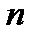 так, чтобы знаменатель дроби
так, чтобы знаменатель дроби 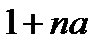 стал больше, чем
стал больше, чем 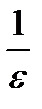 . Тогда окажется, что и подавно
. Тогда окажется, что и подавно 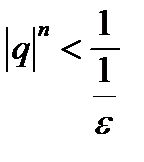 , т.е.
, т.е.  , и неравенство (11.9) будет выполняться, так как из него следует, что
, и неравенство (11.9) будет выполняться, так как из него следует, что 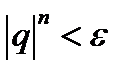 . Но если
. Но если 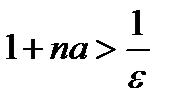 , то
, то 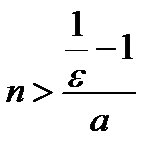 . Значит, можно в качестве
. Значит, можно в качестве 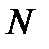 выбрать наибольшее целое число, содержащееся в числе
выбрать наибольшее целое число, содержащееся в числе 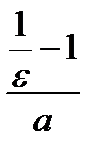 , т.е. взять
, т.е. взять 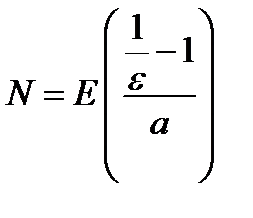 , и при этом неравенство (11.9) будет выполняться при всех номерах
, и при этом неравенство (11.9) будет выполняться при всех номерах 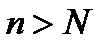 . Таим образом доказано, что
. Таим образом доказано, что 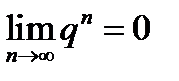 .
.
Надо заметить, что если 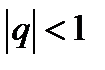 , то
, то 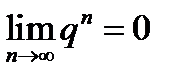 (
( 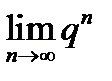 ,когда
,когда 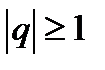 вычислен в задаче 13.1).
вычислен в задаче 13.1).
Если, например, 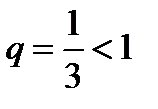 то последовательность запишется так:
то последовательность запишется так: 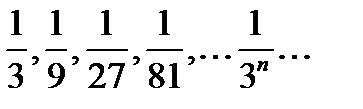 , и переменная
, и переменная 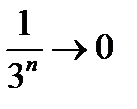 , монотонно убывая (здесь каждое следующее значение переменной меньше предыдущего).
, монотонно убывая (здесь каждое следующее значение переменной меньше предыдущего).
Если 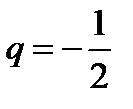 , то последовательность запишется так:
, то последовательность запишется так: 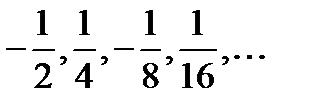 .
.
И эта последовательность, как доказано, сходиться к нулю 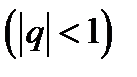 .
.
Однако здесь уже переменная величина 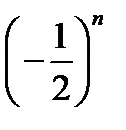 стремиться к своему пределу – нулю, применяя значения, то меньше нуля, то больше его. Можно сказать, что переменная в данном случае колеблется около нуля.
стремиться к своему пределу – нулю, применяя значения, то меньше нуля, то больше его. Можно сказать, что переменная в данном случае колеблется около нуля.
Запишем эту последовательность в виде
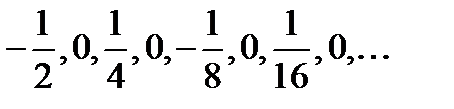
Ясно, что и эта последовательность сходиться к нулю, но теперь она содержит бесконечное множество членов, равных нулю. Это тот случай, когда переменная, стремясь к пределу, становится равной ему, причем это имеет место бесконечное множество раз.
Задача 11.5
Доказать, что последовательность 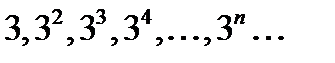 не имеет предела.
не имеет предела.
Решение.
Мы докажем требуемое, если установим, что общий член этой последовательности 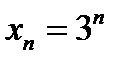 превзойдет любое наперед заданное число.
превзойдет любое наперед заданное число.
Пусть 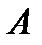 такое число. Возьмем
такое число. Возьмем 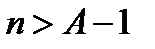 . Тогда
. Тогда 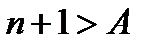 ;
; 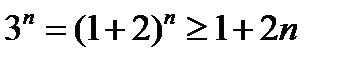 , и подавно
, и подавно 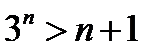 , или
, или 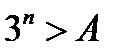 . Тем самым показано, что
. Тем самым показано, что 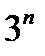 может превзойти любое число
может превзойти любое число 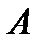 . Если бы существовал предел переменной
. Если бы существовал предел переменной 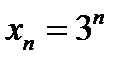 , и был равен
, и был равен 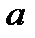 , то для любого
, то для любого 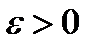 можно было бы подобрать такое
можно было бы подобрать такое 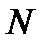 , что при номерах
, что при номерах 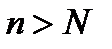 выполнялись бы неравенства
выполнялись бы неравенства 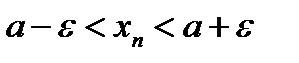 , т.е.
, т.е. 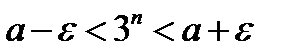 , а это противоречит доказательству, так как
, а это противоречит доказательству, так как 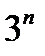 при
при 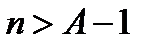 превзойдет любое число
превзойдет любое число 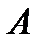 , а тем самым и число
, а тем самым и число 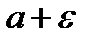 , меньше которого оно должно оставаться. Это противоречие и доказывает, что последовательность
, меньше которого оно должно оставаться. Это противоречие и доказывает, что последовательность 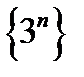 предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел.
предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел.
Задача 11.6
Доказать, пользуясь определением предела последовательности, что последовательность с общим членом 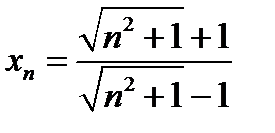 имеет предел
имеет предел 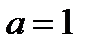 .
.
Решение.
Подставим значения и в неравенство (11.2)и получим
(11.10) 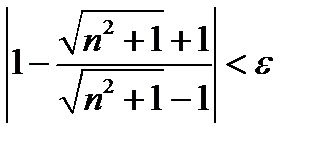 .
.
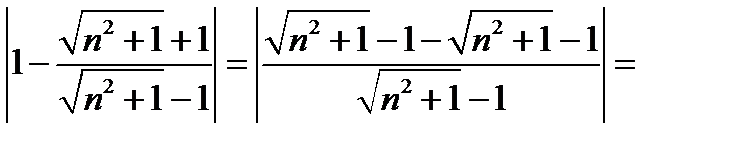
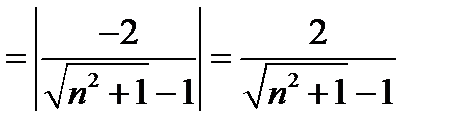 .
.
Вместо неравенства (11.10) теперь имеем неравенство 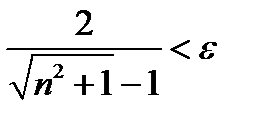 .
.
Решим это неравенство относительно 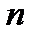 :
:
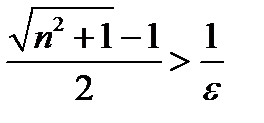 ,
, 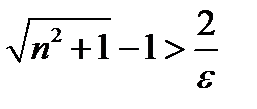 ,
, 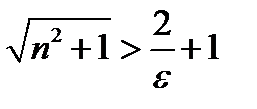 ;
;
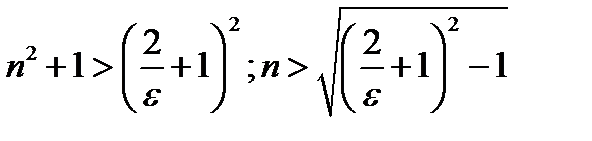 .
.
Таким образом, если 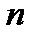 удовлетворяет последнему неравенству, то неравенство (11.10) будет выполняться при любом
удовлетворяет последнему неравенству, то неравенство (11.10) будет выполняться при любом 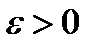 . Тем самым мы доказали, что
. Тем самым мы доказали, что 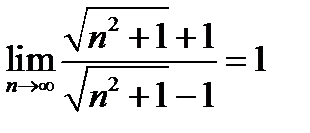 , а за
, а за 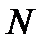 можно принять
можно принять 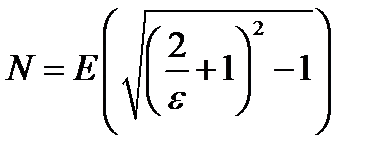 .
.
Определим из этого равенства значение 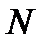 при
при 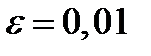 и
и 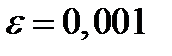 . Если
. Если 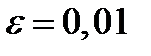 , то
, то 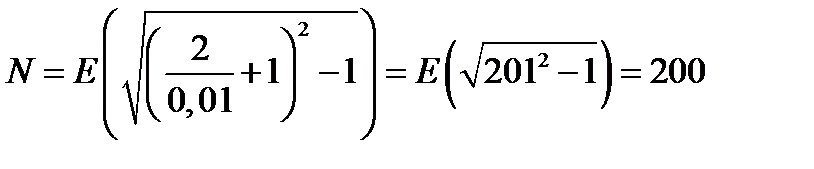 .
.
Значит, при всех номерах 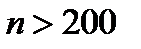 будет выполняться неравенство
будет выполняться неравенство 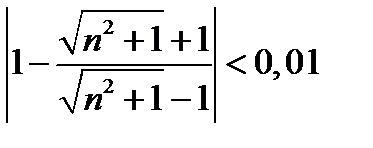 , т.е. при
, т.е. при 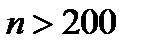 все числа заданной последовательности будут лежать на интервале (0,99;1,01). Если
все числа заданной последовательности будут лежать на интервале (0,99;1,01). Если 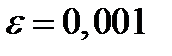 , то
, то 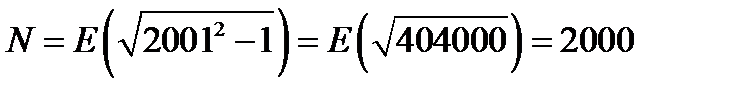 и для всех членов последовательности с номерами
и для всех членов последовательности с номерами 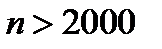 будет выполняться неравенство
будет выполняться неравенство 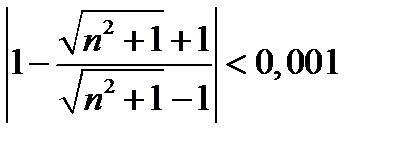 , а для номеров
, а для номеров 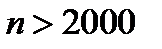 все члены последовательности будут лежать на интервале (0,999;1,001).
все члены последовательности будут лежать на интервале (0,999;1,001).
Задача 11.7
(для самостоятельного решения).Пользуясь определением предела последовательности, доказать, что
1) 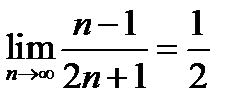 ;
;
2) 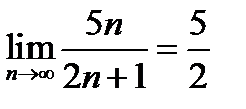 ;
;
3) 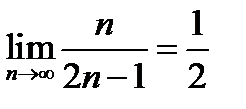 ;
;
4) 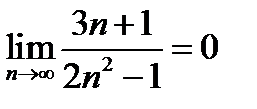 ;
;
5) 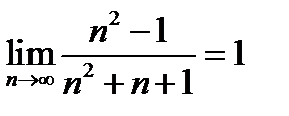 ;
;
6) 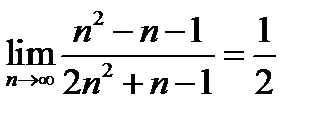 .
.
Задача 11.8
(для самостоятельного решения).Пользуясь определением предела последовательности, доказать, что
1) 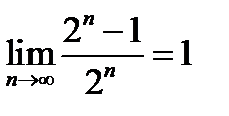 ;
;
2) 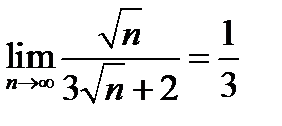 ;
;
3) 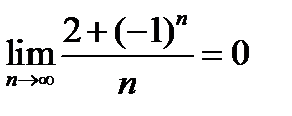 ;
;
4) 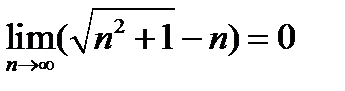 ;
;
Задача 11.9
(для самостоятельного решения). Составить последовательности: 1) возрастающую и сходящуюся к нулю; 2) убывающую и сходящуюся к 1; 3) колеблющуюся и сходящуюся к 1; 4) колеблющуюся и расходящуюся; 5) убывающую и расходящуюся.
ДВЕНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Бесконечно малые и бесконечно большие величины. Дальнейшие упражнения в определении предела последовательности.
