Решить линейные неоднородные системы

№109. №110.

№111. №112.

Решить линейную однородную систему с постоянными коэффициентами

№113. №114.

№115. .№116.

№117 . №118.

III. Вопросы по теме:

« Системы дифференциальных уравнений»

1. Что называется системой ДУ первого порядка?

2. Нормальная система ДУ, ее общий вид

3. Что является решением нормальной системы ДУ

4. Задача Коши при решении нормальной системы ДУ

5. Теорема существования и единственности решения НСДУ

6. Общее решение системы ДУ. Геометрический и механический смысл решения ДУ.

7. Интегрирование нормальной системы ДУ

8. Определение линейной однородной системы ДУ

9. Как составляется характеристическое уравнение системы? Метод решения

Таблица производных

15.

16.

Таблица основных интегралов

	Интегралы	Дифференциалы
		d(const) = 0

Тема № 2 Элементы теории поля.

Литература

1. Письменный « Конспект лекций по высшей математике» кн 2

Скалярное поле

Пространство или любая его часть, в каждой точке M которого, задана некоторая скалярная физическая величина U называется скалярным полем

Уравнение поверхности уровня

U(x,y,z) = C, где C – const,

U(x; у) = C представляет собой уравнение линии уровня поля

Производная по направлению

Определение Предел отношения приращения функции поля в направлении вектора к величине перемещения при условии, что последнее стремится к нулю, называется производной функции поля в заданном направлении

Формула для решения задач

1. Найти производную функции по направлению вектора в любой точке.

2. Найти производную функции в точке в направлении, идущем от этой точки к точке .

3. Найти производную функции в точке по направлению радиус-вектора точки .

4. Найти производную функции в точке в направлении биссектрисы первого координатного угла.

5. Найти производную функции в точке в направлении, идущем от этой точки к началу координат.

6. Найти производную функции в точке в направлении, образующем с осями координат углы соответственно в .

7. Найти производную функции в точке в направлении вектора , составляющего острые углы со всеми координатными осями.

Градиент

Определение:

Вектор, координатами которого являются значения частных производных первого порядка функции U(x,y,z) в точке M(x,y;z), называют градиентом

функции и обозначают gradU, т. е. gradU = или

gradU =

Найти градиент скалярного поля

8. в точке .

9. в точке .

10. в точке .

11. , где , .

12. Найти угол между градиентами функции а точках и .

13. Найти точку, в которой градиент функции равен

14. Найти величину и направление градиента поля в точке .

15. По какому направлению в точке скалярное поле изменяется быстрее всего и, какова максимальная скорость этого изменения?

Поток вектора

Определение:Потоком вектора а через поверхность σ называется поверхностный интеграл по площади этой поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т. е.

(1) – формула для решения задач

Рассмотрим поток вектора 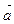(М) через замкнутую поверхность σ

(2)

16. Вычислить поток вектора 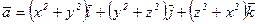изнутри поверхности куба, ограниченного плоскостями .

17. Вычислить поток данного векторного поля изнутри замкнутой поверхности .

18. Найти поток векторного поля через боковую положительную сторону поверхности пирамиды с вершиной в точке , основанием которой служит треугольник с вершинами

19. Вычислить поток вектора 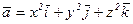изнутри полной поверхности пирамиды, ограниченной плоскостями .

20. Найти поток радиус-вектора 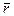через верхнюю часть плоскости заключенную в первом октанте.

21. Найти поток вектора через верхнюю часть плоскости , лежащей в первом октанте

Дивергенция

Определение

Дивергенцией (или расходимостью) векторного поля

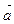{М) = Р{х\ у; z)i + Q{x\ y\ z)j + R(x\ у; z)k

в точке М называется скаляр вида и обозначается символом

div 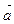(М),

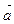div (М) =