К экзамену по высшей математике за 3 семестр
ВОПРОСЫ
1. Основные понятия теории дифференциальных уравнений.
2. Дифференциальные уравнения первого порядка. Задача Коши, теорема о существовании и единственности ее решения. Общее, частное решение (интеграл), особое решение.
3. Геометрическая интерпретация ДУ 1-го порядка. Метод изоклин.
4. Дифференциальные уравнения с разделяющимися переменными.
5. Однородные ДУ. Уравнения, сводящиеся к однородным.
6. Линейные ДУ 1-го порядка. Уравнения Бернулли.
7. Дифференциальные уравнения в полных дифференциалах.
8. Решение ДУ с помощью интегрирующего множителя.
9. ДУ высших порядков, задача Коши. Общее, частное решение. Теорема существования и единственности решения задачи Коши.
10. Дифференциальные уравнения, допускающие понижение порядка.
11. Линейные ДУ высших порядков. Теорема существования и единственности решения задачи Коши. Теорема о свойстве решений ЛОДУ.
12. Линейная независимость функций. Определитель Вронского.
13. Структура общего решения ЛОДУ высших порядков.
14. Формула Лиувилля для определителя Вронского, построенного на ФСР ЛОДУ.
15. Теорема об отыскании второго решения ЛОДУ 2-го порядка по известному первому решению.
16. ФСР ЛОДУ 2-го порядка с постоянными коэффициентами. Характеристическое уравнение.
17. ФСР ЛОДУ n-го порядка.
18. ЛНДУ. Метод вариации произвольных постоянных.
19. Структура общего решения ЛНДУ. Принцип суперпозиции решений.
20. Подбор частного решения ЛНДУ методом неопределенных коэффициентов.
21. Нормальная система ДУ. Общее решение, задача Коши, частное решение. Геометрическая и механическая интерпретация системы 2-го порядка. Фазовая плоскость.
22. Связь между ДУ n-го порядка и системой ДУ n-го порядка. Метод исключения.
23. Функции комплексного переменного. Предел, непрерывность, свойства функций, имеющих предел.
24. Показательная, тригонометрические, гиперболические, логарифмическая, общая степенная и общая показательная функции комплексного переменного.
25. Обратные тригонометрические и гиперболические ФКП.
26. Производная ФКП. Необходимые условия дифференцируемости функции в точке.
27. Достаточные условия дифференцируемости функции. Аналитические функции. Гармонические функции.
28. Геометрический смысл модуля и аргумента производной ФКП. Конформные отображения.
29. Примеры конформных отображений.
30. Интеграл от ФКП. Свойства интеграла. Интеграл с переменным верхним пределом. Теорема Мореры.
31. Интегральные теоремы Коши для односвязной и многосвязной областей.
32. Формула Коши для односвязной области.
33. Формулы Коши для производных. Бесконечная дифференцируемость аналитических функций.
34. Разложение аналитической функции в ряд Тейлора в круге. Разложение функции в ряд Лорана в кольце.
35. Нули аналитических функций. Правила определения порядка нулей.
36. Классификация особых точек ФКП. Изолированные особые точки.
37. Вычеты, их вычисление в особых точках. Вычет в бесконечно удаленной точке.
38. Основная теорема о вычетах. Теорема о сумме всех вычетов.
39. Вычисления определенных интегралов по отрезку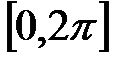 
от рациональной функции относительно 
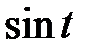и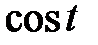 
и несобственных интегралов с бесконечными пределами от рациональных функций.
40. Леммы Жордана. Несобственные интегралы по действительной оси от функций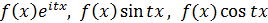 
.
41. Преобразование Лапласа. Условия на функцию - оригинал.
42. Теорема о существовании изображения и следствие из нее.
43. Изображения единичной функции, показательной, степенной, тригонометрических и гиперболических функций.
44. Линейность преобразования Лапласа, теоремы смещения и запаздывания.
45. Теорема подобия. Изображение периодического оригинала. Свертка оригиналов. Изображение свертки оригиналов (формула умножения изображений).
46. Дифференцирование и интегрирование оригинала и изображения.
47. Обратное преобразование Лапласа (формула Меллина). Вторая теорема разложения.
48. Теорема разложения для рациональных функций. Первая теорема разложения.
49. Решение ЛДУ с постоянными коэффициентами операционным методом. Формула Дюамеля и ее применение к решению дифференциальных уравнений.
Основные понятия и формулы по материалу третьего семестра
1. Теорема существования и единственности решения задачи Коши для дифференциального уравнения первого порядка.
2. Определение общего решения дифференциального уравнения первого порядка.
3. Общий вид дифференциального уравнения с разделяющимися переменными.
4. Определение однородного дифференциального уравнения первого порядка.
5. Общий вид линейного дифференциального уравнения первого порядка.
6. Общий вид дифференциального уравнения Бернулли.
7. Определение дифференциального уравнения в полных дифференциалах.
8. Уравнения, допускающие понижения порядка и методы их решения.
9. Структура общего решения линейного однородного дифференциального уравнения n-го порядка.
10. Структура общего решения линейного неоднородного дифференциального уравнения n-го порядка.
11. Условия Коши-Римана.
12. Интегральная теорема Коши для односвязной области.
13. Интегральная теорема Коши для многосвязной области.
14. Интегральная формула Коши.
15. Интегральная формула Коши для производной ФКП.
16. Нули аналитической функции. Правила определения порядка нулей.
17. Определения устранимой особой точки ФКП.
18. Определение полюса ФКП.
19. Определение существенно особой точки ФКП.
20. Правила определения порядка полюса ФКП.
21. Определение вычета ФКП в особой точке.
22. Вычисление вычета в устранимой особой точке ФКП.
23. Вычисление вычета в существенно особой точке ФКП.
24. Вычисление вычета ФКП в простом полюсе.
25. Вычисление вычета ФКП в полюсе n-го порядка.
26. Основная теорема о вычетах.
27. Определение на функцию-оригинал.
28. Теорема о существовании изображения и следствие из нее.
29. Линейность преобразования Лапласа.
30. Теорема смещения.
31. Теорема запаздывания.
32. Теорема подобия.
33. Изображение периодического оригинала.
34. Определение свертки оригиналов. Теорема Бореля.
35. Дифференцирование оригинала.
36. Интегрирование оригинала.
37. Дифференцирование изображения.
38. Интегрирование изображения.
39. Интеграл Дюамеля.
40. Формула Меллина.
41. Первая теорема разложения.
42. Вторая теорема разложения.