Анализ электрического состояния линейных

КУРСОВОЙ ПРОЕКТ

Анализ электрического состояния однофазных и трехфазных цепей

Выполнил: студент группы АИЭ113б

Волков П. А.

Проверил: ст. преподаватель

М.А. Мясоедова

КУРСК – 2012

МИНИСТЕРСТВ О СЕЛЬСКОГО ХОЗЯЙСТВА

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Курская государственная сельскохозяйственная академия имени профессора И.И.Иванова»

Кафедра «Информатики и электроэнергетики»

УТВЕРЖДАЮ

Зав. Кафедрой___________________________________________

подпись, инициалы, фамилия

«_______»_________________ 20___г.

ЗАДАНИЕ №__________

на курсовой проект (работу)

Студент__________________________________________________________код, группа _________

инициалы, фамилия

1 Тема Анализ электрического состояния однофазных и трехфазных цепей

2 Срок представления проекта к защите

«____»______________20__г.

3 Исходные данные для проектирования (научного исследования)

Задание 1

№ варианта	Е1 (В)	Е2 (В)	R1(Ом)	R2(Ом)	R3(Ом)	R4(Ом)	R5(Ом)	R6(Ом)	r01(Ом)	r02(Ом)

Задание 2

№ варианта	Um (В)	yu(град)	R1(Ом)	R2(Ом)	L1(млГн)	L1(млГн)	C(мкФ)	C (мкФ)
					79,5	127,2		79,5

Задание 3

№ варианта	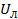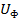В	В	Сопротивления фаз	Схема соединения
RА (Ом)	RВ (Ом)	RС (Ом)	ХLA (Ом)	ХLB (Ом)	ХLC (Ом)	ХCA (Ом)	ХCB (Ом)	ХCC (Ом)
		-	15,36	25,8	12,5	12,9	-	21,65	-	30,7	-	Y

4 Перечень разделов пояснительной записки

4.1 Содержание

4.2 Введение

4.3 Расчет линейных электрических цепей постоянного тока

4.4 Анализ электрического состояния однофазных электрических цепей переменного тока

4.5 Анализ электрического состояния трехфазных электрических цепей переменного тока

4.6 Заключение

4.7 Список использованных источников

4.8 Приложения

5 Перечень графического материала 3 л._ф. А3

Руководитель проекта (работы) _____________

подпись, дата инициалы, фамилия

Задание принял к исполнению _____________

подпись, дата инициалы, фамилия

СОДЕРЖАНИЕ

Введение………………………………………………………………………
Анализ электрического состояния линейных электрических цепей постоянного тока………………………………………………………….…
Анализ электрического состояния однофазных электрических цепей постоянного тока……………………………………………………….…….
Анализ электрического состояния трехфазных электрических цепей переменного тока………………………………………………………….....
Заключение……………………………………………………………….…..
Список использованных источников………………………………………

Введение

Теоретические основы электротехники (ТОЭ) как наука посвящена решению задач анализа и синтеза электрических цепей. К электрическим цепям относится огромное число технических устройств самого разнообразного назначения. Там, ГД речь идет об электрическом токе или электрическом напряжении, имеют дело с электрической цепью. Задача анализа состоит в качественной и количественной оценках свойств заданной электрической цепи, а задача синтеза – в построении цепи с заданными свойствами.

Современные эффективные аналитические методы анализа электрических цепей основаны в конечном счете на сочетании законов Кирхгофа, которым удовлетворяют токи и напряжения в электрических цепях, с теорией дифференциальных уравнений. Находят, естественно, широкое применение и численные методы анализы электрических цепей, в которых реализуются алгоритмы решения уравнений, связывающих между собой напряжения и токи в анализируемой цепи.

Высокий уровень развития расчетных методов теории электрических цепей и совершенство оптимальных методов их синтеза обязаны использованию применительно к соответствующим задачам фундаментальных исследований русских и советских математиков П. Л. Чебышева, Е. И. Золоторева (методы наилучшего равномерного приближения функций), А. А. Ляпунова (критерии устойчивости), Л. В. Канторовича (линейное программирование), Е. Я. Ремеза (численные методы уравнивания максимумов), а также ряда советских ученых. Работы которых способствовали развитию методов собственно теории электрических цепей (Е. В. Зелях, В. Н. Листов, М. Г. Цимбалистый и др.)

Изучение курса ТОЭ основывается на знаниях курсов физики, математики, электронных и полупроводниковых приборов и других специально-технических курсов, изучение которых или предшествует, или ведется одновременно с ними. В свою очередь, курс ТОЭ образует ту базу, на которой строится изложение последующих специально-технических курсов, как теоретико-специальных, так и аппаратурных. Именно в курсе ТОЭ вводятся основные понятия и термины, которые широко используются во всех последующих специально-технических курсах.

Анализ электрического состояния линейных

электрических цепей постоянного тока

Для электрической цепи, изображенной на рис. 1.1, выполнить сле­дующее:

1) составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

2) определить токи во всех ветвях схемы, используя метод контурных токов;

3) определить токи во всех ветвях схемы на основании метода нало­жения;

4) составить баланс мощностей для заданной схемы;

5) результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить;

6) определить ток во второй ветви методом эквивалентного генератора;

7) построить потенциальную диаграмму для любого замкнутого кон­тура, включающего обе ЭДС.

8) результаты расчетов занести в соответствующую таблицу.

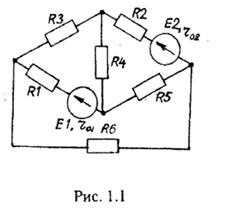
Дано: Е₁= 50 В, Е₂ = 30 В, R₁ = 53 Ом,

R₂ = 34 Ом, R₃ = 24 Ом, R₄ = 18 Ом,

R₅ = 25 Ом, R₆ = 42 Ом, r₀₁ = 1 Ом,

r₀₂ = 1 Ом.

Определить: I₁, I₂, I₃, I₄, I₅ , I₆

1) Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.

Для начала упростим схему:

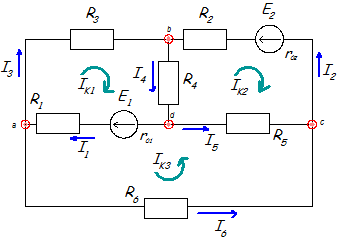
Рис.1.1 а

Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.

При расчете данным методом произвольно задаем направление токов в ветвях I₁, I₂, I₃, I₄, I₅, I₆

Составляем систему уравнений.

В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m = 6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n - 1) независимых уравнений. В нашей цепи четыре узла (a, b, c, d), значит, число уравнений

n - 1 = 4–1 = 3. Составляем три уравнения для любых 3-х узлов, например, для узлов a, b, и c .

узел а: I₁ – I₃ - I₆=0

узел b: – I₂ + I₄ - I₃=0

узел с: I₂ - I₅ – I₆=0

Всего в системе должно быть шесть уравнений. Три уже есть. Три не­достающих составляем для линейно независимых контуров. Чтобы они были

независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.

Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.

Контур abda - обход по часовой стрелке:

Е₁= I₁(R₁+r₀₁) + I₃ R₃ + I₄R₄

Контур cdbc - обход по часовой стрелке:

-- E₂ = I₂(R₂+r₀₂)--I₅R₅ -- I₄R₄

Контур acda - обход против часовой стрелки:

E₁ = I₁(R₁+r₀₁)+I₆R₆ -- I₅R₅

ЭДС в контуре берется со знаком “+”, если направление ЭДС совпадает с обходом контура, если не совпадает – знак “-”.

Падение напряжения на сопротивлении контура берется со знаком “+”, если направление тока в нем совпадает с обходом контура, со знаком “-” если не совпадает.

Мы получили систему из шести уравнений с шестью неизвестными:

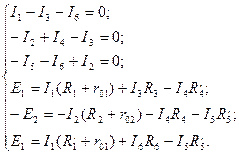
Решив систему, определим величину и направление тока во всех ветвях схемы.

Если при решении системы ток получается со знаком “-” значит его действительное направление обратно тому направлению, которым мы за­дались.

2) Определить токи во всех ветвях схемы, используя метод контурных токов.

Метод контурных токов основан на использовании только второго за­кона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи можно рассмотреть три контура-ячейки (abda, cdbc, acda) и ввести для них контурные токи I_К1, I_К2, I_К3.

Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур - ячейку, в правой части равенства алгебраически суммируются на­пряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом кон­турных токов будет следующим:

- стрелками указываем выбранные направления контурных токов I_К1, I_К2, I_К3. в контурах - ячейках. Направление обхода контуров принимаем таким же;

- составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей:

Подставляем в уравнение численные значения ЭДС и сопротивлений.

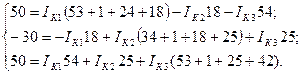
или

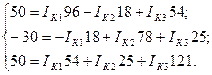
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ₁, Δ₂, Δ₃.

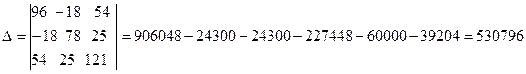
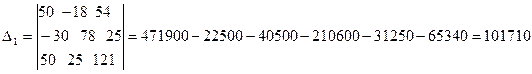
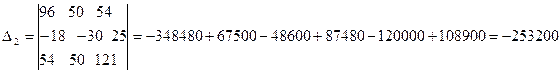
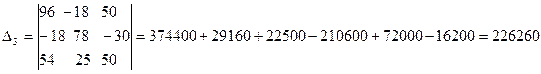
Вычисляем контурные токи:

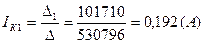
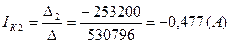
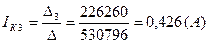
Действительные токи ветвей:

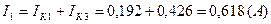
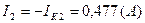
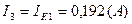
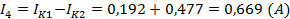
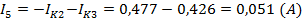
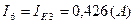
3) Определить токи во всех ветвях схемы на основании метода на­ложения.

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

а) Определяем частные токи от ЭДС E₁, при отсутствии ЭДС Е₂, т. е. рассчитываем цепь по рис. 1.2.

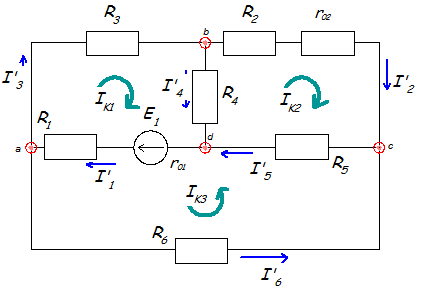
Рис. 1.2

Показываем направление частных токов от ЭДС Е₁ и обозначаем буквой I с одним штрихом (I').

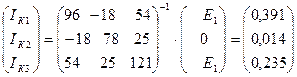
Токи в ветвях:

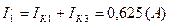
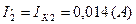
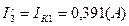
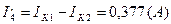
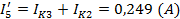
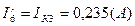
б) Определяем частные токи от ЭДС E₂ при отсутствии ЭДС Е₁,т.е. рассчитываем простую цепь по рис. 1.3.

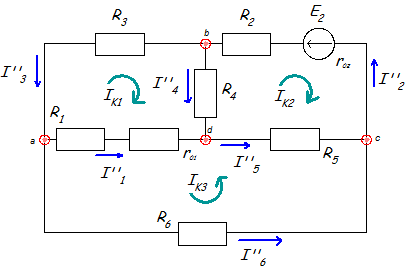
Рис.1.3

Показываем направление частных токов от ЭДС Е₂ и обозначаем их буквой I с двумя штрихами (I").

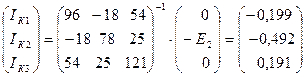
Токи в ветвях:

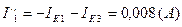
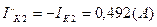
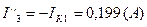
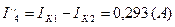
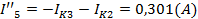
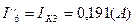
Вычисляем токи ветвей исходной цепи (рис. 1.1), выполняя алгебраическое сложение частных токов, учитывая их направление:

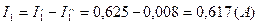
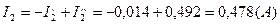
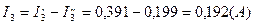
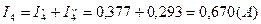
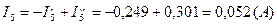
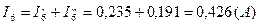
4) Составить баланс мощностей для заданной схемы.

Источники E₁ и Е₂ вырабатывают электрическую энергию, т. к. направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:

E₁I₁+E₂I₂=I²₁(R₁+r₀₁)+I²₂(R₂+r₀₂)+I²₃R₃+I²₄R₄+I²₅R₅+I²₆R₆

Подставляем числовые значения и вычисляем

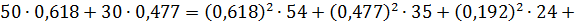
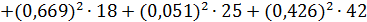
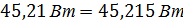
С учетом погрешности расчетов баланс мощностей получился.

5) Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить.

Ток в ветви Метод расчета	I1,A	I2,A	I3,A	I4,A	I5,A	I6,A
метод контурных токов метод наложения	0,618 0,617	0,477 0,478	0,192 0,192	0,669 0,670	0,051 0,052	0,426 0,426

Расчет токов ветвей обоими методами с учетом ошибок вычислений практически одинаков.

6) Определить ток во второй ветви методом эквивалентного генератора.

Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи.

Для решения задачи методом эквивалентного генератора разделим электрическую цепь на две части: потребитель (исследуемая ветвь с со­противлением R₂, в которой требуется определить величину тока) и экви­валентный генератор (оставшаяся часть цепи, которая для потребителя R₂ служит источником электрической энергии, т. е. генератором). Получается схема замещения (рис. 1.4)

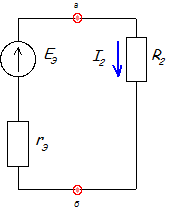
Рис.1.4

На схеме искомый ток I₂ определим по закону Ома для замкнутой цепи:

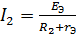
Где Е_Э – ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Е_Э=U_хх.

r_Э – внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассивного двухполюсника относительно исследуемых зажимов.

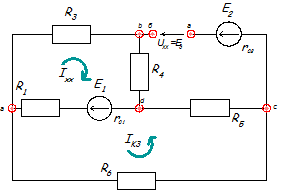
Рис. 1.5

Изображаем схему эквивалентного генератора в режиме холостого хода (рис. 1.5), т. е. при отключенном потребителе R₂ от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода. Определим его величину:

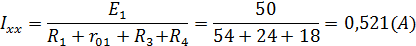
Зная I_хх, величины сопротивлений и ЭДС, в схеме можно определить U_хх как разность потенциалов между клеммами а и б. Для этого потенциал точки б будем считать известным и вычислим потенциал точки а.

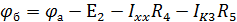
тогда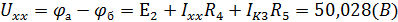

Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать треугольник 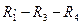в звезду:

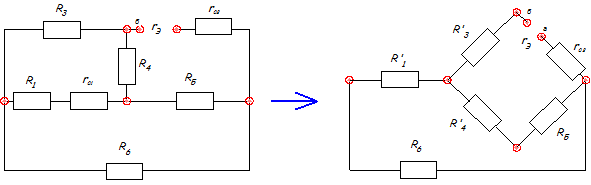
Рис.1.6

Вычисляем эквивалентное сопротивление схемы (рис. 1.6):

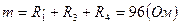
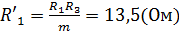
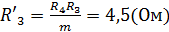
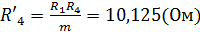
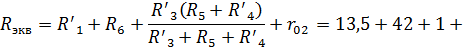
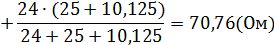
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:

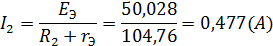
т. е. ток в этой ветви получился таким же, как и в пунктах 2 и 3.

7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

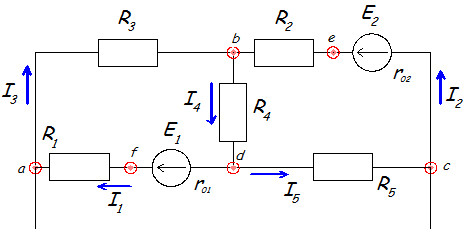
Рис. 1.7

Возьмем контур abcda. Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки a.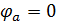

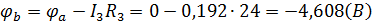
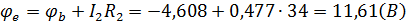
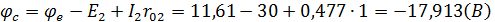
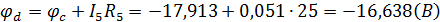
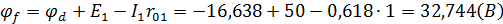
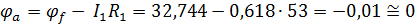
0 - проверочная точка. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака.

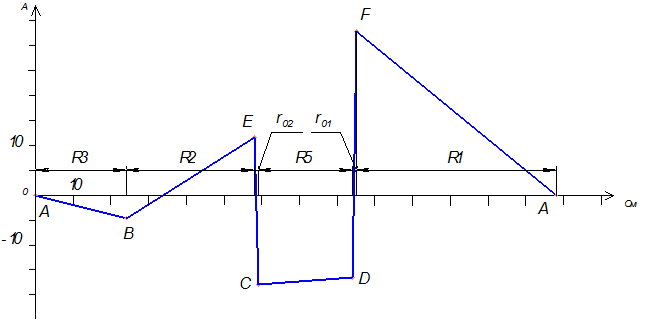
Рис.1.8

2 Анализ электрического состояния линейных электрических цепей однофазного переменного тока

Задание

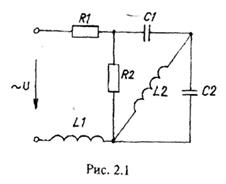
К зажимам электрической цепи, схема замещения которой приведена на рис. 2.1, подключен источник синусоидального напряжения

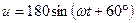В, частотой f = 50 Гц

Параметры элементов схемы замещения:

R₁ = 25Ом, R₂ = 50 Ом, L₁ =79,5 мГн,

L₂ = 127,2 мГн, С₁ = 318 мкФ, С₂ = 79,5 мкФ.

Выполнить следующее:

1) начертить схему замещения электрической цепи, соответствующую варианту, рассчитать реактивные сопротивления элементов цепи;

2) определить действующие значения токов во всех ветвях цепи;

3) записать уравнение мгновенного значения тока источника;

4) составить баланс активных и реактивных мощностей;

5) построить векторную диаграмму токов, совмещенную с топогра­фической векторной диаграммой напряжений.

6) результаты расчетов занесем в соответствующую таблицу.

Дано: R₁ = 25Ом, R₂ = 50 Ом, L₁ = 79,5 мГн,

L₂ = 127,2 мГн, С₁ = 318 мкФ, С₂ = 79,5 мкФ.

Определить:

X_L1, X_L2, X_C1, X_C2, I₁, I₂, I₃, I₄, I₅.

1) Реактивные сопротивления элементов цепи:

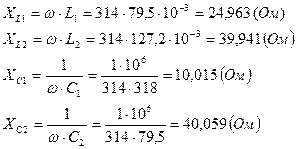
2) Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований.

Представим схему, приведенную на рис. 2.1 в следующем виде:

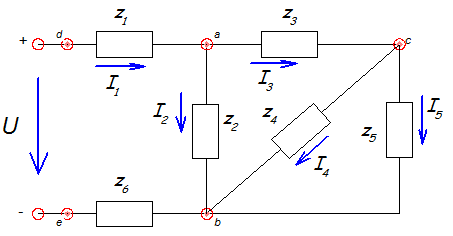
Рис.2.2

Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:

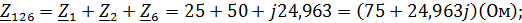
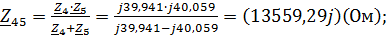
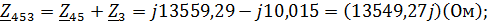
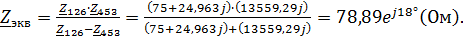
Выразим действующее значение напряжений в комплексной форме:

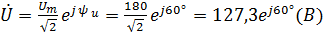
Вычисляем токи ветвей и общий ток цепи:

;

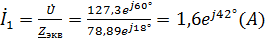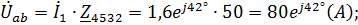
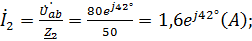
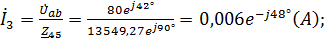
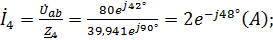
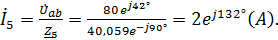
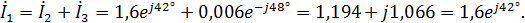
3) Уравнение мгновенно значения тока источника:

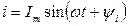
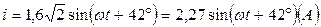
4) Комплексная мощность цепи:

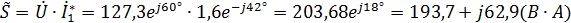, где: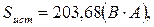

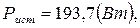
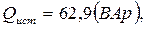(положительный знак определяет индуктивный характер нагрузки в целом).

Активная 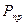и 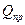реактивная мощность приемников:

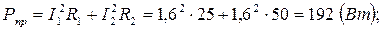
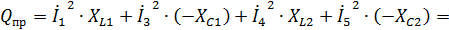
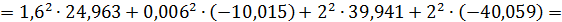
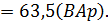
Баланс мощностей выполняется:

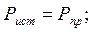
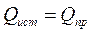
5) Напряжение на элементах схемы замещения цепи:

;

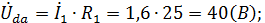
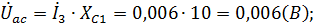
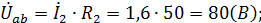
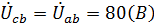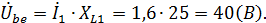
6) Строим топографическую векторную диаграмму на комплексной плоскости.

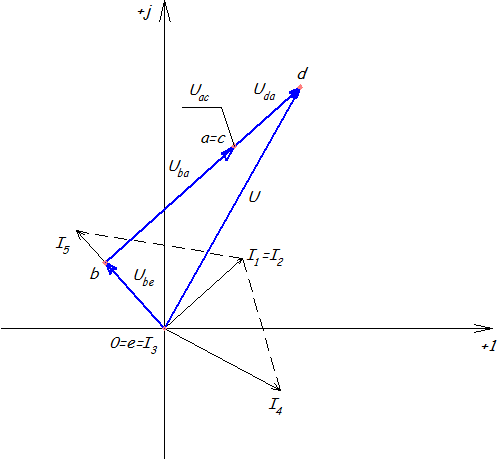
Рис.2.3

7) Результаты расчетов занесем в соответствующие таблицы

Результаты расчетов реактивных сопротивлений

Сопротивления	Действующее значение, Ом
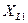	24,963
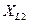	39.941
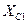	10,015
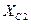	40,059

Результаты расчетов токов

Токи ветвей	Показательная форма, А	Действующее значение, А
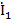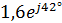		1,6
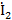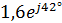		1,6
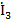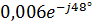		0,006
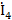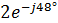
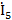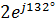