Проверка статистических гипотез
ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Задание 1
Требуется вычислить значения выборочных среднего 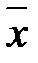 , медианы
, медианы 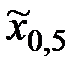 , дисперсии s2, среднего квадратического отклонения s и коэффициента вариации ν ряда значений: 408, 404, 399, 412, 420, 418, 400, 413, 416, 417, 396, 409, 401, 395, 398, 370
, дисперсии s2, среднего квадратического отклонения s и коэффициента вариации ν ряда значений: 408, 404, 399, 412, 420, 418, 400, 413, 416, 417, 396, 409, 401, 395, 398, 370
| i | xi | Предварительные расчёты: 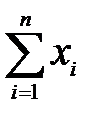 = 6476; = 6476; 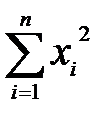 = 2623490. Выборочное среднее значение (2.1): = 2623490. Выборочное среднее значение (2.1): 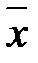 = = 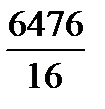 = 404,75. Выборочная медиана (2.3): = 404,75. Выборочная медиана (2.3): 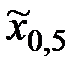 = = 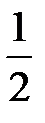 (404+ 408) = 406. Выборочная дисперсия (2.5): s2 = (404+ 408) = 406. Выборочная дисперсия (2.5): s2 = 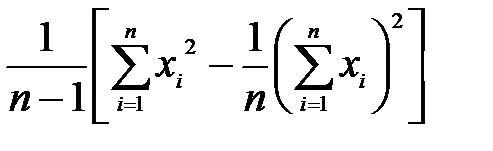 = = 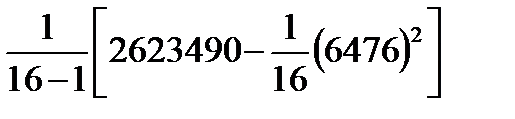 = = 155,267. Смещённая оценка среднего квадратического отклонения (2.6): s = = = 155,267. Смещённая оценка среднего квадратического отклонения (2.6): s = 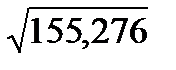 = 12,4606. Несмещённая оценка среднего квадратического отклонения (2.8) и таблица 2.1: s1 = 1,017 · 12,4606=12,6724. Выборочный коэффициент вариации (2.7): ν = = 12,4606. Несмещённая оценка среднего квадратического отклонения (2.8) и таблица 2.1: s1 = 1,017 · 12,4606=12,6724. Выборочный коэффициент вариации (2.7): ν = 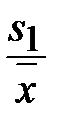 = = 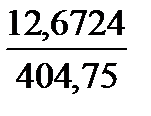 = 0,03131. = 0,03131. |
Выборочная медиана при нечётном объеме выборки n = 2m – 1 равна среднему члену вариационного ряда:
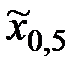 = xm,
= xm,
(2.3)
Выборочная дисперсия
s2 = 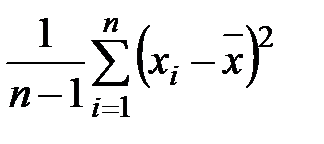 , (2.4)
, (2.4)
или
s2 = 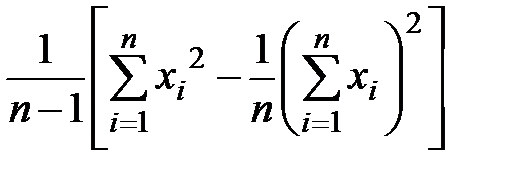 . (2.5)
. (2.5)
Выборочное среднее квадратическое отклонение и выборочный коэффициент вариации
s = 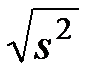 , (2.6)
, (2.6)
ν = 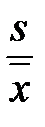 . (2.7)
. (2.7)
Вычисление выборочных моментов третьего и четвёртого порядков при объёме п < 50 нецелесообразно в связи с их большими вероятными отклонениями от генеральных моментов.
Задание 2
Вычислить значения статистик, указанных в примере 2.1, и выборочные значения показателей асимметрии и эксцесса для случайной величины x = lgN. Ряд значений N, Производим логарифмирование и формируем вариационный ряд:
| i | N | xi = lgN | i | N | xi = lgN | i | N | xi = lgN | i | N | xi = lgN |
| 74133,6 | 4,8700 | 5,2085 | 5,4638 | 5,5922 | |||||||
| 83019,5 | 4,9192 | 5,2114 | 5,4654 | 5,5963 | |||||||
| 5,0238 | 5,2311 | 5,4712 | 5,6102 | ||||||||
| 5,0407 | 5,2621 | 5,4721 | 5,6476 | ||||||||
| 5,0447 | 5,3126 | 5,4850 | 5,6479 | ||||||||
| 5,0466 | 5,3321 | 5,4982 | 5,6744 | ||||||||
| 5,0665 | 5,3698 | 5,4991 | 5,8173 | ||||||||
| 5,0818 | 5,3756 | 5,5186 | 5,8652 | ||||||||
| 5,0840 | 5,3821 | 5,5208 | 5,8720 | ||||||||
| 5,1080 | 5,3839 | 5,5221 | 5,8980 | ||||||||
| 5,1100 | 5,3848 | 5,5231 | 5,9054 | ||||||||
| 5,1200 | 5,3927 | 5,5438 | 5,9112 | ||||||||
| 5,1203 | 5,3976 | 5,5471 | 5,9192 | ||||||||
| 5,1255 | 5,4085 | 5,5584 | 5,9302 | ||||||||
| 5,1621 | 5,4095 | 5,5609 | 5,9548 | ||||||||
| 5,1701 | 5,4103 | 5,5613 | 6,0826 | ||||||||
| 5,1761 | 5,4225 | 5,5660 | 6,1684 | ||||||||
| 5,1816 | 5,4336 | 5,5661 | 6,2604 | ||||||||
| 5,1907 | 5,4350 | 5,5799 | 6,2776 | ||||||||
| 5,1966 | 5,4628 | 5,5829 | 6,4587 |
Определяем размах варьирования логарифма:
R = 6,458679992– 4,87001509= 1,5886649.
Размах разбиваем на равные интервалы.
Δx ≈ 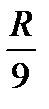 =
= 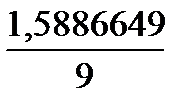 = 0,1765183
= 0,1765183
За длину интервала принимаем Δx = 0,18
Таблица 2.3
| e | Границы интервала | Середина интервала xj | Число наблюдений nj | |
| 4,870 | 5,050 | 4,96 | ||
| 5,050 | 5,230 | 5,14 | ||
| 5,230 | 5,410 | 5,32 | ||
| 5,410 | 5,590 | 5,50 | ||
| 5,590 | 5,770 | 5,68 | ||
| 5,770 | 5,950 | 5,86 | ||
| 5,950 | 6,130 | 6,04 | ||
| 6,130 | 6,310 | 6,22 | ||
| 6,310 | 6,490 | 6,40 |
Предварительные расчёты:
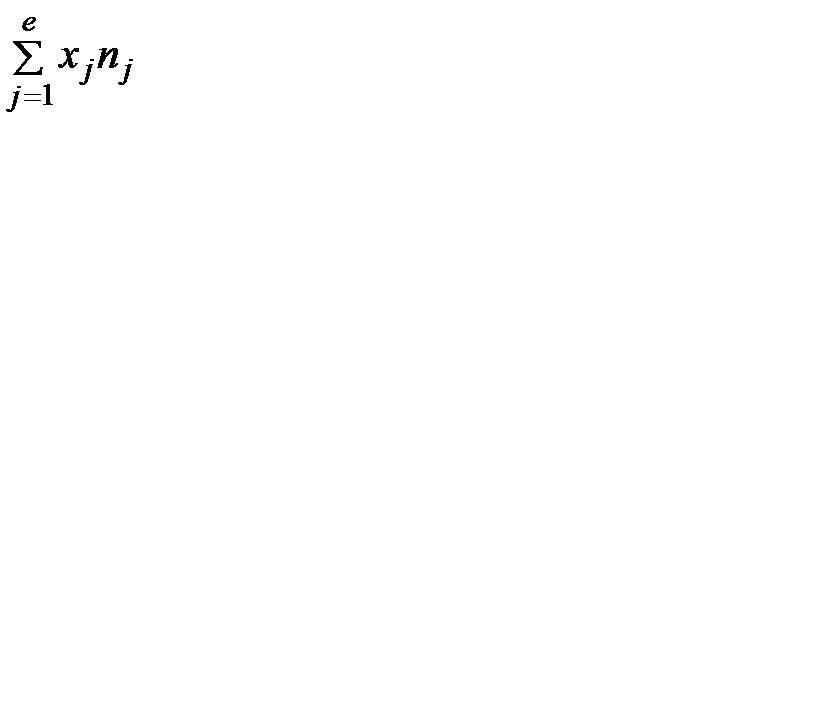 = 436,8;
= 436,8; 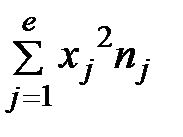 = 2393;
= 2393;
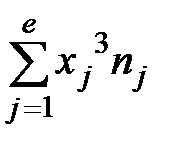 = 13156;
= 13156; 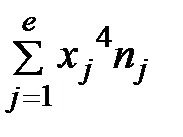 = 72599.
= 72599.
Выборочное среднее значение (2.10):
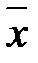 =
= 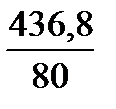 = 5,4595.
= 5,4595.
Выборочная медиана (2.3):
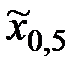 =
= 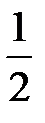 (5,4627+ 5,4638) = 5,4633.
(5,4627+ 5,4638) = 5,4633.
Выборочная дисперсия (2.12):
s2 = 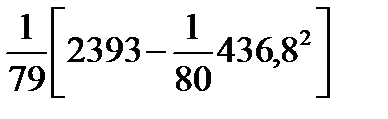 = 0,1050.
= 0,1050.
Выборочное среднее и выборочный коэффициент вариации (2.6) и (2.7):
s = 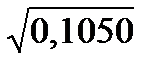 = 0,3240; ν =
= 0,3240; ν = 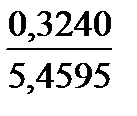 = 0,0593.
= 0,0593.
Для вычисления выборочных показателей ассиметрии и эксцесса по формулам (2.13) определяем оценки начальных моментов первых четырёх порядков:
h1 = 5,4560; h2 = 29,91;
h3 = 164,45; h4 = 907,49.
и по формулам (2.14) – оценки центральных моментов третьего и четвёртого порядка
m3 = 0,0227;
m4 = 0,0347.
Выборочные показатели ассиметрии и эксцесса
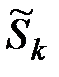 =
= 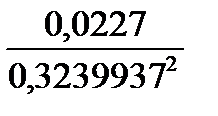 = 0,6680722;
= 0,6680722; 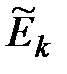 =
= 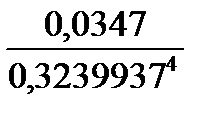 –3 = 0,1516.
–3 = 0,1516.
Задание 3
По данным примера 2.2 произвести оценку математического ожидания и среднего квадратического отклонения при условии, что испытания прекращали при достижении базы Nб = 0,5·106 циклов, т.е. xб = lg Nб = 5,6990.
По таблице 2.2 находим m = 66 и по формуле (2.20) вычисляем:
W = 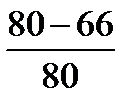 = 0,175.
= 0,175.
По формуле (2.21)
y = 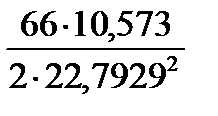 = 0,6716.
= 0,6716.
По таблице 2.5 для W = 0,175 и y = 0,6716 путём линейной интерполяции находи u = –0,984.
По таблице 2.6 находим
φ1(–0,984) = 1,4456
По формуле (2.23) производим оценку среднего квадратического отклонения s = 0,2675
По формуле (2.22) производим оценку математического ожидания
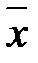 =
= 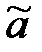 = 5,69897– 0,984 · 0,2675 = 5,4357.
= 5,69897– 0,984 · 0,2675 = 5,4357.
Задание 4
По результатам примера 2.1 определить 90 %-ные доверительные интервалы для генерального среднего значения, если 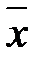 = 404,75; s = 12,4606.
= 404,75; s = 12,4606.
По таблице 2.6 для k = 16 – 1 = 15 и α = 0,1 находим t0,1 = 1,7535.
На основании формулы (2.26)
404,75 – 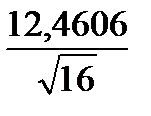 1,7535 < a < 404,75 +
1,7535 < a < 404,75 + 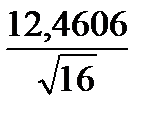 1,7535;
1,7535;
399,2876 < a < 410,2124
В случае цензурированной выборки доверительный интервал для доверительной вероятности Р = 1 – α приближённо определяют из выражения
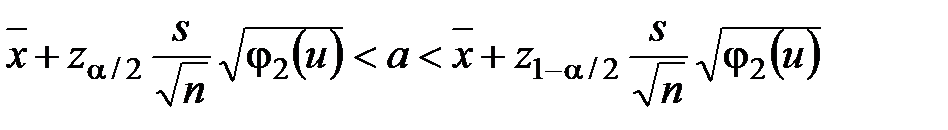 (2.27)
(2.27)
Задание 5
По результатам таблицы 2.2 определить 90 %-ные доверительные интервалы для генерального среднего значения, если 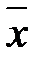 = 5,4357; s = 0,2675; u = –0,9842 (см. пример 2.3).
= 5,4357; s = 0,2675; u = –0,9842 (см. пример 2.3).
Для α = 0,1 по таблице 2.7 находим
z0,05 = -1,282;
z0,95 = 1,282.
По найденному в примере 2.3 u = –0,9842 по таблице 2.6
φ2(0,9842) = 1,054.
На основании (2.27)
5,4357– 1,282 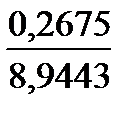
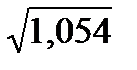 < a < 5,4357+ 1,282
< a < 5,4357+ 1,282 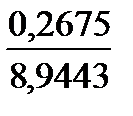
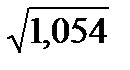
5,3963< a < 5,4750
Доверительный интервал для генеральной дисперсии σ2 с доверительной вероятностью Р = 1 – α
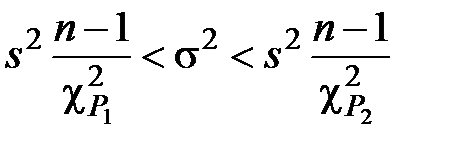 . (2.28)
. (2.28)
Обычно принимают Р1 = α/2 и Р2 = 1 – Р1 = 1 – α/2.
Границы доверительных интервалов для генерального среднего квадратического отклонения σ находят путём извлечения квадратного корня из значений доверительных границ для генеральной дисперсии.
Задание 6
По результатам примера 2.1 определить 90 %-ные доверительные интервалы для генеральных дисперсии и среднего квадратического отклонения, если s2 = 155,2667 .
По таблице 2.9 для k = n – 1 = 15 находим
χ0,052 = 25;
χ0,952 = 7,26.
На основании (2.28)
155,2667 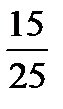 < σ2 < 155,2667
< σ2 < 155,2667  ;
;
93,16< σ2 < 320,7989;
9,651943< σ < 17,91086.
В случае цензурированной выборки доверительный интервал для генерального среднего квадратического отклонения приближённо определяют из выражения
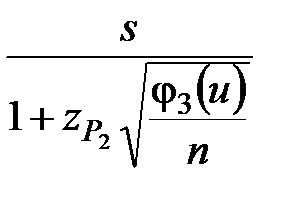 < σ <
< σ < 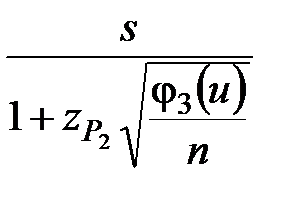 . (2.29)
. (2.29)
Задание 7
В условиях примера 2.2 определить 90 %-ные доверительные интервалы для генерального среднего квадратического отклонения значения логарифма, если s = 0,2675 и u = –0,9842
Для α = 0,1 по таблице 2.7 находим
z0,05 = -1,282
z0,95 = 1,282
φ3(u) = φ3(–0,9842) = 0,6707
На основании (2.35)
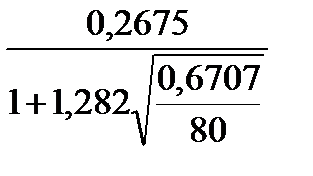 < σ <
< σ < 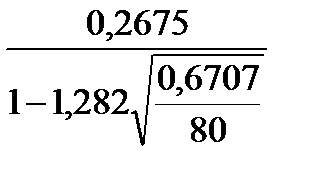 ;
;
0,2394< σ < 0,3031
Задание 8
Определить необходимый объём испытаний образцов с целью оценки среднего значения, если α = 0,05 и Δa = 0,07. Данные о коэффициенте вариации при аналогичных испытаниях отсутствуют.
Задаёмся коэффициентом вариации γ = 0,03. По таблице 2.7 для p = 1-0,05/2=0,975 находим z0,975 = 1,96 и по формуле (2.31) определяем
n = 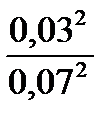 1,962 ≈ 0, 71
1,962 ≈ 0, 71
Принимаем
n = 1
Если цель планируемых испытаний – оценка среднего квадратического отклонения характеристики, то объём выборки определяют методом подбора по формуле
(1 + Δσ)2 = 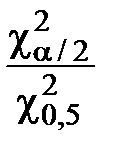 , (2.35)
, (2.35)
где Δσ – максимальная относительная ошибка (допуск) при оценке среднего квадратического отклонения случайной величины при нормальном законе распределения; χ2α/2 и χ20,5 – квантили уровня Р = α/2 и Р = 0,5 статистики χ2 (таблица 2.9).
Значение ошибки Δσ следует выбирать в зависимости от требований к точности оценки среднего квадратического отклонения характеристики. При низкой точности принимают Δσ = 0,4 … 0,5, при средней точности Δσ = 0,25 … 0,35 и при высокой точности Δσ = 0,1 … 0,2.
При n ≥ 15 для определения объёма выборки вместо (2.35) можно воспоьзоваться приближённой формулой
n = 1,5 + 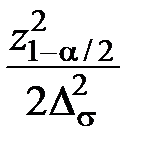 , (2.36)
, (2.36)
Задание 9
Определить минимально необходимый объём испытаний с целью оценки среднего квадратического отклонения, если α = 0,05 и Δσ = 0,6.
Подсчитываем левую часть уравнения (2.36)
(1 + Δσ)2 = (1 + 0,6)2 = 2,56
По таблице 2.10 для различных k = n – 1 вычисляем отношения χ20,05 и χ20,5, выбираем такое значение k = n – 1, при котором отношение указанных величин будет меньше или равняться значения левой части уравнения (2.35).
Для k = 1
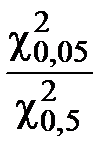 =
= 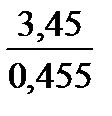 = 7,648352
= 7,648352
Для k = 3
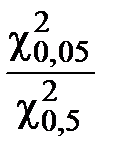 =
= 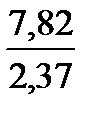 = 3,299578
= 3,299578
Для k = 4
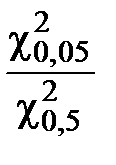 =
= 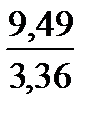 = 2,824405
= 2,824405
Для k = 5
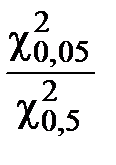 =
= 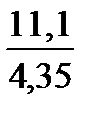 = 2,551724
= 2,551724
Окончательно принимаем n = k + 1 = 6
При использовании формулы (2.36) получаем
n = 1,5 + 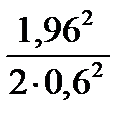 = 6, 84
= 6, 84
Если в результате испытаний планируется одновременная оценка и среднего значения, и среднего квадратического отклонения контролируемой характеристики с заданной точностью и надёжностью, то объём испытаний определяют как наибольшее из двух значений n, найденных по формулам (2.31) – (2.33) и (2.35) – (2.36).
Для этой цели могут быть также использованы таблицы 2.10 и 2.11.
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Задание 1
По результатам примера 2.1 проверить нулевую гипотезу о принадлежности последнего образца вариационного ряда той же генеральной совокупности, как и остальные образцы.
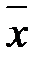 = 404,75
= 404,75
s = 12,4606
un = 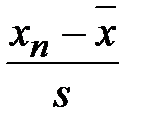 =
= 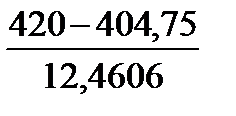 = 1,223857.
= 1,223857.
un = 1,223857< uα=2,44
Заключение: нулевая гипотеза не отклоняется, т.е. результат x20 = 420 не является следствием грубой ошибки эксперимента.
Задание 2
По результатам испытания 18 образцов произведена оценка дисперсии s2 = 126,9. Проверить нулевую гипотезу, заключающуюся в том, что выборка взята из генеральной совокупности с дисперсией σ20 = 100 против альтернативной σ2 > σ20.
Вычисляем левую часть неравенства (3.3):
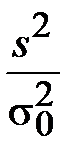 =
= 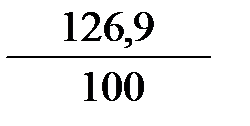 =1,269
=1,269
Задаёмсяα = 0,05 и по таблице 2.10 находим для k = n – 1 = 17
χ20,05 = 27,6
Вычисляем правую часть соотношения (3.3)
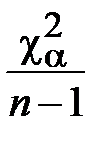 =
= 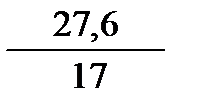 = 1,269
= 1,269
Заключение: неравенство (3.3) не выполняется, следовательно, применяют альтернативную гипотизу.
Задание 3
Определить минимальный объём выборки для проверки нулевой гипотезы о равенстве дисперсий с помощью двустороннего критерия (3.5), если α = 0,05; β = 0,07 и Δσ = 0,3
По таблице 2.8 находим z1–β = z0,9 = 1,282; z1–α/2 = z0,975 = 1,96.
На основании формулы (3.7) определяем
n = 1,5 + 0,5 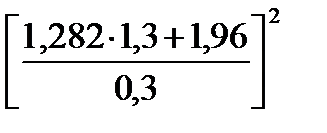 ≈ 75
≈ 75
Критерий равенства дисперсий двух генеральных совокупностей. Пусть по результатам испытаний двух независимых выборок объёмом n1 и n2 из нормально распределённых совокупностей подсчитаны оценки дисперсий, причём s21 > s22. Требуется проверить нулевую гипотезу о том, что указанные выборки принадлежат генеральным совокупностям с равными дисперсиями, т.е. σ21 = σ22 = σ2 при альтернативной гипотезе σ21 ≠ σ22. С этой целью используют двусторонний F-критерий (критерий Фишера), для чего находят статистику
F = 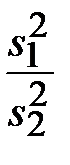 при s21 > s22. (3.8)
при s21 > s22. (3.8)
И сопоставляют с критическим значением F1–α/2, представленным в 3.3
Если
F = 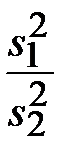 ≤ F1–α/2, (3.9)
≤ F1–α/2, (3.9)
то гипотезу о равенстве дисперсий двух генеральных совокупностей, из которых взяты выборки, т.е. σ21 = σ22 = σ2, не отклоняют.
В случае невыполнения неравенства (3.9) нулевую гипотезу отвергают.
При альтернативной гипотезе σ21 > σ22 используют односторонний критерий
F = 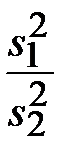 ≤ F1–α, (3.10)
≤ F1–α, (3.10)
если неравенство выполняется, то нулевую гипотезу не отвергают. В противном случае принимают σ21 > σ22.
В случае подтверждения нулевой гипотезы σ21 = σ22 = σ2 по двум выборочным дисперсиям производят новую оценку генеральной дисперсии σ2:
s2 = 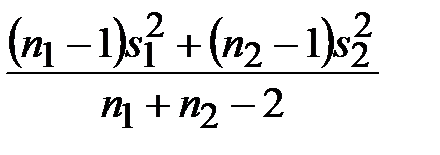
Задание 4
В результате испытаний двух партий 30 образцов и 20 образцов соответственно найдены выборочные средние значения и дисперсии предела прочности сплава. α = 0,1.
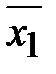 = 47; s12 = 88.
= 47; s12 = 88.
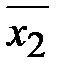 = 45; s22 = 105
= 45; s22 = 105
Требуется проверить гипотезу о равенстве генеральных дисперсий предела прочности материала при альтернативной гипотезе σ21 ≠ σ22.
В соответствии с соотношением (3.10)
F = 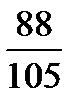 = 0,8381.
= 0,8381.
Для принятого уровня значимости α = 0,1; k1 = n1 – 1 = 27 и k2 = n2 – 1 = 29 по таблице 3.3 находим
F1–α/2 = F0,95 = 1,8751 и сопоставляем с вычисленным значением
F = 0,8381< F0,95 = 1,8751
Заключение: дисперсии однородны.
