ЛЕКЦИЯ № 30. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Вопрос 1. Линейные дифференциальные уравнения старших порядков.

Вопрос 30.2. Системы линейных дифференциальных уравнений первого порядка.

Список литературы ……………………………………………………….157

ЛЕКЦИЯ № 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

Вопрос 1.1. Первообразная и неопределенный интеграл.

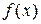Определение 1.1.1. Функция называется первообразной для функции на интервале , если для всех x из интервала .

Конец определения.

Очевидно, что если первообразная для функции 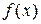, то и тоже первообразная для 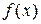. Справедливо и обратное утверждение.

Теорема 1.1.1. Если и две первообразные для функции 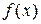, то они отличаются на константу.

Доказательство. Так как выполняются равенства , , то, вычитая из первого равенства второе, получим

.

Из равенства нулю производной, заключаем, что разность функций принимает постоянное значение, откуда и следует доказываемое утверждение

.

Конец доказательства.

Определение 1.1.2. Неопределенным интегралом от функции 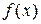на интервале называется множество всех ее первообразных, которое обозначается символом

.

Конец определения.

Свойства неопределенного интеграла:

1) ,

2) .

Доказательство. Доказательство следует из равенства:

.

Конец доказательства.

3) .

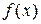Доказательство. Пусть и есть первообразные для функций и соответственно. Тогда сумма есть первообразная для функции , и, следовательно, справедливо равенство

.

Поскольку равенство неопределенных интегралов понимается с точностью до константы, то отсюда следует доказываемое соотношение.

Конец доказательства.

4) .

Доказывается аналогично 3-ему свойству.

5) .

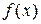Доказательство. Пусть есть первообразная для функции , тогда функция есть первообразная для функции , отсюда получаем

,

где учтено, что . Отсюда, по тем же причинам, что и в доказательстве свойства 3 следует справедливость свойства 4.

Конец доказательства.

6) .

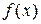Доказательство. Пусть есть первообразная для функции , тогда функция есть первообразная для функции

.

Отсюда получаем

.

Конец доказательства.

Вопрос 1.2. Таблица интегралов.

Таблица интегралов играет в высшей математике такую же важную роль, что и таблица производных. Она состоит из наиболее часто встречающихся интегралов от элементарных функций. Эти интегралы получаются с помощью таблицы производных из определения неопределенного интеграла.

.

1. .

2. .

3. .

.

4. .

5. .

6.

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14.

15. .

Докажем например формулу 2. Вычислим производную от . Если , то , тогда . Если , то , тогда . Поэтому .

Замечание 1.1. Некоторые интегралы могут быть выражены через другие функции.

Например:

,

,

,

где ‑ аркгиперболический синус (функция ‑ обратная к гиперболическому синусу) и ‑ аркгиперболический тангенс (функция ‑ обратная к гиперболическому тангенсу)