Система совместных уравнений

При использовании отдельных уравнений регрессии,например для экономических расчетов,предположим,что аргументы (факторы) можно изменить независимо друг от друга.Однако,это предположение является очень грубым.Практическое изменение одной переменной не может происходить при неизменности других. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинное влияние отдельных признаков на вариацию результирующих переменных .В экономическом исследовании важна проблема описания структуры связи между переменными. Наибольшее распространение в эконометрике получила система взаимозависимых уравнений.

Y1=b12*y2+b13*y3+…+b1n*yn+a11*x1+a12*x2+…+a1m*xm

Y2=b21*y1+b23*y3+…+b2n*yn+a21*x1+a22*x2+…+a2m*xm

Y3=bn1*y1+bn2*y2+…+bnn-1*yn-1+an1*x1+an2*x2+…+anm*xm

Система взаимозависимых уравнений получила название системы совместных,одновременных уравнений.То есть в системе одни и те же переменные «у» одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других.Каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно и для нахождения его параметров традиционный МНК не применим.

Система совместных одновременных уравнений обычно содержит эндо- и –экзогенные переменные. Эндогенные ( зависимые «у») переменные- зависимые переменные ,число которых равно числу уравнений в системе и которые обычно обозначаются через «у».

Экзогенные переменные- предопределенные переменные ,влияющие на эндогенные, но независящие от них. Обозначаются через «х».Система в правой части содержит при эндогенных переменных .коэф «а», который называется структурным коэф. модели.

Проблема идентификации.

При переходе от приведенной формы модели к структурной мы сталкиваемся с проблемой идентификации. Идентификация-единственность соответствий между приведенной и структурной формами модели. Чтобы получить единственное возможное решение для структурной модели необходимо предположить,что некоторые из структурных коэф. модели из-за слабого взаимодействия признаков с эндогенной переменной (у) равны нулю,тем самым уменьшить число структурных коэф.модели.

На структур. коэф. могут накладываться ограничения вида bik+ag=0

C позиции идентификации структуру модели можно подразделить на три вида:

1)идентифицируемая

2)неидентифицируемая

3)сверхидентифицируемая

Модель идентиф. если все структур.коэф. определяются однозначно,единственным образом по коэф.приведенной формы модели,т.е. если число параметров структ.модели равно числу парам.привед.формы модели.

Модель неидентиф. Если число привед.коэф. меньше числа стуктур.коэф. и в результате структур.коэф. не могут быть оценены через коэф.привед. формы.

Модель сверхидентифицир.,если число привед.коэф.больше,чем число структур.коэф.В этом случае на основе коэф.привед.формы можно получить два или более значений одного структурного коэф.

Структурная модель представляет собой систему совместных уравнений,в каждом из которых необходима иденитификация.Если обозначить число эндоген.перемен. в уравнении через «Н»,а число экзогенных «D»,котор. Содержится в системе,но не входят в данное уравнение,то в условиях идентифицируемости модели может быть записано след.правило :

D+1=H (идентиф.)

D+1<H(неидентиф.)

D+1>H(сверхидентиф.)

Это правило необходимое условие ,но не достаточное.Более точно условие идентиф. Определяется, если накладывать ограничения на коэф.матриц параметров структур.модели.

Уравнение идентифиц.,если при отсутствии в нем переменных можно из коэф. других уравнений получить матрицу,определитель которой не равен нулю,а ранг матрицы не меньше чем число эндоген.перемен. в системе без одного.

37.Система совместных одновременных уравнений обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные – зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через y. Экзогенные уравнения – предопределённые переменные, влияющие на эндогенные переменные, но не зависящие от них, обозначаются через x.
Структурная форма модели в правой части содержит при эндогенных переменных коэфициенты 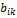и экзогенных переменных – коэфициенты 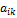, которые называются структурными коэф модели.
Все переменные в модели выражены в отклонениях от сред. уровня, то есть под X подразумевается x- 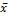, а под y => y- 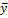. Для определения коэф модели структурная форма модели преобразуется в приведенную форму модели. Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

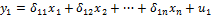
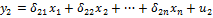
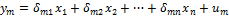
где 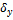– коэфициенты приведенной формы модели.

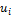- остаточная величина для приведенной формы.

По своему виду приведенная форма модели не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК можно оценить 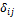, а затем оценить эндогенные переменные через экзогенные. Коэф приведенной формы модели представляют собой нелинейные функции коэф-тов структурной формы модели.

38. Коэфициенты структурной модели могут быть оценены разными способами взависимости от вида одновренных уравнений.
Методы оценивания коэф-тов структурной модели:
1) Косвенный МНК(КМНК)

2)Двухшаговый МНК(ДМНК)

3)Трехшаговый МНК(ТМНК)

4)МНП с полной информацией

5)МНП при огранич. информации

Применение КМНК:

КМНК применяется в случае точной идентификации структурной модели.

Процедуры примения КМНК:
1. Структурн. модель преобраз. в привед. форму модели.

2. Для каждого уравнения привед. форма модели обычным МНК оцениваются привед. коэф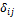

3. Коэфициенты приведенной формы модели трансформируются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не исп, так как не дает однозначных оценок для параметров структурной модели. В этом случае могут исп. разные методы оценивания, среди которых наиболее распространен ДМНК.
Основная идея ДМНК-на основе приведенной модели получить получить для сверхидентиф. уравнения теор. значения эндогенных переменных, содерж. в правой части ур-ния. Далее подставив в найденные значения вместо факт.значений применяется обычный МНК и структурн. форма сверхидент. ур-ния.
1 шаг: при опред. привед. формы модели и нахождении на ее основе оценок теор. значений эндогенной переменой

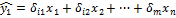
2 шаг: Применительно к структурному сверхидентифицируемому уравнению при определении структурных коэфициентов модели по данным теоритических значений эндогенных переменных.