Алгоритм 1.4. Расчет средних групповых значений результативного признака

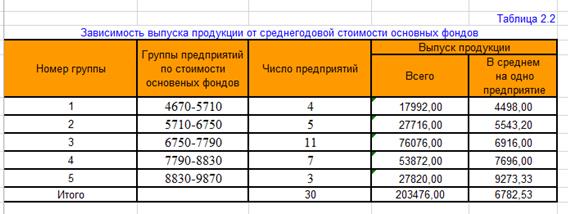
В таблице 2.2 приведены формулы для расчета средних групповых значений результативного признака Выпуск продукции.

1. В ячейке (Е41), выделенной для среднего значения результативного признакаВыпуск продукции первойгруппы, перед формулой поставить знак равенства «=»;

Enter;

3. Выполнить действия 1–2 поочередно для всех групп;

4. В ячейках (C46, D46иE46), выделенных для расчета итоговых сумм:

Перед формулой поставить знак равенства «=»;

Enter.

Результаты работы алгоритмов 1.3 и 1.4 для демонстрационного примера приведены в табл. 2.2.

Задача 2. Оценка тесноты связи изучаемых признаков на основе эмпирического корреляционного отношения

Задача решается в два этапа:

1. Расчет внутригрупповых дисперсий результативного признака.

2. Расчет эмпирического корреляционного отношения.

Алгоритм 2.1. Расчет внутригрупповых дисперсий результативного признака

1. В ячейке, выделенной для внутригрупповых дисперсий первойгруппы (D52), перед формулой поставить знак равенства «=»; (В качествеаргумента функции ДИСПР() указан диапазон ячеек из табл. 2.1 со значениями y_i первойгруппы – визуально легко определяется по цвету заливки диапазона);

2. Enter;

3. Выполнить действия 1–3 поочередно для всех групп, используя цветовые заливки диапазонов.

4. Для расчета итоговой суммы в табл. 2.3 (в ячейке C57) перед формулой необходимо поставить знак равенства «=»;

Enter.

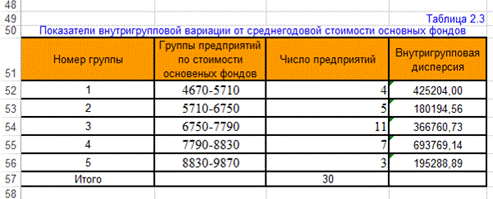
Результат работы алгоритма 2.1 для демонстрационного примера (вариант №102) представлен в табл.2.3.

Алгоритм 2.2. Расчет эмпирического корреляционного отношения

1. В ячейке, выделенной для общей дисперсии (А63), перед формулой поставить знак равенства «=»;

Enter;

3. В ячейке, выделенной для средней из внутригрупповых дисперсий (В63), перед формулой поставить знак равенства «=»;

Enter;

►Примечание. В случае если при выполнении вычисления в ячейке В63 выдается сообщение "Ошибка в формуле", то разделительный знак «,» между аргументами функции СУМПРОИЗВ(Д1,Д2) необходимо заменить на знак «;».

5. В ячейке, выделенной для значения межгрупповой (факторной) дисперсии (С63), перед формулой поставить знак равенства «=»;

Enter;

7. В ячейке, выделенной для эмпирического корреляционного отношения (D63), перед формулой поставить знак равенства «=»;

Enter.

Результат работы алгоритма 2.2 для демонстрационного примера (вариант №102) представлен в табл.2.4.

Задание 2

Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия надстройки Пакет анализа

Алгоритм выполнения Задания 2