Физическая реализация звена.

ЛЕКЦИЯ 5.

Дифференцирующее звено

Передаточная функция.

Передаточная функция дифференцирующего звена имеет вид:

W(s) = T·s где T – постоянная времени (время дифференцирования).

Математическое описание звена.

Дифференцирующее звено описывается уравнением, в котором встречается производная от входного сигнала:

у = T·dх(t)/dt

Это не дифференциальное уравнение, поскольку входной сигнал х(t) и его производные полагаются заранее известными.

Физическая реализация звена.

Сразу отметим, что идеальное дифференцирующее звено физически нереализуемо. Вообще, любая передаточная функция с порядком числителя большим порядка знаменателя является физически нереализуемой. Укажем, какие факторы могут воспрепятствовать физической реализуемости:

§ нарушение причинности – выходной сигнал появляется раньше входного;

§ нереализуемая частотная характеристика, например, не стремящаяся к нулю при бесконечно больших частотах;

§ появление на выходе бесконечных значений сигналов при подаче физически реализуемых сигналов.

Строго говоря, физически нереализуемой является и ПФ с порядком числителя равным порядку знаменателя. Как мы видели ранее, даже идеальный усилитель не может быть физически реализован, не говоря уже об идеальном дифференцирующем звене, так как в обоих случаях АЧХ не стремятся к нулю при росте частоты.

Поскольку идеальное дифференцирующее звено физически нереализуемо, при этом сама операция дифференцирования часто встречается при описании процессов разной природы, то на практике часто используют "нетиповое" реальное дифференцирующее звено.Реальное дифференцирующее звено является соединением двух типовых звеньев - идеального дифференцирующего и инерционного, которые вместе приближённо описывающих операцию дифференцирования. Передаточная функция реального дифференцирующего звена имеет вид:

W(s) = T₁s/(T₂s + 1), где T₁ – постоянная времени дифференцирующей составляющей (время дифференцирования), а T₂ – постоянная времени апериодической составляющей. При малых значениях T₂, т.е. когда инерционность апериодического звена мала, составляющей T₂s в знаменателе передаточной функции можно пренебречь, тогда мы получим приближенную передаточную функцию идеального дифференцирующего звена:

W(s) = T₁s/(T₂s + 1) ≈ T₁s.

Такое звено хорошо работает при низких частотах. Максимальная частота, при которой реальное дифференцирующее звено еще работает "почти как идеальное" равна:

ω = 1/T₂.

Примерами дифференцирующего звена являются дифференцирующая цепочка, дифференцирующий трансформатор, операционный усилитель в режиме дифференцирования.

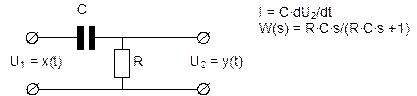
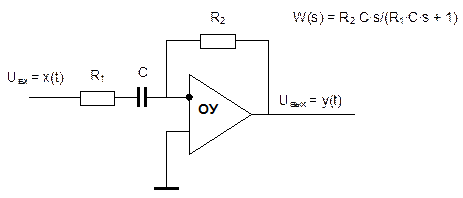
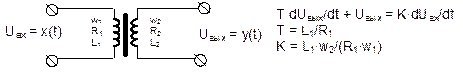
Переходная функция.

h(t) = L^-1[W(s)/s] = L^-1[T] = T·δ(t)

Таким образом, реакция дифференцирующего звена на ступенчатую функцию – это короткий импульс.

Весовая функция.

w(t) = L^-1[W(s)] = L^-1[T·s] = T·dδ(t)/dt

Переходную и весовую функцию дифференцирующего звена трудно изобразить графически, и тем более сложно представить, каков отклик (реакция) этого звена на входное воздействие. Поэтому рассмотрим отклик дифференцирующего звена на линейное (нарастающее) входное воздействие:

х(t) = t Х(s) = 1/s².

у(t) = L^-1[W(s)·Х(s)] = L^-1[T·s/s²] = L^-1[T/s] = T·1(t).

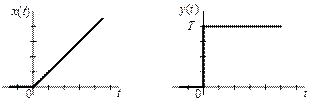
Другими словами, если на вход дифференцирующего звена подать линейно нарастающий сигнал, то в момент подачи сигнала на выходе мы будем иметь скачок выходного сигнала с 0 до T.

Частотные характеристики.

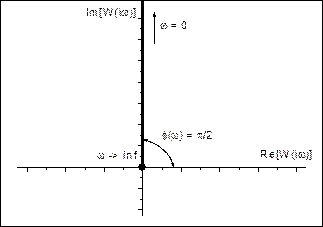
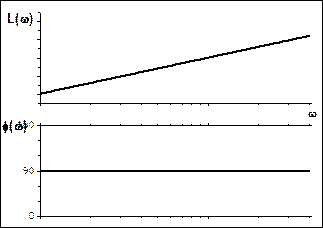
Рис. 5.1. АФЧХ, ЛАХ и ЛФХ дифференцирующего звена.

W(jω) = T·j·ω = 0 + Tω·j

A(ω) = Tω

φ(ω) = arctg(Tω/0) arctg(∞) = π/2

L(ω) = 20lg[A(ω)] = 20lg(Tω).

Как видим, частотные характеристики дифференцирующего звена обратны частотным характеристикам интегрирующего звена.

Форсирующее звено I-ого порядка

Передаточная функция.

Передаточная функция форсирующего звена I-ого порядка имеет вид:

W(s) = K·(Ts + 1) где K – коэффициент усиления; T – постоянная времени.