Общий способ вычисления моментов инерции сложных сечений.
При проверке прочности частей конструкций нам приходится встречаться с сечениями довольно сложной формы, для которых нельзя вычислить момент инерции таким простым путем, каким мы пользовались для прямоугольника и круга.
Таким сечением может быть, например, тавр (Рис.5 а) кольцевое сечение трубы, работающей на изгиб (авиационные конструкции) (Рис.5, б), кольцевое сечение шейки вала или еще более сложные сечения. Все эти сечения можно разбить на простейшие, как-то: прямоугольники, треугольники, круги и т.д. Можно показать, что момент инерции такой сложной фигуры является суммой моментов инерции частей, на которые мы ее разбиваем.
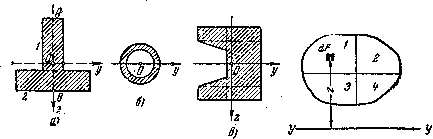
Рис.5. Сечения типа тавр — а) и кольцо б)
Известно, что момент инерции любой фигуры относительно оси у—у равен:
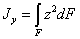
где z—расстояние элементарных площадок 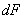 до оси у—у.
до оси у—у.
Разобьем взятую площадь на четыре части: 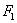 ,
, 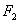 ,
, 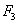 и
и 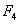 . Теперь при вычислении момента инерции можно сгруппировать слагаемые в подинтегральной функции так, чтобы отдельно произвести суммирование для каждой из выделенных четырех площадей, а затем эти суммы сложить. Величина интеграла от этого не изменится.
. Теперь при вычислении момента инерции можно сгруппировать слагаемые в подинтегральной функции так, чтобы отдельно произвести суммирование для каждой из выделенных четырех площадей, а затем эти суммы сложить. Величина интеграла от этого не изменится.
Наш интеграл разобьется на четыре интеграла, каждый из которых будет охватывать одну из площадей 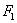 ,
, 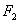 ,
, 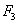 и
и 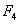 :
:
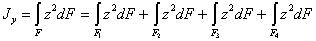
Каждый из этих интегралов представляет собой момент инерции соответствующей части площади относительно оси у — у; поэтому
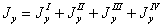
где 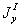 — момент инерции относительно оси у — у площади
— момент инерции относительно оси у — у площади 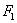 ,
, 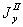 — то же для площади
— то же для площади 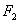 и т. д.
и т. д.
Полученный результат можно формулировать так: момент инерции сложной фигуры равен сумме моментов инерции составных ее частей. Таким образом, нам необходимо уметь вычислять момент инерции любой фигуры относительно любой оси, лежащей в ее плоскости.
Решение этой задачи и составляет содержание настоящей и последующих двух собеседований.
Лекция № 17. Моменты инерции относительно параллельных осей.
Задачу — получить наиболее простые формулы для вычисления момента инерции любой фигуры относительно любой оси — будем решать в несколько приемов. Если взять серию осей, параллельных друг другу, то оказывается, что можно легко вычислить моменты инерции фигуры относительно любой из этих осей, зная ее момент инерции относительно оси, проходящей через центр тяжести фигуры параллельно выбранным осям.

Рис.1. Расчетная модель определения моментов инерции для параллельных осей.
Оси, проходящие через центр тяжести, мы будем называть центральными осями. Возьмем (Рис.1) произвольную фигуру. Проведем центральную ось Оу, момент инерции относительно этой оси назовем 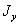 . Проведем в плоскости фигуры ось
. Проведем в плоскости фигуры ось 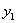 параллельно оси у на расстоянии
параллельно оси у на расстоянии 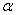 от нее. Найдем зависимость между
от нее. Найдем зависимость между 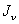 и
и 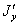 — моментом инерции относительно оси
— моментом инерции относительно оси 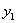 . Для этого напишем выражения для
. Для этого напишем выражения для 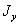 и
и 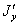 . Разобьем площадь фигуры на площадки
. Разобьем площадь фигуры на площадки 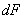 ; расстояния каждой такой площадки до осей у и
; расстояния каждой такой площадки до осей у и 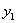 назовем
назовем 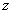 и
и 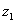 . Тогда
. Тогда
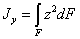 и
и 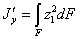
Из рис.1 имеем:
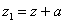
Первый из этих трех интегралов — момент инерции относительно центральной оси Оу. Второй — статический момент относительно той же оси; он равен нулю, так как ось у проходит через центр тяжести фигуры. Наконец, третий интеграл равен площади фигуры F. Таким образом,
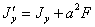 | (1) |
т. е. момент инерции относительно любой оси равен моменту инерции относительно центральной оси, проведенной параллельно у данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Значит, наша задача теперь свелась к вычислению только центральных моментов инерции; если мы их будем знать, то сможем вычислить момент инерции относительно любой другой оси. Из формулы (1) следует, что центральный момент инерции является наименьшим среди моментов инерции относительно параллельных осей и для него мы получаем:
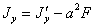
Найдем также центробежный момент инерции 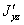 относительно осей
относительно осей 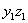 , параллельных центральным, если известен
, параллельных центральным, если известен 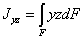 (Рис.1). Так как по определению
(Рис.1). Так как по определению
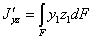
где: 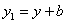 ,
, 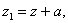 то отсюда следует
то отсюда следует
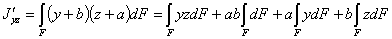
Так как два последних интеграла представляют собой статические моменты площади относительно центральных осей Оу и Oz то они обращаются в нуль и, следовательно:
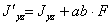 | (2) |
Центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно этих центральных осей плюс произведение из площади фигуры, на координаты ее центра тяжести относительно новых осей.
Зависимость между моментами инерции при повороте осей.
Центральных осей можно провести сколько угодно. Является вопрос, нельзя ли выразить момент инерции относительно любой центральной оси в зависимости от момента инерции относительно одной или двух определенных осей. Для этого посмотрим, как будут меняться моменты инерции относительно двух взаимно перпендикулярных осей при повороте их на угол 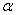 .
.
Возьмем какую-либо фигуру и проведем через ее центр тяжести О две взаимно перпендикулярные оси Оу и Oz (Рис.2).
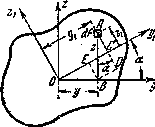
Рис.2. Расчетная модель для определения моментов инерции для повернутых осей.
Пусть нам известны осевые моменты инерции относительно этих осей 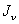 ,
, 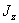 , а также центробежный момент инерции
, а также центробежный момент инерции 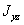 .Начертим вторую систему координатных осей
.Начертим вторую систему координатных осей 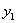 и
и 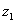 наклоненных к первым под углом
наклоненных к первым под углом 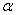 ; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей
; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей 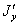 и
и 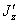 , через известные моменты инерции
, через известные моменты инерции 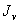 и
и 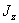 .
.
Напишем выражения для моментов инерции относительно этих осей:
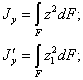 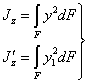 | (3) |
Из чертежа видно, что координаты площадки dF в системе повернутых осей 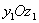 будут:
будут:
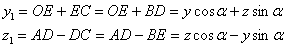
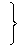
Подставляя эти значения 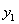 и
и 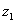 в формулы (14.9), получим:
в формулы (14.9), получим:
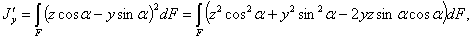
или
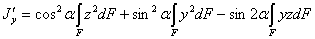 | (4) |
Аналогично:
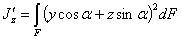
или
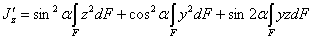 | (5) |
Первые два интеграла выражений (4) и (5) представляют собой осевые моменты инерции 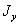 и
и 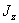 , а последний — центробежный момент инерции площади относительно этих осей
, а последний — центробежный момент инерции площади относительно этих осей 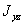 . Тогда:
. Тогда:
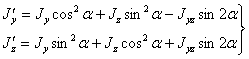 | (6) |
Для решения задач могут понадобиться формулы перехода от одних осей к другим для центробежного момента инерции. При повороте осей (Рис.2) имеем:
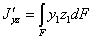
где 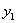 и
и 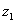 вычисляются по формулам (14.10); тогда
вычисляются по формулам (14.10); тогда
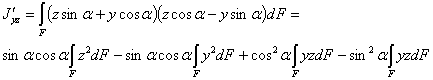
После преобразований получим:
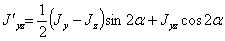 | (7) |
Таким образом, для того чтобы вычислить момент инерции относительно любой центральной оси 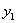 , надо знать моменты инерции
, надо знать моменты инерции 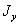 и
и 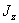 относительно системы каких-нибудь двух взаимно перпендикулярных центральных осей Оу и Oz, центробежный момент инерции
относительно системы каких-нибудь двух взаимно перпендикулярных центральных осей Оу и Oz, центробежный момент инерции 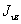 относительно тех же осей и угол наклона оси
относительно тех же осей и угол наклона оси 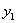 к оси у.
к оси у.
Для вычисления же величин 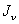 >
> 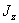 ,
, 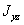 приходится так выбирать оси у и z и разбивать площадь фигуры на такие составные части, чтобы иметь возможность произвести это вычисление, пользуясь только формулами перехода от центральных осей каждой из составных частей к осям, им параллельным. Как это сделать на практике, будет показано ниже на примере. Заметим, что при этом вычислении сложные фигуры надо разбивать на такие элементарные части, для которых по возможности известны величины центральных моментов инерции относительно системы взаимно перпендикулярных осей.
приходится так выбирать оси у и z и разбивать площадь фигуры на такие составные части, чтобы иметь возможность произвести это вычисление, пользуясь только формулами перехода от центральных осей каждой из составных частей к осям, им параллельным. Как это сделать на практике, будет показано ниже на примере. Заметим, что при этом вычислении сложные фигуры надо разбивать на такие элементарные части, для которых по возможности известны величины центральных моментов инерции относительно системы взаимно перпендикулярных осей.
Заметим, что ход вывода и полученные результаты не изменились бы, если бы начало координат было взято не в центре тяжести сечения, а в любой другой точке О. Таким образом, формулы (6) и (7) являются формулами перехода от одной системы взаимно-перпендикулярных осей к другой, повернутой на некоторый угол 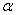 , независимо от того, центральные это оси или нет.
, независимо от того, центральные это оси или нет.
Из формул (6) можно получить еще одну зависимость между моментами инерции при повороте осей. Сложив выражения для 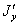 и
и 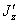 получим
получим
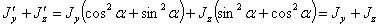
т. е. сумма моментов инерции относительно любых взаимно перпендикулярных осей у и z не меняется при их повороте. Подставляя последнее выражение вместо 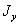 и
и 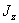 их значения, получим:
их значения, получим:
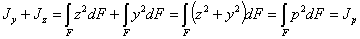
где 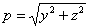 — расстояние площадок dF от точки О. Величина
— расстояние площадок dF от точки О. Величина 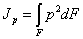 является, как уже известно, полярным моментом инерции сечения относительно точки О.
является, как уже известно, полярным моментом инерции сечения относительно точки О.
Таким образом, полярный момент инерции сечения относительно какой-либо точки равен сумме осевых моментов инерции относительно взаимно перпендикулярных осей, проходящих через эту точку. Поэтому эта сумма и остается постоянной при повороте осей. Этой зависимостью (14.16) можно пользоваться для упрощения вычисления моментов инерции. Так, для круга:
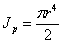
Так как по симметрии для круга 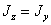 то
то
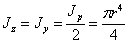
что было получено выше путем интегрирования.
Точно также для тонкостенного кольцевого сечения можно получить:
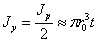
Лекция № 18. Главные оси инерции и главные моменты инерции.
Как уже известно, зная для данной фигуры центральные моменты инерции 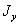 ,
, 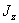 и
и 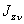 , можно вычислить момент инерции и относительно любой другой оси.
, можно вычислить момент инерции и относительно любой другой оси.
При этом можно за основную систему осей принять такую систему, при которой формулы существенно упрощаются. Именно, можно найти систему координатных осей, для которых центробежный момент инерции равен.нулю. В самом деле, моменты инерции 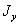 и
и 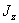 всегда положительны, как суммы положительных слагаемых, центробежный же момент
всегда положительны, как суммы положительных слагаемых, центробежный же момент
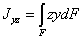
может быть и положительным и отрицательным, так как слагаемые zydF могут быть разного знака в зависимости от знаков z и у для той или иной площадки. Значит, он может быть равен нулю.
Оси, относительно которых центробежный момент инерции обращается в нуль, называются главными осями инерции. Если начало такой системы помещено в центре тяжести фигуры, то это будут главные центральные оси. Эти оси мы будем обозначать 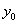 и
и 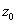 ; для них
; для них
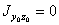
Найдем, под каким углом 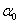 наклонены к центральным осям у и z (фиг. 198) главные оси.
наклонены к центральным осям у и z (фиг. 198) главные оси.

Рис.1. Расчетная модель для определения положения главных осей инерции.
В известном выражении для перехода от осей yz к осям 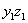 , для центробежного момента инерции дадим углу
, для центробежного момента инерции дадим углу 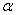 значение
значение 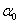 ; тогда оси
; тогда оси 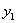 и
и 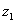 , совпадут c главными, и центробежный момент инерции будет равен нулю:
, совпадут c главными, и центробежный момент инерции будет равен нулю:
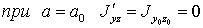
или
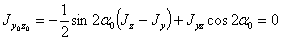
откуда:
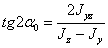 | (1) |
Этому уравнению удовлетворяют два значения 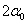 , отличающиеся на 180°, или два значения
, отличающиеся на 180°, или два значения 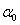 , отличающиеся на 90°. Таким образом, это уравнение дает нам положение двух осей, составляющих между собой прямой угол. Это и будут главные центральные оси
, отличающиеся на 90°. Таким образом, это уравнение дает нам положение двух осей, составляющих между собой прямой угол. Это и будут главные центральные оси 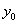 и
и 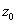 , для которых
, для которых 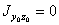 .
.
Пользуясь этой формулой, можно по известным 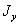 ,
, 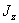 и
и 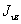 получить формулы для главных моментов инерции
получить формулы для главных моментов инерции 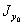 и
и 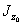 . Для этого опять воспользуемся выражениями для осевых моментов инерции общего положения. Они определяют значения
. Для этого опять воспользуемся выражениями для осевых моментов инерции общего положения. Они определяют значения 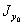 и
и 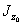 если вместо
если вместо 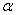 подставить
подставить 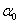
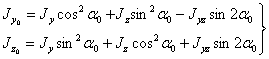 | (2) |
Полученными соотношениями можно пользоваться при решении задач. Одним из главных моментов инерции является 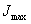 , другим
, другим 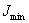 .
.
Формулы (2) можно преобразовать к виду, свободному от значения 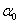 . Выражая
. Выражая 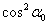 и
и 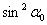 через
через 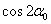 и подставляя их значения в первую формулу (2), получим, делая одновременно замену
и подставляя их значения в первую формулу (2), получим, делая одновременно замену 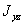 из формулы (1):
из формулы (1):
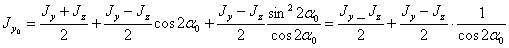
Заменяя здесь из формулы (1) дробь 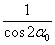 на
на
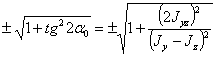
получаем
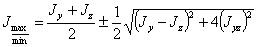 | (3) |
К этому же выражению можно прийти, делая подобное же преобразование второй формулы (3).
За основную систему центральных осей, от которых можно переходить к любой другой, можно взять не Оу и Oz, а главные оси 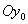 и
и 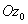 ; тогда в формулах не будет фигурировать центробежный момент инерции (
; тогда в формулах не будет фигурировать центробежный момент инерции ( 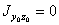 ). Обозначим угол, составленный осью
). Обозначим угол, составленный осью 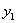 , (Рис.2) с главной осью
, (Рис.2) с главной осью 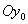 , через
, через 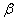 . Для вычисления
. Для вычисления 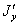 ,
, 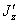 и
и 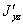 , переходя от осей
, переходя от осей 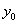 и
и 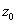 нужно в ранее найденных выражениях для
нужно в ранее найденных выражениях для 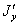 ,
, 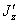 и
и 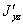 , заменить угол
, заменить угол 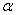 через
через 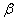 , а
, а 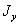 ,
, 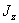 и
и 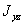 — через
— через 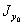 ,
, 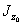 и
и 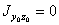 . В результате получаем:
. В результате получаем:
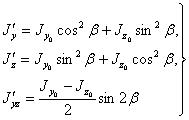
По своему виду эти формулы совершенно аналогичны формулам для нормальных 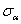 и касательных
и касательных 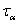 напряжений по двум взаимно-перпендикулярным площадкам в элементе, подвергающемся растяжению в двух направлениях. Укажем лишь формулу, позволяющую из двух значений угла
напряжений по двум взаимно-перпендикулярным площадкам в элементе, подвергающемся растяжению в двух направлениях. Укажем лишь формулу, позволяющую из двух значений угла 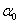 выделить то, которое соответствует отклонению первой главной оси (дающей max J) от начального положения оси у:
выделить то, которое соответствует отклонению первой главной оси (дающей max J) от начального положения оси у:
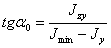
Теперь можно окончательно формулировать, что надо сделать, чтобы получить возможность простейшим образом вычислять момент инерции фигуры относительно любой оси. Необходимо через центр тяжести фигуры провести оси Оу и Oz так, чтобы, разбивая фигуру на простейшие части, мы могли легко вычислить моменты 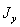 ,
, 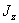 и
и 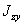 после этого следует найти по формуле (14.17) величину угла
после этого следует найти по формуле (14.17) величину угла 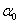 и вычислить главные центральные моменты инерции
и вычислить главные центральные моменты инерции 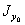 и
и 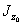 по формулам (14.18).
по формулам (14.18).

Рис.2. Расчетная модель нахождения положения главных осей.
Далее, можно найти момент инерции относительно любой центральной оси 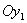 (Рис.2), наклоненной к
(Рис.2), наклоненной к 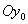 под углом
под углом 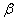 :
:
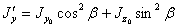
Зная же центральный момент инерции 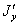 , можно сейчас же найти момент инерции относительно любой параллельной ей оси
, можно сейчас же найти момент инерции относительно любой параллельной ей оси 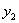 , проходящей на расстоянии
, проходящей на расстоянии 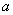 (рис.2) от центра тяжести:
(рис.2) от центра тяжести:
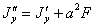
Во многих случаях удается сразу провести главные оси фигуры; если фигура имеет ось симметрии, то это и будет одна из главных осей. В самом деле, при выводе формулы 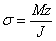 мы уже имели дело с интегралом
мы уже имели дело с интегралом 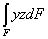 , представляющим собой центробежный момент инерции сечения относительно осей у и z; было доказано, что если ось Oz является осью симметрии, этот интеграл обращается в нуль.
, представляющим собой центробежный момент инерции сечения относительно осей у и z; было доказано, что если ось Oz является осью симметрии, этот интеграл обращается в нуль.
Стало быть, в данном случае оси Оу и Oz являются главными центральными осями инерции сечения. Таким образом, ось симметрии — всегда главная центральная ось; вторая главная центральная ось проходит через центр тяжести перпендикулярно к оси симметрии.
Пример. Найти моменты инерции прямоугольника (Рис.3) относительно осей 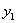 и
и 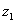 и центробежный момент его относительно тех же осей.
и центробежный момент его относительно тех же осей.
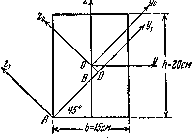
Рис.3. Пример расчета моментов инерции.
Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны:
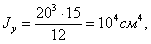
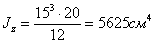
Центральные моменты относительно повернутых осей 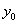 и
и 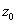 равны:
равны:
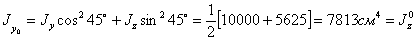
Центробежный момент инерции относительно осей 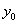 и
и 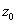 равен:
равен:
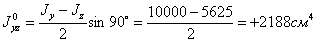
Координаты центра тяжести прямоугольника относительно осей 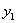 и
и 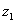 равны:
равны:
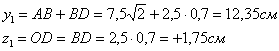
Моменты инерции относительно осей 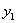 и
и 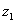 равны:
равны:
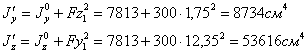
Центробежный момент инерции равен: