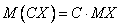Неоднородная система линейных уравнений
может быть несовместной
Неоднородная система линейных уравнений 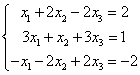
имеет частное решениех(0, 1, 0), имеет частное решениех(-1.2, 2.6, 1), совместна
Несмещенная оценка для дисперсии вычисляется по эмпирической дисперсии S2по формуле:A) 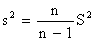 ,B)
,B) 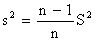 ,C)
,C) 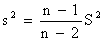 ,D)
,D) 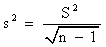
A
Нормированным вектором называется вектор
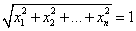 , длина которого равна 1, модуль которого равен 1
, длина которого равна 1, модуль которого равен 1
Однородная система линейных уравнений
всегда совместна, имеет хотя бы тривиальное решение 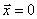
Окружность можно рассматривать как частный случай эллипса с ______ полуосями
равными
Определители матриц и равны
5и 4
Определители матриц и равны
det A=3, det B=-7
Ордината трехмерного вектора 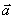 (1,3,2) равна______
(1,3,2) равна______
Параметр случайной величины 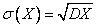 называется среднеквадратическим ___________
называется среднеквадратическим ___________
отклонением
Представление вектора 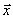 в виде линейной комбинации линейно-независимых векторов
в виде линейной комбинации линейно-независимых векторов 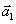 ,
, 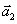 ,.,
,., 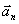
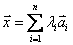 ,
, 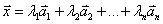 , называется разложением вектора
, называется разложением вектора 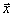 по базису
по базису 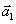 ,
, 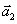 ,…
,… 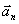
Преобразование матрицы системы линейных уравнений в ступенчатую называется ________ ходом метода Гаусса
прямым
При проведении расчетов для двух выборок получили два коэффициента корреляции. Ошибки допущено не было. Значения r1и r2составили
-0,54; 0,76
Проведено 10 измерений и по ним вычислена эмпирическая дисперсия S2=4,5. Несмещенная оценка для генеральной дисперсии равна
Прямоугольную систему координат предложил известный французский математик __________
Декарт
Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице: Эмпирическое среднее времени, затрачиваемого на обработку одной детали, эмпирическая дисперсия и среднеквадратическое отклонение составляют соответственно
7,4; 4,24; 2,06
Распределение дискретной случайной величины такое, что 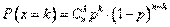 называется ____________
называется ____________
биномиальным
Распределение дискретной случайной величины такое, что 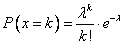 называется _____________
называется _____________
пуассоновским
Распределение случайной величины такое, что 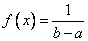 для
для 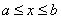 и
и 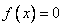 для
для 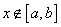 называется ___________
называется ___________
равномерным
Распределение случайной величины такое, что 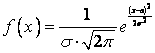 для
для 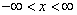
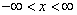 называется ___________
называется ___________
нормальным
Решение, состоящее из суммы общего решения однородной системы и любого частного решения неоднородной системы, представляет собой общее решение ____________ системы линейных уравнений
неоднородной
Свойства дисперсии:
дисперсия постоянной величины равна нулю == 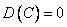 , дисперсия произведения случайной величины на постоянную есть ==
, дисперсия произведения случайной величины на постоянную есть == 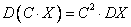 , дисперсия случайной величины всегда положительна ==
, дисперсия случайной величины всегда положительна == 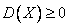 , при суммировании случайной величины с постоянной дисперсия суммы не изменяется ==
, при суммировании случайной величины с постоянной дисперсия суммы не изменяется == 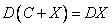
Свойства математического ожидания:
для независимых случайных величин 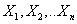 ==
== 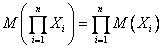 , для постоянной величины ==
, для постоянной величины == 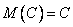 , мат. ожидание произведения случайной величины на постоянную есть ==
, мат. ожидание произведения случайной величины на постоянную есть ==