Мгновенный центр ускорений
В каждый момент движения плоской фигуры в своей плоскости, если 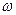 и
и 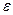 не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. Обозначим ее через
не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений. Обозначим ее через 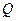 . Пусть
. Пусть 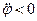 (рис. 39). Мгновенный центр ускорений лежит на линии, проведенной под углом
(рис. 39). Мгновенный центр ускорений лежит на линии, проведенной под углом 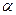 к ускорению точки, тангенс которого вычисляем по формуле:
к ускорению точки, тангенс которого вычисляем по формуле:
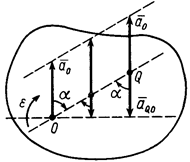
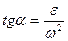 .
.
 При этом угол
При этом угол 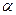 надо отложить от ускорения
надо отложить от ускорения 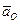 в направлении дуговой стрелки углового ускорения
в направлении дуговой стрелки углового ускорения 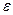 , т.е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение
, т.е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение 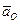 и ускорение от вращения
и ускорение от вращения 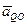 могут иметь противоположные направления и одинаковые значения, т.е.:
могут иметь противоположные направления и одинаковые значения, т.е.:
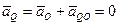 , и тогда
, и тогда
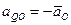 .
.
Но 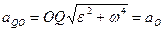 , следовательно,
, следовательно,
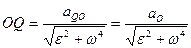 .
.
Мгновенный центр ускорений является единственной точкой плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если мгновенный центр ускорений известен, то, выбрав его за полюс, для ускорения точки 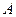 плоской фигуры по формуле (93) получаем
плоской фигуры по формуле (93) получаем
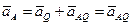 , т.к.
, т.к. 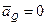 .
.
Следовательно:
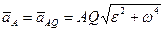 . (99)
. (99)
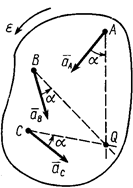 Ускорение
Ускорение 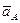 направлено под углом
направлено под углом 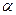 к отрезку
к отрезку 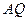 , соединяющему точку
, соединяющему точку 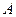 с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения
с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения 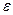 (рис. 40).
(рис. 40).
Для точки 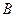 аналогично
аналогично
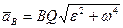 (100)
(100)
и ускорение 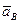 также направлено под углом
также направлено под углом 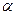 к отрезку
к отрезку 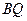
 Из формул (99) и (100) имеем
Из формул (99) и (100) имеем
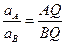 , (101)
, (101)
т.е. ускорения точек плоской фигуры при плоском движении пропорциональны расстояниям от этих точек до мгновенного центра ускорений.
Итак, суммируя результаты, получаем, что ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью 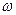 и угловым ускорением
и угловым ускорением 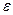 .
.
Для вычисления скоростей точек плоской фигуры при плоском движении принимают, что плоская фигура вращается вокруг мгновенного центра скоростей, а для вычисления ускорения следует считать, что она вращается вокруг мгновенного центра ускорений.
Решение задач кинематики
Пример 3.
Даны уравнения движения точки в плоскости 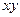 :
:
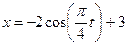 ,
, 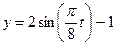
( 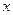 ,
, 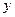 – в сантиметрах,
– в сантиметрах, 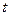 – в секундах).
– в секундах).
Определить: уравнение траектории точки; для момента времени 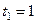 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение:
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время 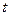 . Поскольку
. Поскольку 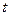 входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
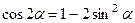 :
:
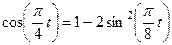 . (102)
. (102)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (102). Получим
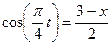 ,
,
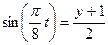 ,
,
следовательно,
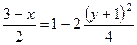 .
.
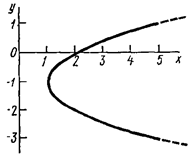
 Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):
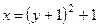 . (103)
. (103)
2. Скорость точки найдем по ее проекциям на координатные оси:
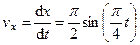 ,
, 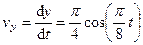 ,
,
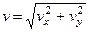 .
.
Для момента времени 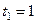 с:
с: 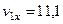
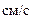 ,
, 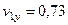
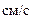 ,
, 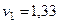
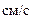 . (104)
. (104)
3. Аналогично найдем ускорение точки:
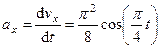 ,
, 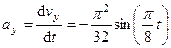 ,
,
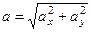 .
.
Для момента времени 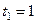 с:
с: 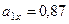
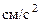 ,
, 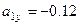
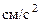 ,
, 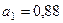
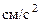 . (105)
. (105)
4. Касательное ускорение найдем, дифференцируя по времени равенство:
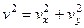
Получим
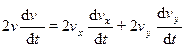 ,
,
откуда
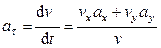 . (106)
. (106)
Числовые значения всех величин, входящих в правую часть (106), определены и даются в (104) и (105). Подставив в (106) эти числа, найдем сразу, что при 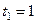 с:
с: 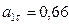
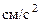 .
.
5. Нормальное ускорение точки 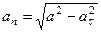 . Подставляя сюда найденные при
. Подставляя сюда найденные при 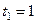 с числовые значения
с числовые значения 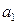 и
и 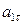 , получим, что
, получим, что 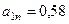
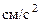 .
.
6. Радиус кривизны траектории 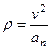 .
.
Подставляя сюда числовые значения 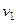 и
и 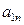 при
при 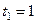 с, найдем, что
с, найдем, что 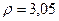 см.
см.
Ответ: 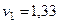
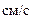 ,
, 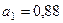
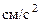 ,
, 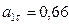
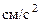 ,
, 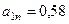
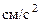 ,
, 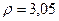 см.
см.
 Пример 4.
Пример 4. 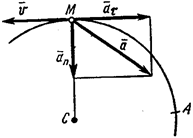 Точка движется по дуге окружности радиуса
Точка движется по дуге окружности радиуса 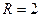 м по закону
м по закону 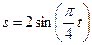 , (
, ( 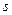 – в метрах,
– в метрах, 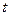 – в секундах), где
– в секундах), где 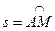 (рис. 42).
(рис. 42).
Определить: скорость и ускорение точки в момент времени 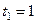 с.
с.
Решение:
Определяем скорость точки:
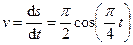 .
.
При 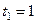 с получим
с получим 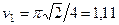
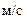 .
.
Ускорение находим по его касательной и нормальной составляющим:
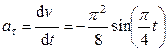 ,
, 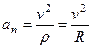 ,
, 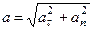 .
.
При 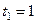 с получим
с получим 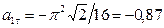
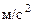 ,
, 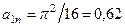
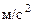 ,
, 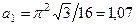
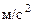 .
.
Изобразим на рис. 42 векторы 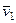 и
и 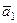 , учитывая знаки и считая положительным направление от
, учитывая знаки и считая положительным направление от 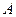 к
к  .
.
Ответ: 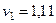
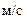 ,
, 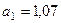
 .
.
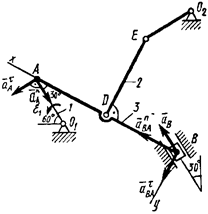
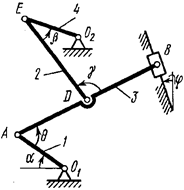 Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна
Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами.
шарнирами.

 Дано:
Дано: 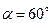 ,
, 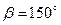 ,
, 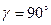 ,
, 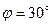 ,
, 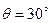 ,
, 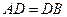 ,
, 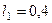 м,
м,  м,
м, 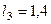 м,
м, 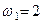 с-1,
с-1, 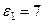 с-2 (направления
с-2 (направления 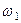 и
и 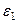 – против хода часовой стрелки).
– против хода часовой стрелки).
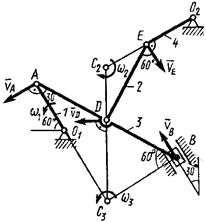 Определить:
Определить: 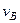 ,
, 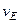 ,
, 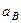 ,
, 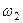 ,
, 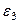 .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. 44; на этом рисунке изображаем все векторы скоростей).
 2. Определяем
2. Определяем 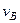 . Точка
. Точка 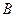 принадлежит стержню
принадлежит стержню 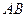 . Чтобы найти
. Чтобы найти 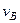 , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление 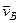 . По данным задачи, учитывая направление
. По данным задачи, учитывая направление 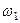 , можем определить
, можем определить 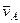 . Численно:
. Численно:
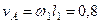 м/с,
м/с,
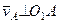 . (107)
. (107)
Направление 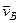 найдем, учтя, что точка
найдем, учтя, что точка 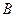 принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 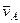 и направление
и направление 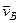 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 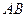 ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая 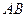 ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 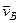 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
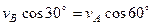 ,
, 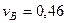 м/с. (108)
м/с. (108)
3. Определяем 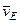 . Точка
. Точка 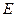 принадлежит стержню
принадлежит стержню 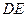 . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить 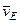 , надо сначала найти скорость точки
, надо сначала найти скорость точки 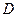 , принадлежащей одновременно стержню
, принадлежащей одновременно стержню 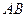 . Для этого, зная
. Для этого, зная 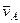 и
и 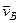 , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня 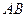 . Это точка
. Это точка 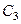 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к 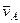 и
и 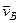 , восставленных из точек
, восставленных из точек 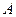 и
и 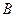 (к
(к 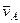 перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора 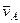 определяем направление поворота стержня
определяем направление поворота стержня 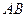 вокруг МЦС
вокруг МЦС 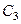 . Вектор
. Вектор 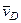 перпендикулярен отрезку
перпендикулярен отрезку 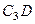 , соединяющему точки
, соединяющему точки 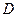 и
и 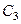 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину 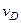 найдем из пропорции:
найдем из пропорции:
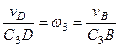 . (109)
. (109)
Чтобы вычислить 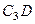 и
и 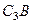 , заметим, что
, заметим, что 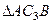 – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что 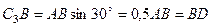 . Тогда
. Тогда 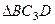 является равносторонним и
является равносторонним и 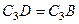 . В результате равенство (3) дает
. В результате равенство (3) дает
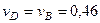 м/с,
м/с, 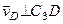 . (110)
. (110)
Так как точка 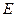 принадлежит одновременно стержню
принадлежит одновременно стержню 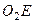 , вращающемуся вокруг
, вращающемуся вокруг 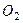 , то
, то 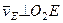 . Тогда, восставляя из точек
. Тогда, восставляя из точек 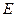 и
и 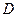 перпендикуляры к скоростям
перпендикуляры к скоростям 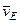 и
и 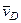 , построим МЦС
, построим МЦС 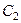 стержня
стержня 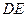 . По направлению вектора
. По направлению вектора 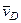 определяем направление поворота стержня
определяем направление поворота стержня 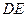 вокруг центра
вокруг центра 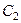 . Вектор
. Вектор 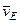 направлен в сторону поворота этого стержня. Из рис. 44 видно, что
направлен в сторону поворота этого стержня. Из рис. 44 видно, что 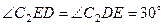 , откуда
, откуда 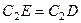 . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
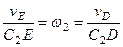 ,
, 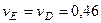 м/с. (110)
м/с. (110)
4. Определяем 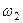 . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка 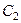 ) и
) и 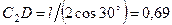 м, то
м, то
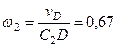 с–1. (111)
с–1. (111)

 5. Определяем
5. Определяем 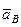 (рис. 45, на котором изображаем все векторы ускорений). Точка
(рис. 45, на котором изображаем все векторы ускорений). Точка 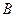 принадлежит стержню
принадлежит стержню 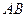 . Чтобы найти
. Чтобы найти 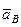 , надо знать ускорение какой-нибудь другой точки стержня
, надо знать ускорение какой-нибудь другой точки стержня 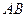 и траекторию точки
и траекторию точки 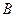 . По данным задачи можем определить
. По данным задачи можем определить 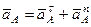 , где численно
, где численно
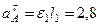 м/с2,
м/с2,
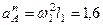 м/с2. (112)
м/с2. (112)
Вектор 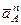 направлен вдоль
направлен вдоль 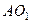 , а
, а 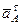 – перпендикулярно
– перпендикулярно 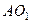 . Изображаем эти векторы на чертеже (см. рис. 45). Так как точка
. Изображаем эти векторы на чертеже (см. рис. 45). Так как точка 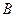 одновременно принадлежит ползуну, то вектор
одновременно принадлежит ползуну, то вектор 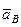 параллелен направляющим ползуна. Изображаем вектор
параллелен направляющим ползуна. Изображаем вектор 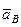 на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 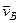 .
.
Для определения 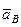 воспользуемся равенством
воспользуемся равенством
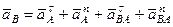 . (113)
. (113)
Изображаем на чертеже векторы 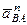 (вдоль
(вдоль 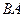 от
от 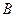 к
к 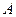 ) и
) и 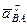 (в любую сторону перпендикулярно
(в любую сторону перпендикулярно 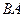 ). Численно
). Численно 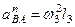 Найдя
Найдя 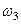 с помощью построенного МЦС
с помощью построенного МЦС 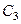 стержня 3, получим
стержня 3, получим
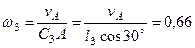 с–1,
с–1, 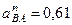 м/с2. (114)
м/с2. (114)
Таким образом, у величин, входящих в равенство (113), неизвестны только числовые значения 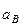 и
и 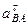 . Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.
. Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.
Чтобы определить 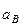 , спроектируем обе части равенства (113) на направление
, спроектируем обе части равенства (113) на направление 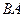 (ось
(ось 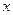 ). Тогда получим
). Тогда получим
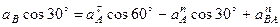 . (115)
. (115)
Подставив в равенство (10) числовые значения всех величин из (112) и (114), найдем, что
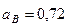 м/с2. (116)
м/с2. (116)
Так как получилось 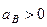 , то, следовательно, вектор
, то, следовательно, вектор 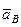 направлен как показано на рис. 45.
направлен как показано на рис. 45.
6. Определяем 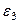 . Чтобы найти
. Чтобы найти 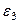 , сначала определим
, сначала определим 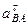 . Для этого обе части равенства (113) спроектируем на направление, перпендикулярное
. Для этого обе части равенства (113) спроектируем на направление, перпендикулярное 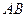 (ось
(ось 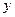 ). Тогда получим:
). Тогда получим:
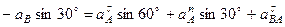 . (117)
. (117)
Подставив в равенство (12) числовые значения всех величин из (116) и (112), найдем, что 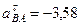 м/с2. Знак минус указывает, что направление
м/с2. Знак минус указывает, что направление 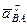 противоположно показанному на рис. 45.
противоположно показанному на рис. 45.
Теперь из равенства 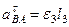 получим:
получим:
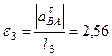 с–2.
с–2.
Ответ: 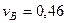 м/с,
м/с, 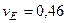 м/с,
м/с, 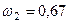 с–1,
с–1, 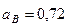 м/с2,
м/с2, 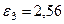 с–2.
с–2.

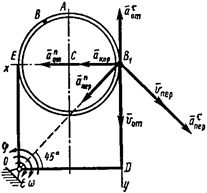 Пример 6. Пластина
Пример 6. Пластина 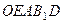 (
( 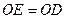 , рис. 46) вращается вокруг оси, проходящей через точку
, рис. 46) вращается вокруг оси, проходящей через точку 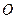 перпендикулярно плоскости пластины, по закону
перпендикулярно плоскости пластины, по закону 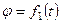 (положительное направление отсчета угла
(положительное направление отсчета угла 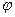 показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса
показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса 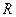 движется точка
движется точка 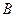 по закону
по закону 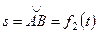 (положительное направление отсчета
(положительное направление отсчета 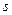 – от
– от 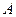 к
к 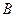 ).
).
Дано: 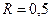 м,
м, 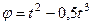 ,
, 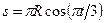 (
( 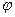 – в радианах,
– в радианах, 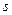 – в метрах,
– в метрах, 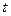 – в секундах).
– в секундах).
Определить: 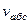 и
и 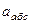 в момент времени
в момент времени 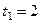 с.
с.
Решение:
Рассмотрим движение точки 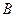 как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость
как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость 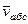 и абсолютное ускорение
и абсолютное ускорение 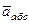 точки найдутся по формулам:
точки найдутся по формулам:
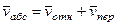 ,
, 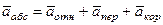 , (118)
, (118)
где, в свою очередь,
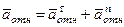 ,
, 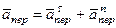 .
.
Определим все, входящие в равенства (118) величины.
1. Относительное движение. Это движение происходит по закону
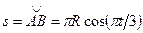 . (119)
. (119)
Сначала установим, где будет находиться точка 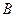 на дуге окружности в момент времени
на дуге окружности в момент времени 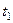 . Полагая в уравнении (119)
. Полагая в уравнении (119) 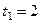 с, получим
с, получим
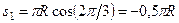 .
.
Тогда
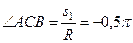 .
.
Знак минус свидетельствует о том, что точка 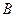 в момент
в момент 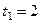 с находится справа от точки
с находится справа от точки 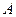 . Изображаем ее на рис. 46 в этом положении (точка
. Изображаем ее на рис. 46 в этом положении (точка 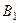 )).
)).
Теперь находим числовые значения 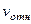 ,
, 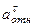 и
и 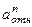 :
:
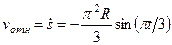 ,
,
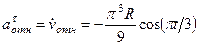 ,
, 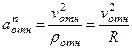 ,
,
где 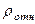 – радиус кривизны относительной траектории, равный радиусу окружности
– радиус кривизны относительной траектории, равный радиусу окружности 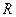 . Для момента
. Для момента 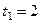 с, учитывая, что
с, учитывая, что 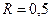 м, получим
м, получим
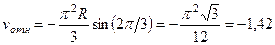 м/с,
м/с,
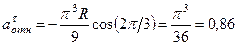 м/с2,
м/с2,
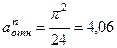 м/с2.
м/с2.
Знаки показывают, что вектор 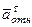 направлен в сторону положительного отсчета расстояния
направлен в сторону положительного отсчета расстояния 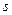 , а вектор
, а вектор 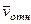 — в противоположную сторону; вектор
— в противоположную сторону; вектор 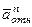 , направлен к центру
, направлен к центру 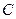 окружности. Изображаем все эти векторы на рис. 46.
окружности. Изображаем все эти векторы на рис. 46.
2. Переносное движение. Это движение (вращение) происходит по закону 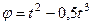 . Найдем сначала угловую скорость
. Найдем сначала угловую скорость 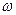 и угловое ускорение
и угловое ускорение 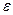 переносного вращения:
переносного вращения:
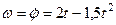 ,
, 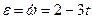
и при 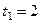 с
с
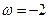 с–1 ,
с–1 , 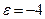 с–2. (120)
с–2. (120)
Знаки указывают, что в момент 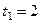 с направления
с направления 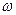 и
и 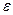 противоположны направлению положительного отсчета угла
противоположны направлению положительного отсчета угла 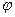 ; отметим это на рис. 46.
; отметим это на рис. 46.
Для определения 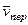 и
и 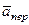 находим сначала расстояние
находим сначала расстояние 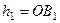 точки
точки 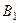 от оси вращения
от оси вращения 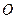 . Из рисунка видно, что
. Из рисунка видно, что 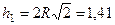 м. Тогда в момент времени
м. Тогда в момент времени 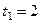 с, учитывая равенства (4), получим
с, учитывая равенства (4), получим
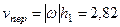 м/с,
м/с,
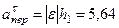 м/с2,
м/с2,
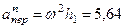 м/с2. (121)
м/с2. (121)
Изображаем на рис. 46 векторы 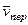 и
и 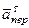 с учетом направлений
с учетом направлений 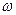 и
и 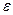 и вектор
и вектор 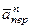 (направлен к оси вращения).
(направлен к оси вращения).
3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле
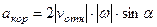 ,
,
где 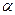 – угол между вектором
– угол между вектором 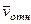 и осью вращения (вектором
и осью вращения (вектором 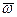 ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор
). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор 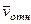 . Численно в момент времени
. Численно в момент времени 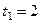 с, так как в этот момент
с, так как в этот момент 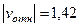 м/с,
м/с, 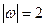 с–1, получим
с–1, получим
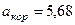 м/с2. (122)
м/с2. (122)
Направление 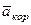 найдем по правилу Н.Е. Жуковского: так как вектор
найдем по правилу Н.Е. Жуковского: так как вектор 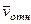 лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении
лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении 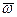 , т.е. по ходу часовой стрелки. Изображаем
, т.е. по ходу часовой стрелки. Изображаем 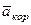 на рис. 46. (Иначе направление
на рис. 46. (Иначе направление 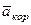 можно найти, учтя, что
можно найти, учтя, что 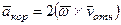 .)
.)
Таким образом, значения всех входящих в правые части равенств (118) векторов найдены и для определения 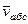 и
и 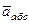 остается только сложить эти векторы. Произведем это сложение аналитически.
остается только сложить эти векторы. Произведем это сложение аналитически.
4. Абсолютная скорость. Проведем координатные оси 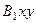 (см. рис. 46) и спроектируем почленно обе части равенства
(см. рис. 46) и спроектируем почленно обе части равенства 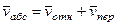 на эти оси. Получим для момента времени
на эти оси. Получим для момента времени 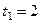 с:
с:
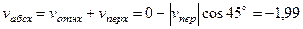 м/с,
м/с,
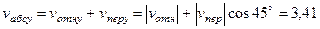 м/с.
м/с.
После этого находим
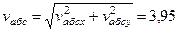 м/с.
м/с.
Учитывая, что в данном случае угол между 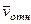 и
и 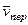 равен 45°, значение
равен 45°, значение 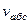 можно еще определить по формуле
можно еще определить по формуле
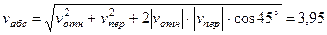 м/с.
м/с.
5. Абсолютное ускорение. По теореме о сложении ускорений
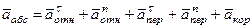 . (123)
. (123)
Для определения 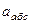 спроектируем обе части равенства (7) на проведенные оси
спроектируем обе части равенства (7) на проведенные оси 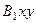 . Получим для момента времени
. Получим для момента времени 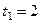 с:
с:
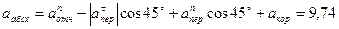 м/с2,
м/с2,
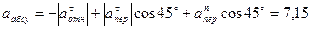 м/с2,
м/с2,
После этого находим
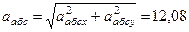 м/с2.
м/с2.
Ответ: 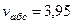 м/с,
м/с, 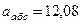 м/с2.
м/с2.
Динамика
Аксиомы динамики
I. Первая аксиома (законом классической механики, закон инерции): материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного и прямолинейного движения относительно инерциальной системы отсчета. Материальная точка, на которую не действуют силы или действует равновесная система сил, называется изолированной материальной точкой.
Равномерное и прямолинейное движение точки называют движением по инерции. Частным случаем движения по инерции является покой точки, при котором скорость ее равна нулю.
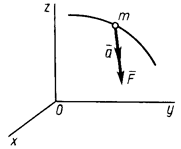 II. Вторая аксиома (основной закон динамики): ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе (рис. 47). Если
II. Вторая аксиома (основной закон динамики): ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе (рис. 47). Если 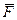 есть приложенная к точке сила и
есть приложенная к точке сила и 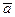 – ее ускорение относительно инерциальной системы отсчета
– ее ускорение относительно инерциальной системы отсчета 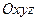 , то основной закон можно выразить в форме
, то основной закон можно выразить в форме
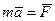 . (124)
. (124)
Положительный коэффициент пропорциональности 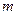 , характеризующий инертные свойства материальной точки, называется инертной массой точки. Инертная масса в классической механике считается величиной постоянной, зависящей только от самой материальной точки и не зависящей от характеристик ее движения, т.е. скорости и ускорения. Масса также не зависит от природы силы, приложенной к точке. Она одна и та же для сил тяготения, сил упругости, электромагнитных сил, сил трения и других сил.
, характеризующий инертные свойства материальной точки, называется инертной массой точки. Инертная масса в классической механике считается величиной постоянной, зависящей только от самой материальной точки и не зависящей от характеристик ее движения, т.е. скорости и ускорения. Масса также не зависит от природы силы, приложенной к точке. Она одна и та же для сил тяготения, сил упругости, электромагнитных сил, сил трения и других сил.
III. Третья аксиома (закон о равенстве сил действия и противодействия), сформулирована в статике.
IV. Четвертая аксиома (закон независимого действия сил, закон суперпозиции сил): при одновременном действии на материальную точку нескольких сил ускорение точки относительно инерциальной системы отсчета от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил. Между силами нет взаимного влияния друг на друга в создании ускорения точки. Если к материальной точке приложена система сил 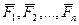 то, согласно этой аксиоме, ускорение от действия каждой из этих сил определяется по (1):
то, согласно этой аксиоме, ускорение от действия каждой из этих сил определяется по (1):
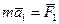 ,
, 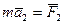 , ,
, , 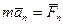 . (125)
. (125)
Ускорение при одновременном действии всех сил является векторной суммой ускорений, созданных отдельными силами, т. е
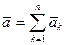 . (126)
. (126)
Суммируя (125) и используя (126), получаем основное уравнение динамики точки:
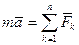 . (127)
. (127)
