Решение системы методом Жордана-Гаусса.
Семестровая работа по дисциплине
«Математика»
Тема: Линейная алгебра.
Задача 1. Решить систему линейных уравнений методом Крамера, с помощью обратной матрицы и методом Жордана-Гаусса.
1. 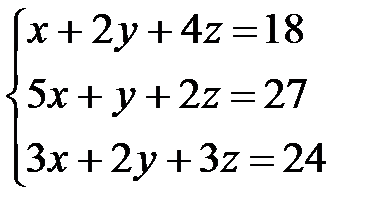 | 2. 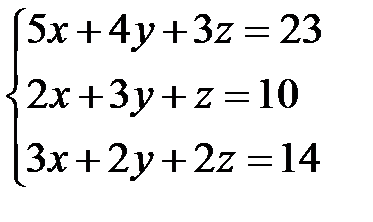 | 3.  |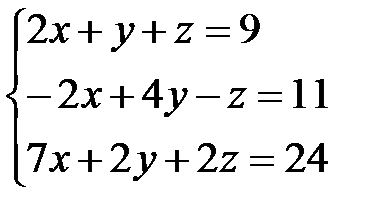
4. 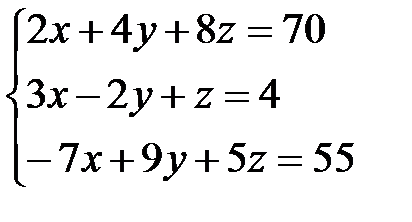 | 5. 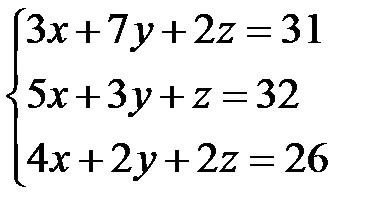 | 6.  |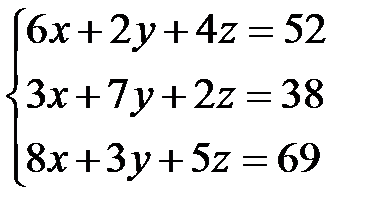
7. 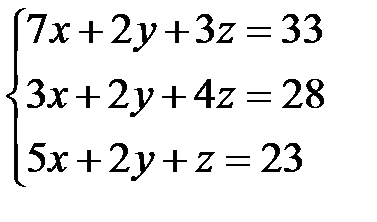 | 8. 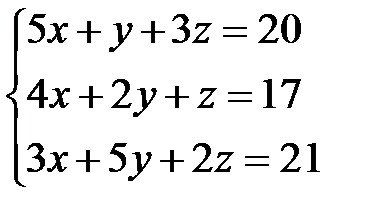 | 9.  |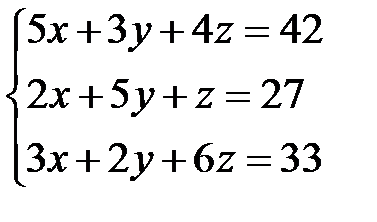
10. 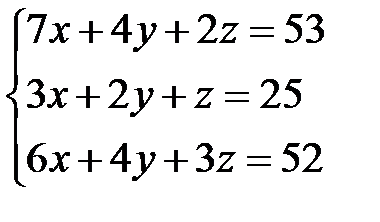 | 11. 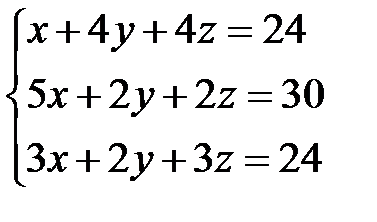 | 12.  |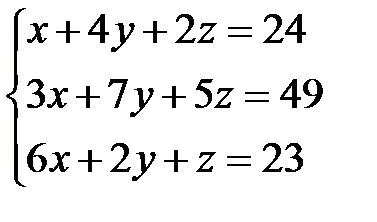
13. 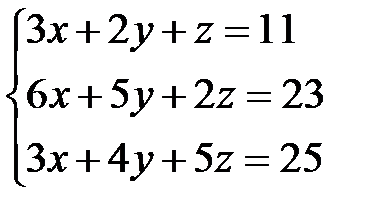 | 14. 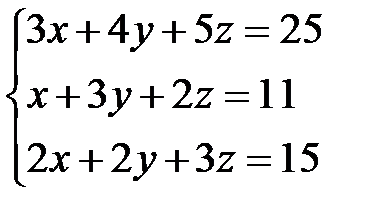 | 15.  |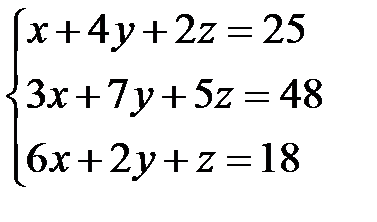
16. 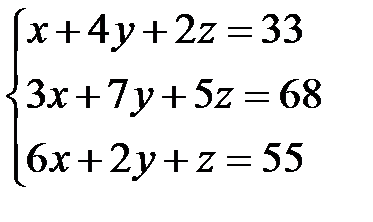 | 17. 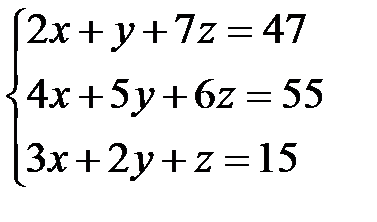 | 18.  |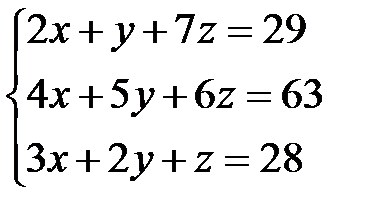
19. 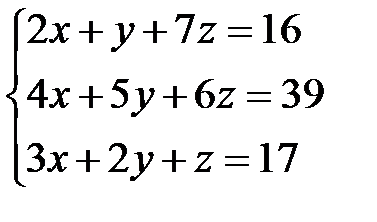 | 20. 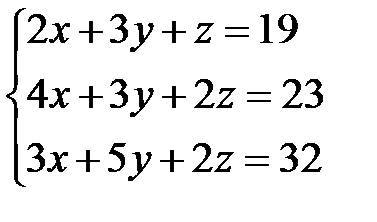 | 21.  |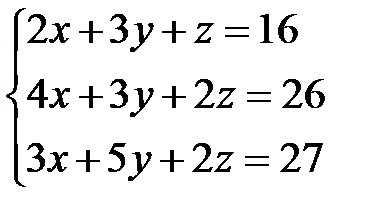
22. 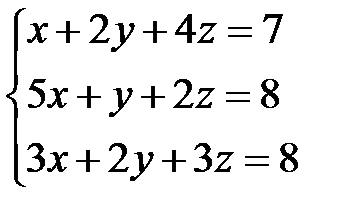 | 23. 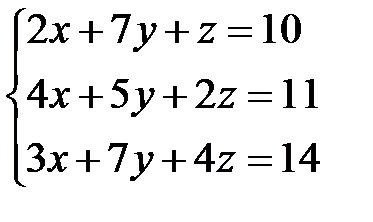 | 24.  |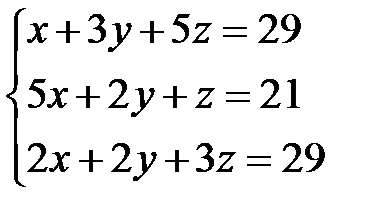
25.  |
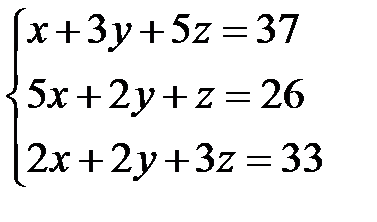Тема: Комплексные числа.
Задача 2.Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах записи комплексного числа; 2) найти все корни уравнения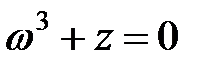 
.
1. 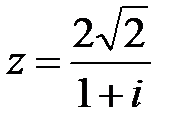 | 2. 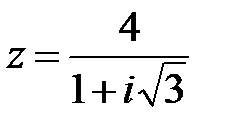 | 3.  |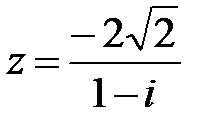
4. 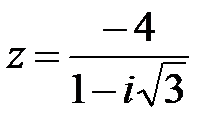 | 5. 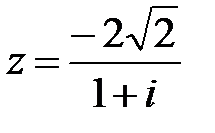 | 6.  |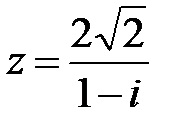
7. 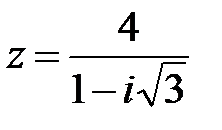 | 8. 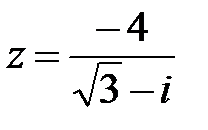 | 9.  |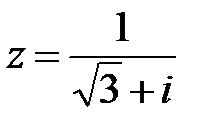
10. 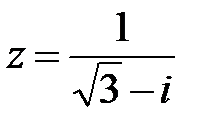 | 11. 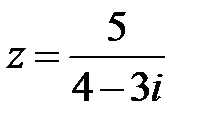 | 12.  |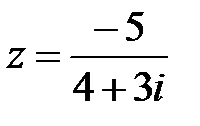
13. 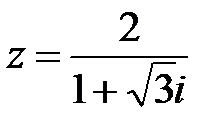 | 14. 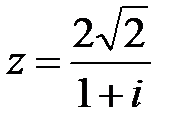| 15. |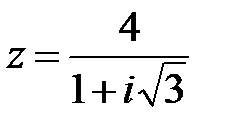
| 16. 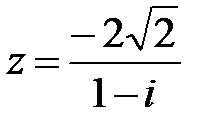| 17. 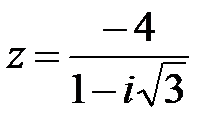| 18. |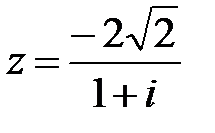
| 19. 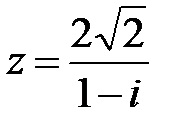| 20. 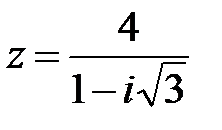| 21. |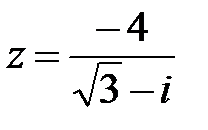
| 22. 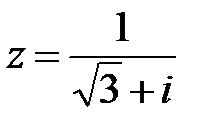| 23. 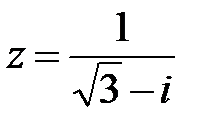| 24. |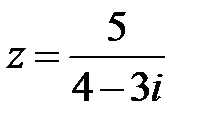
| 25. |
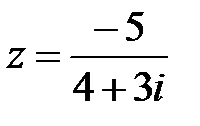Тема: Векторная алгебра.
Задача 3.Коллинеарны ли векторы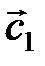 
и 
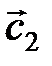, построенные по векторам 
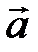и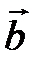 
?
1. 
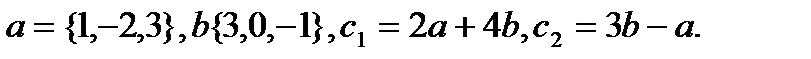
2. 
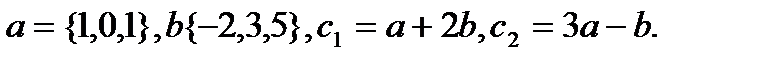
3. 
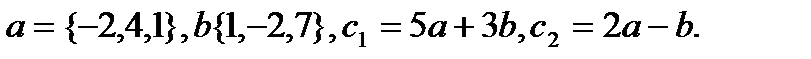
4. 
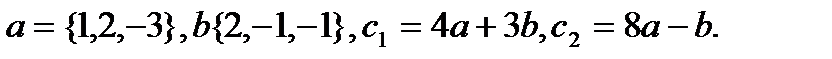
5. 
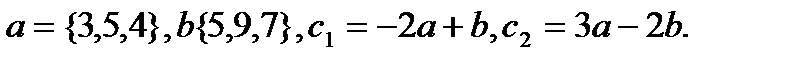
6. 
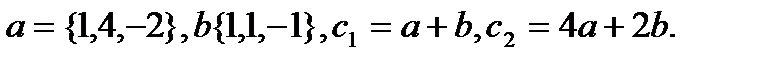
7. 
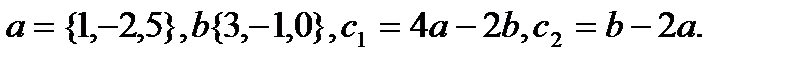
8. 
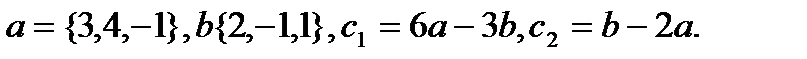
9. 
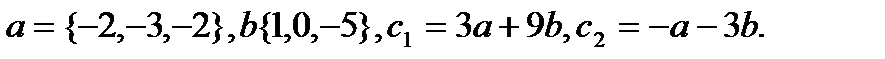
10. 
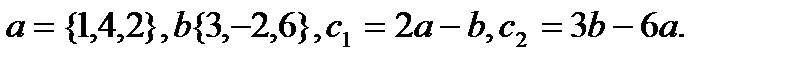
11. 
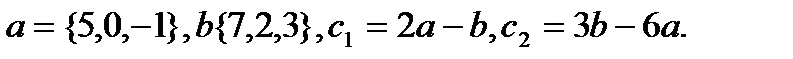
12. 
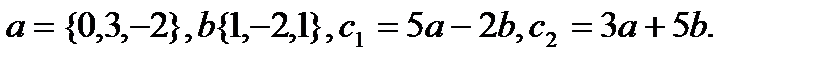
13. 
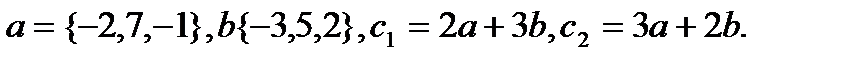
14. 
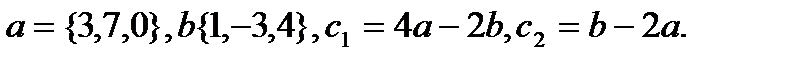
15. 
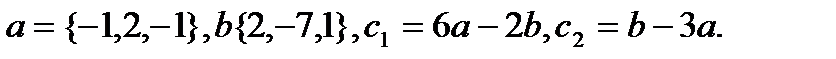
16. 
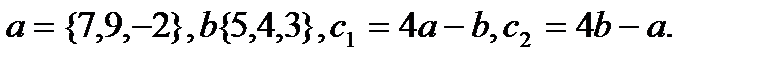
17. 
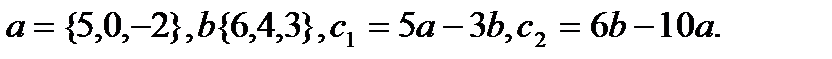
18. 
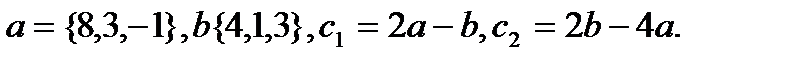
19. 
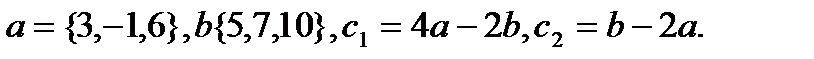
20. 
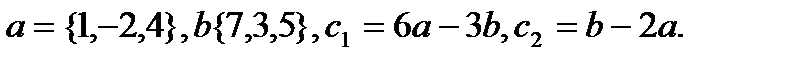
21. 
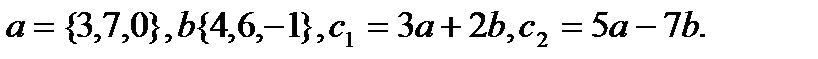
22. 
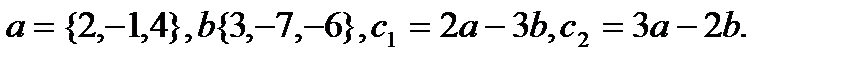
23. 
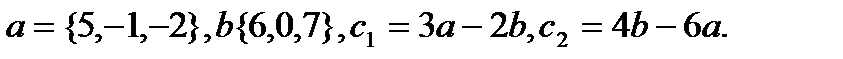
24. 
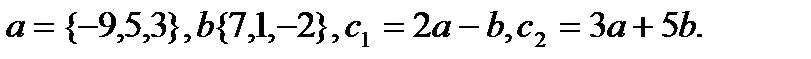
25. 
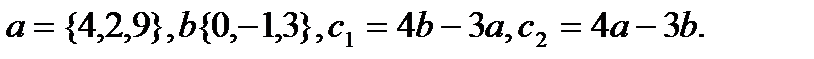
26. 
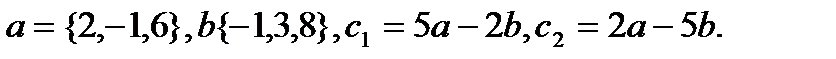
27. 
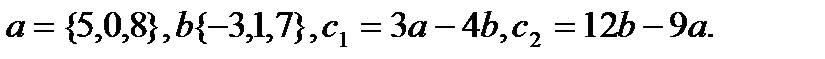
28. 
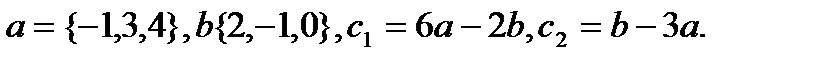
29. 
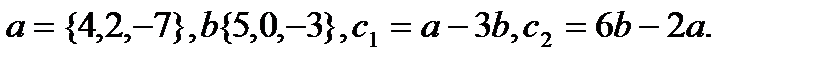
30. 
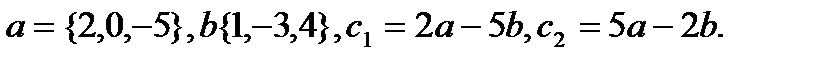
31. 
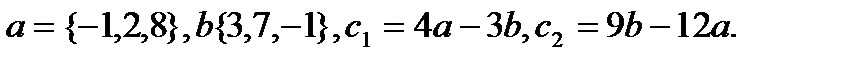
32.
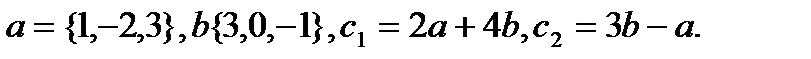
Задача 4. Найти косинус угла между векторам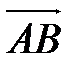и 
и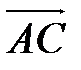 
.
1. 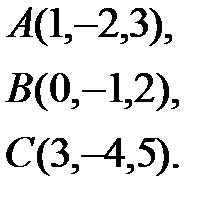 | 9. 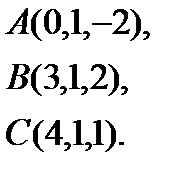 | 17. 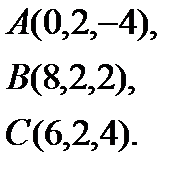 | 25.  |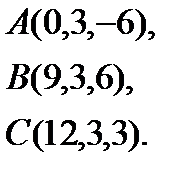
2. 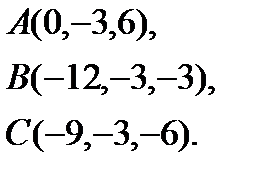 | 10. 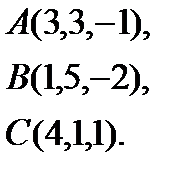 | 18. 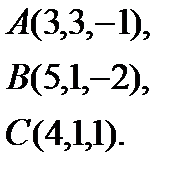 | 26.  |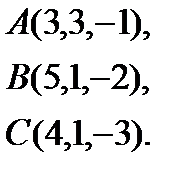
3. 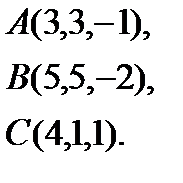 | 11. 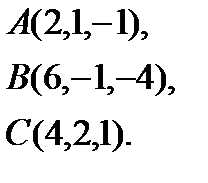 | 19. 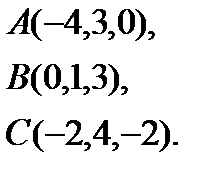 | 27.  |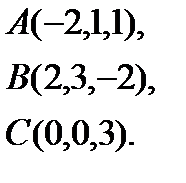
4. 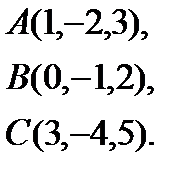 | 12. 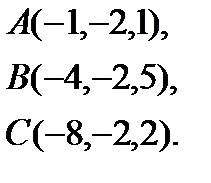 | 20. 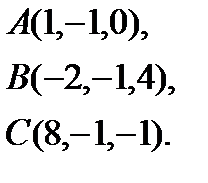 | 28.  |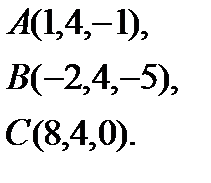
5. 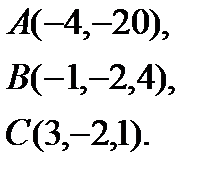 | 13. 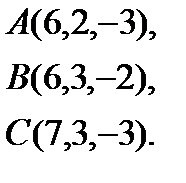 | 21. 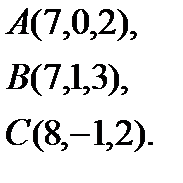 | 29.  |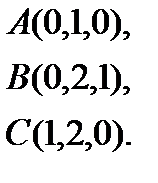
6. 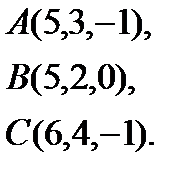 | 14. 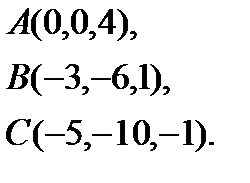 | 22. 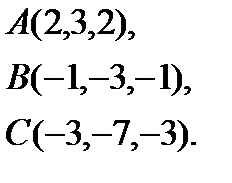 | 30.  |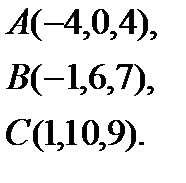
7. 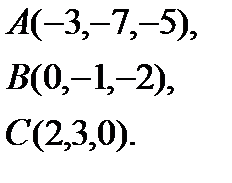 | 15. 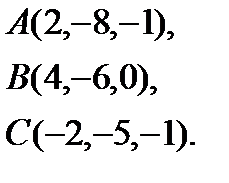 | 23. 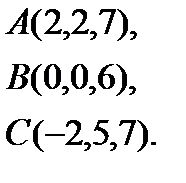 | 31.  |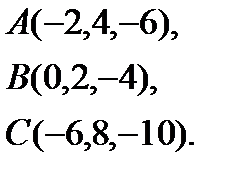
8. 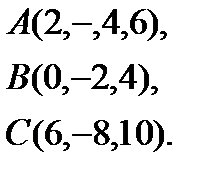 | 16. 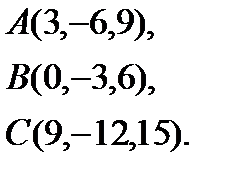 | 24. 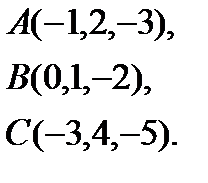 | 32. |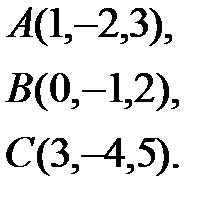
Задача 5.Вычислить площадь параллелограмма, построенного на векторах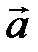 
и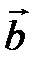 
.
1. 
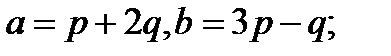
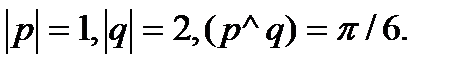
2. 
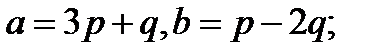
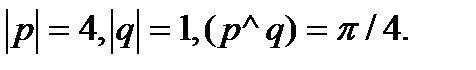
3. 
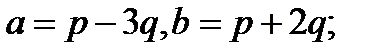
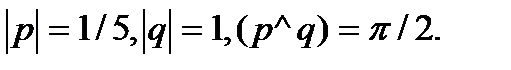
4. 
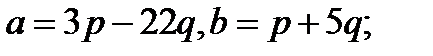
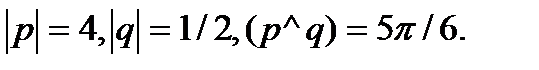
5. 
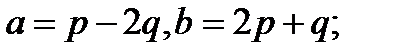
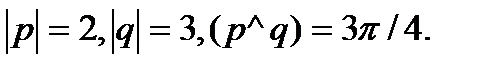
6. 
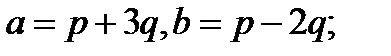
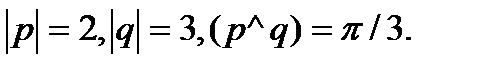
7. 
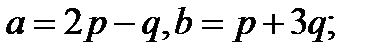
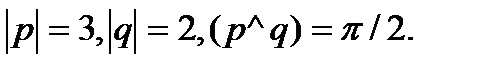
8. 
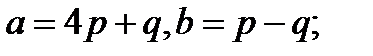
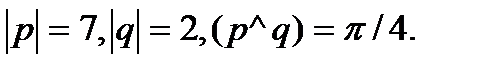
9. 
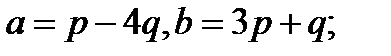
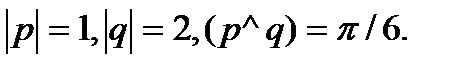
10. 
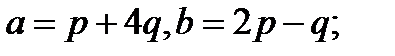
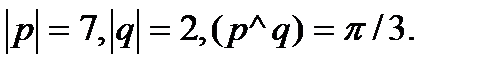
11. 
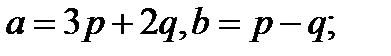
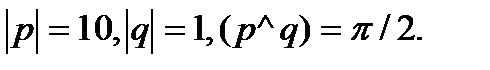
12. 
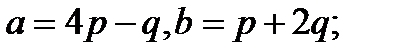
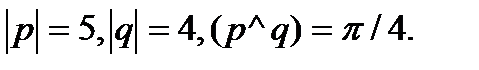
13. 
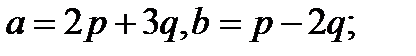
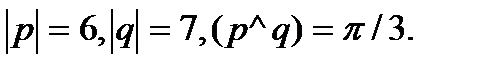
14. 
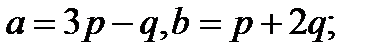
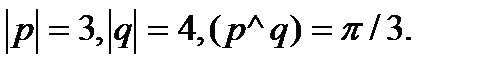
15. 
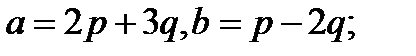
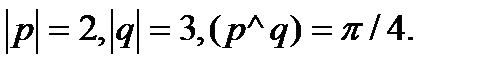
16. 
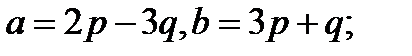
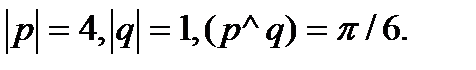
17. 
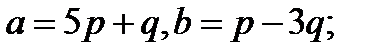
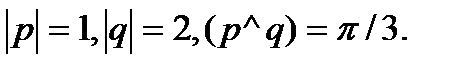
18. 
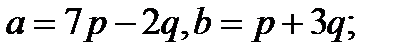
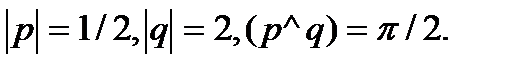
19. 
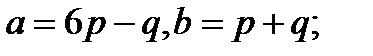
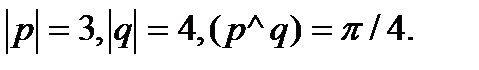
20. 
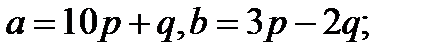
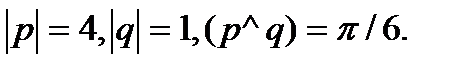
21. 
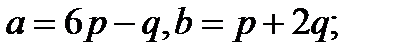
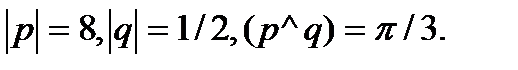
22. 
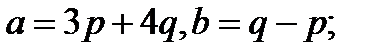
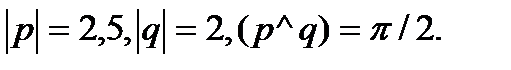
23. 
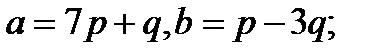
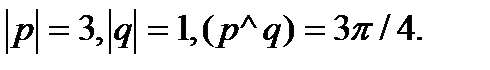
24. 
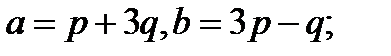
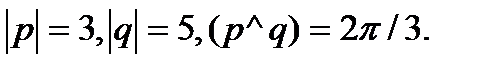
25. 
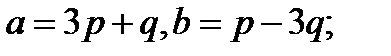
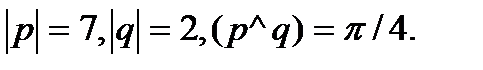
26. 
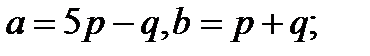
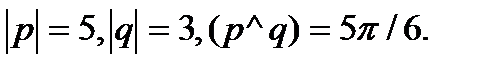
27. 
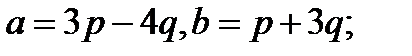
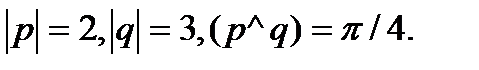
28. 
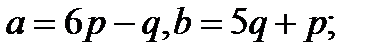
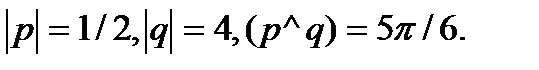
29. 
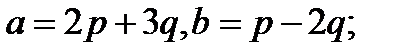
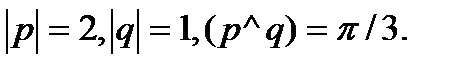
30. 
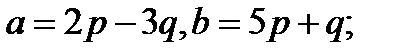
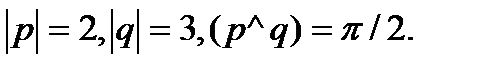
31. 
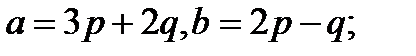
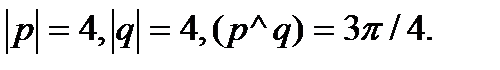
32. 
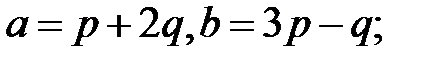
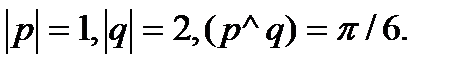
Задача 6.Компланарны ли векторы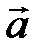 
, 
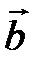и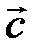 
.
1. 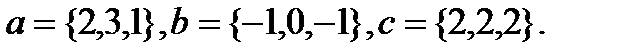 | 17.  |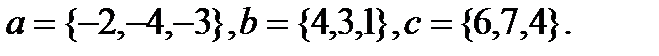
2. 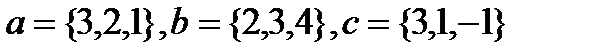 | 18.  |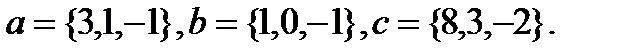
3. 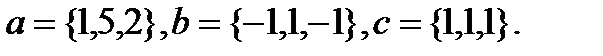 | 19.  |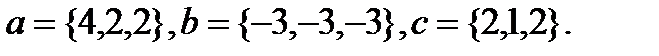
4. 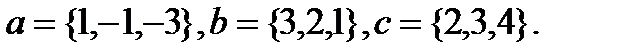 | 20.  |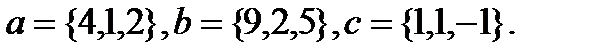
5. 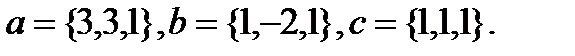 | 21.  |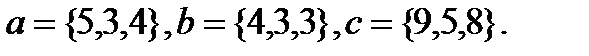
6. 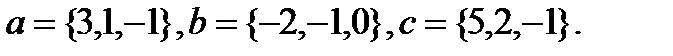 | 22.  |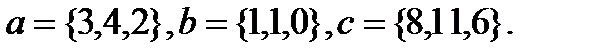
7. 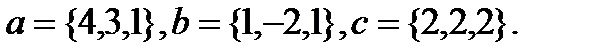 | 23.  |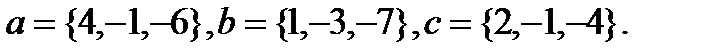
8. 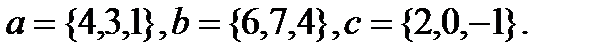 | 24.  |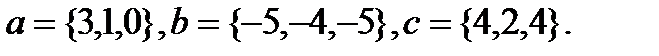
9. 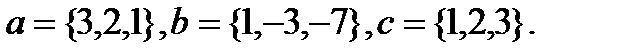 | 25.  |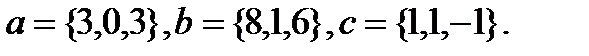
10. 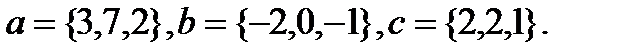 | 26.  |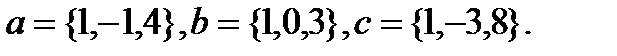
11. 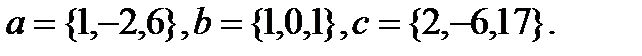 | 27.  |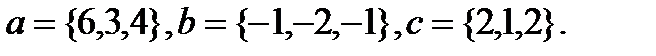
12. 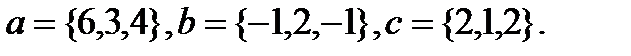 | 28.  |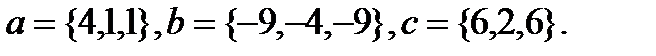
13. 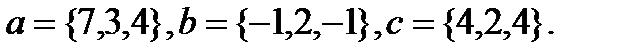 | 29.  |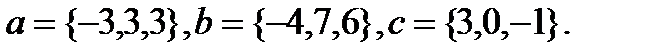
14. 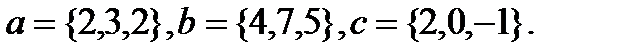 | 30.  |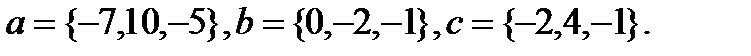
15. 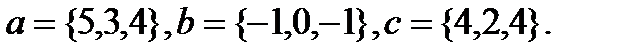 | 31.  |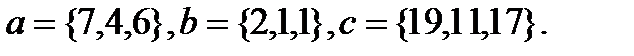
16. 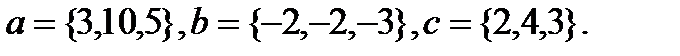 | 32. |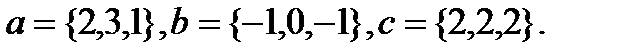
Задача 7. Найти угол между плоскостями.
1. 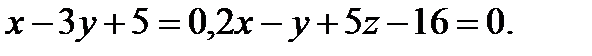 | 17.  |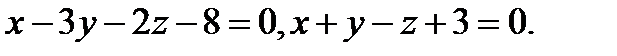
2. 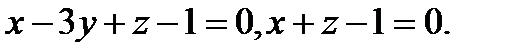 | 18.  |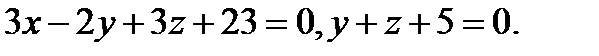
3. 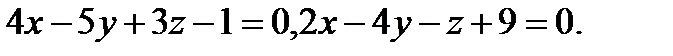 | 19.  |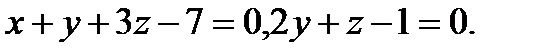
4. 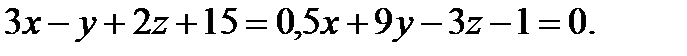 | 20.  |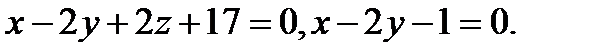
5. 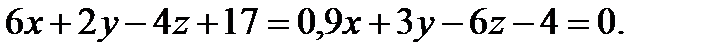 | 21.  |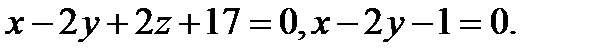
6. 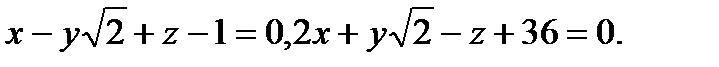 | 22.  |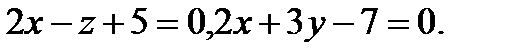
7. 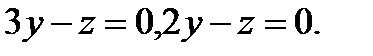 | 23.  |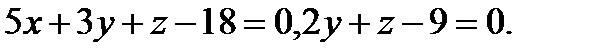
8. 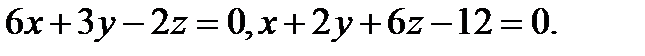 | 24.  |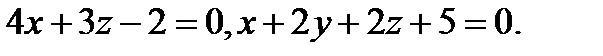
9. 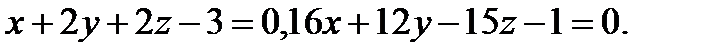 | 25.  |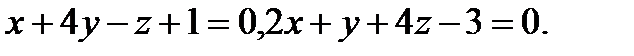
10. 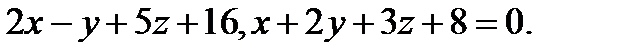 | 26.  |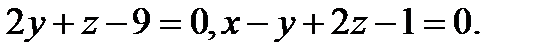
11. 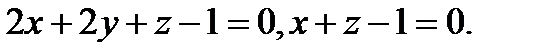 | 27.  |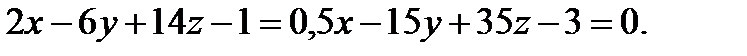
12. 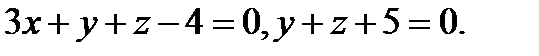 | 28.  |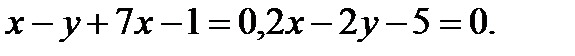
13. 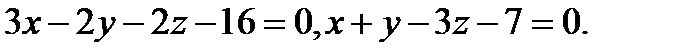 | 29.  |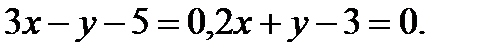
14. 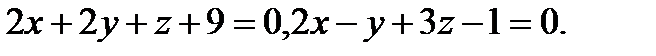 | 30.  |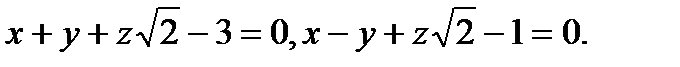
15. 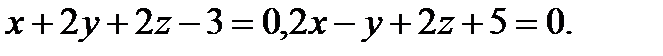 | 31.  |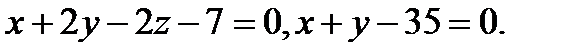
16. 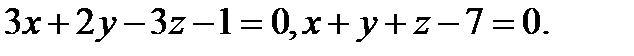 | 32. |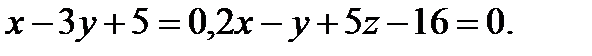
Задача 8. Написать канонические уравнения прямой, заданной двумя плоскостями.
1. 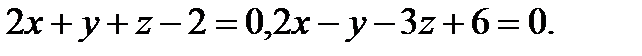 | 17.  |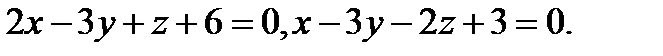
2. 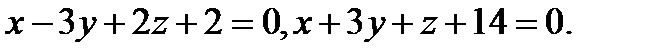 | 18.  |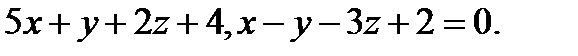
3. 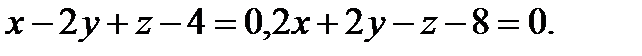 | 19.  |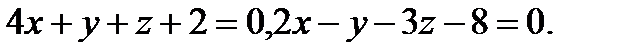
4. 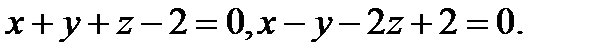 | 20.  |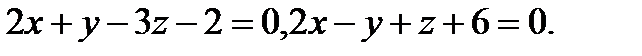
5. 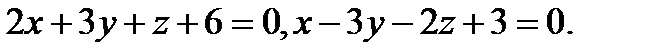 | 21.  |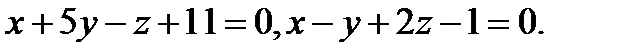
6. 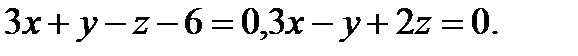 | 22.  |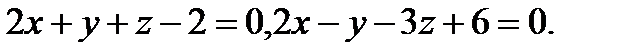
7. 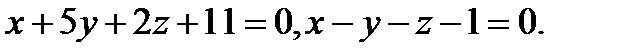 | 23.  |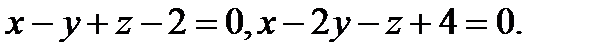
8. 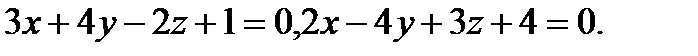 | 24.  |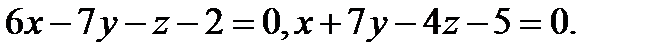
9. 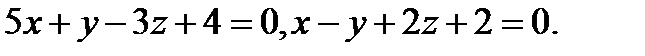 | 25.  |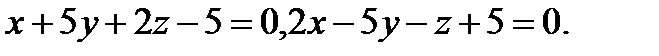
10. 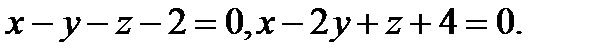 | 26.  |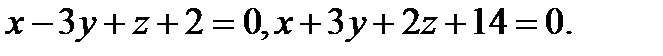
11. 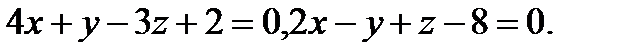 | 27.  |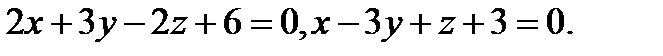
12. 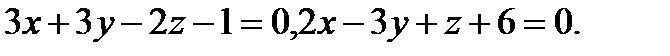 | 28.  |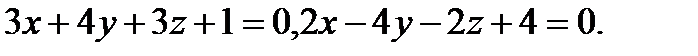
13. 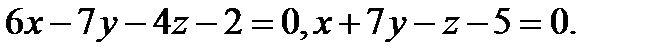 | 29.  |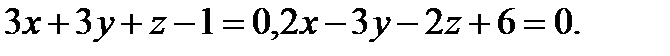
14. 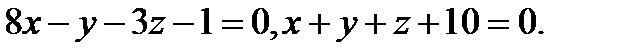 | 30.  |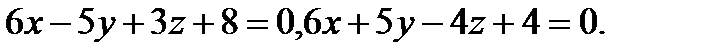
15. 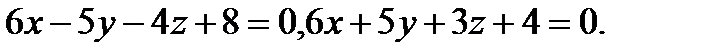 | 31.  |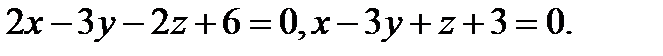
16. 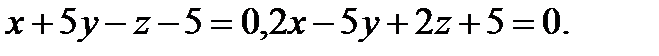 | 32. |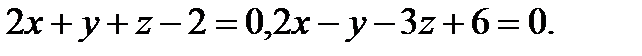
Задача 9. Найти точку пересечения прямой и плоскости.
1. 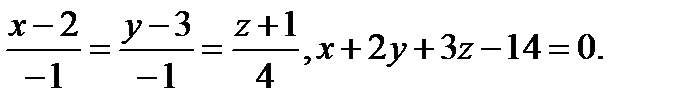 | 17.  |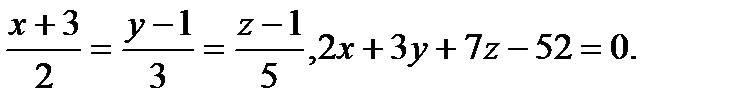
2. 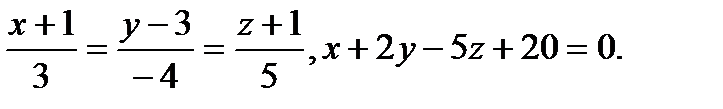 | 18.  |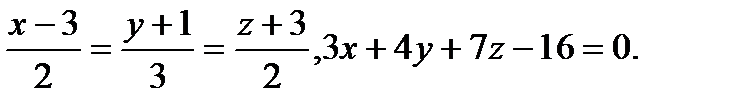
3. 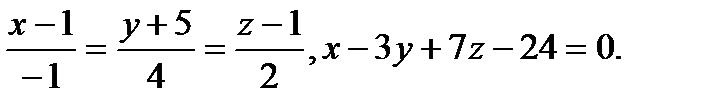 | 19.  |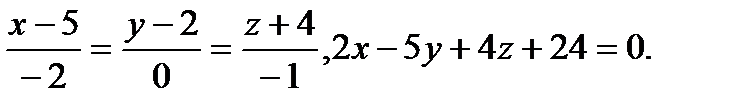
4. 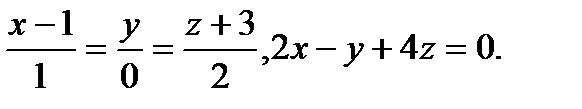 | 20.  |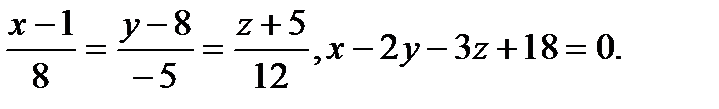
5. 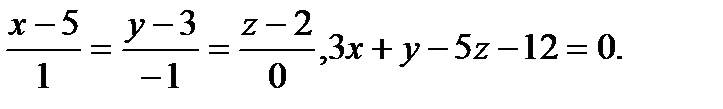 | 21.  |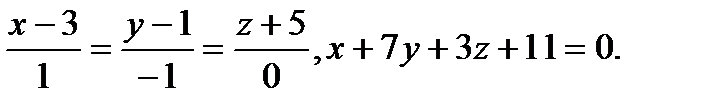
6. 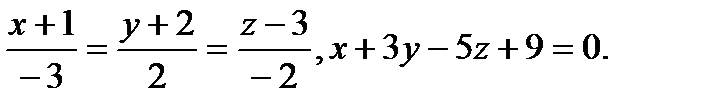 | 22.  |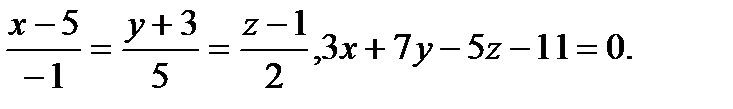
7. 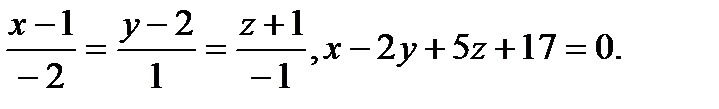 | 23.  |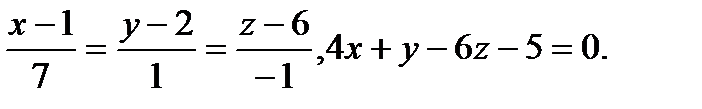
8. 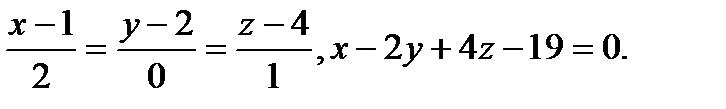 | 24.  |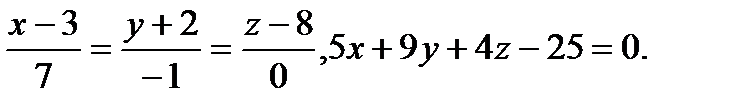
9. 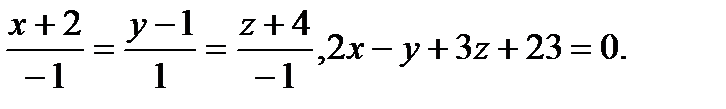 | 25.  |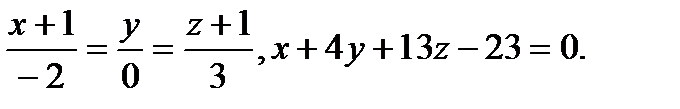
10. 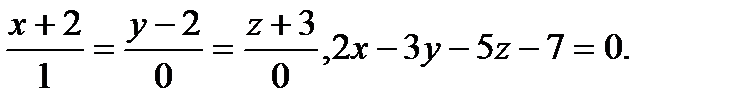 | 26.  |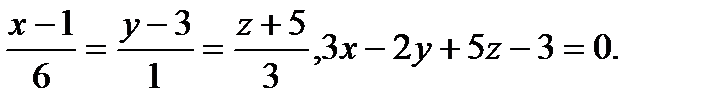
11. 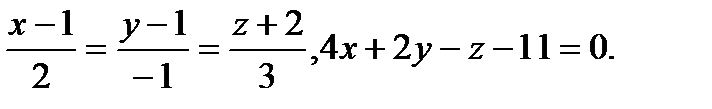 | 27.  |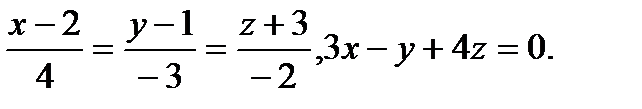
12. 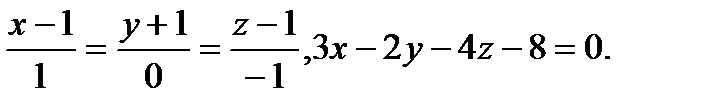 | 28.  |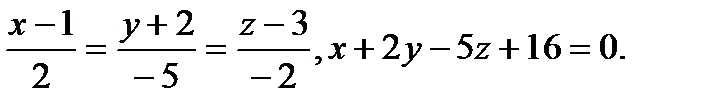
13. 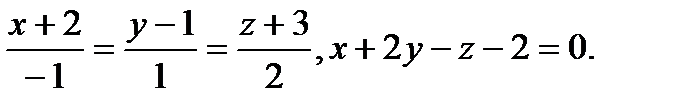 | 29.  |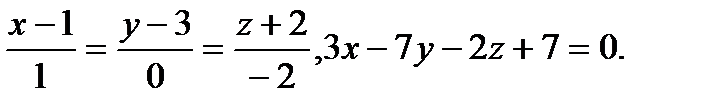
14. 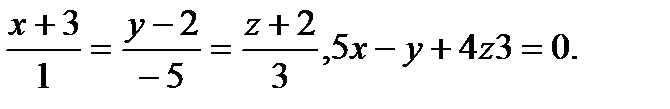 | 30.  |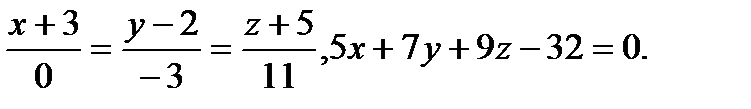
15. 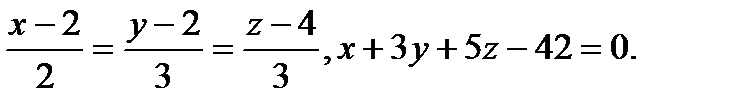 | 31.  |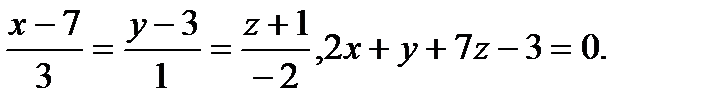
16. 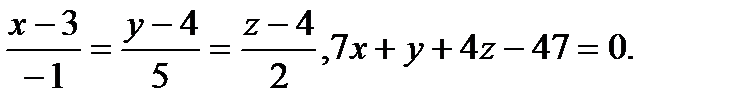 | 32. |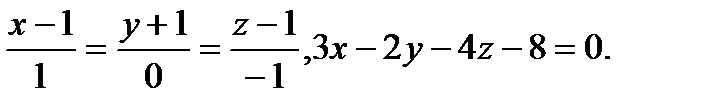
Тема: Функции одной переменной.
Задача 10.Вычислить пределы функций
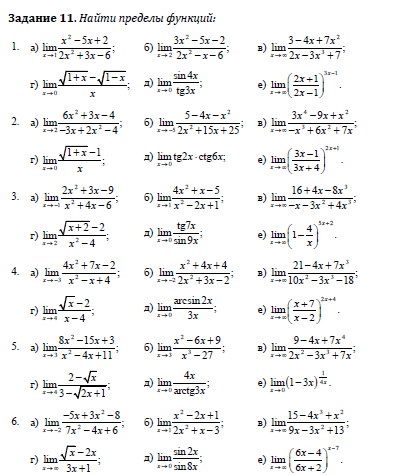
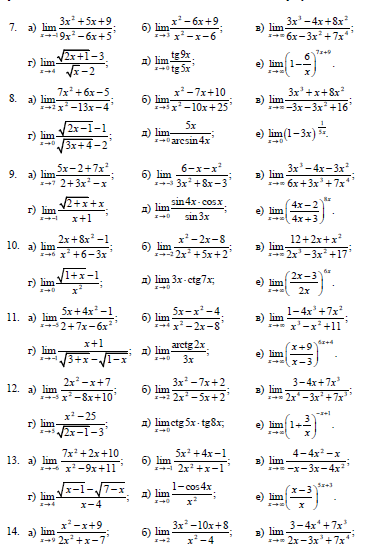
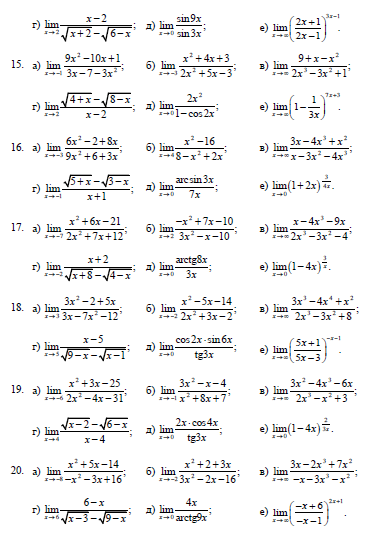
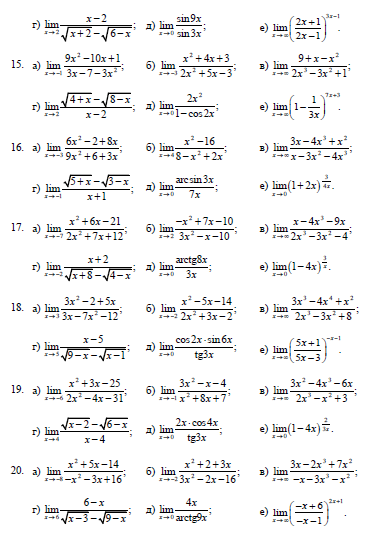
Задача 11.Найти производные функций
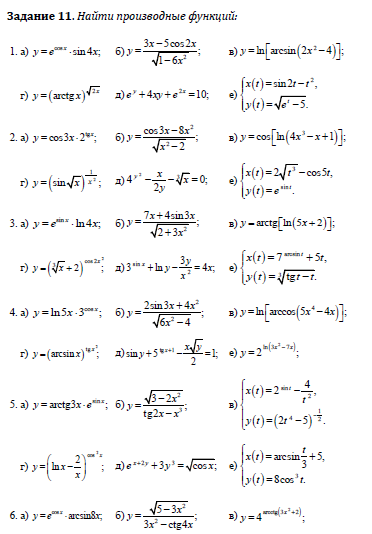
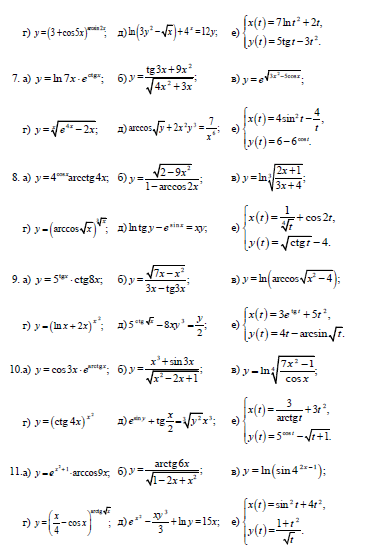
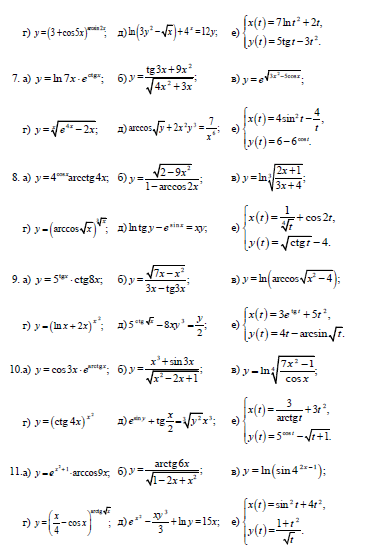
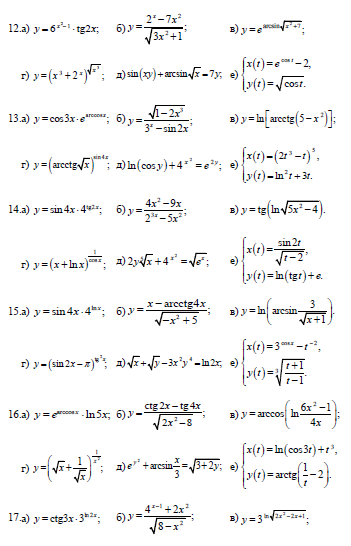
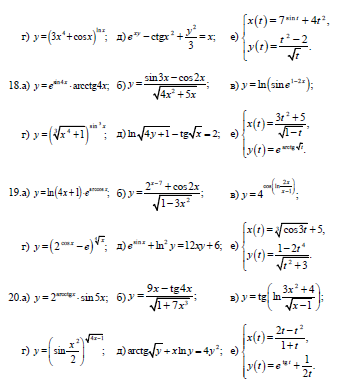
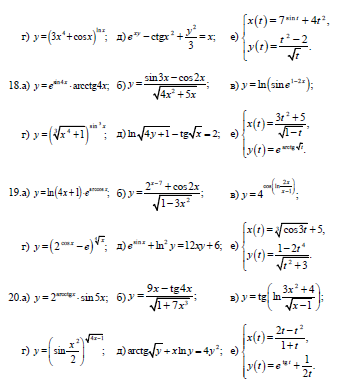
Задача 12.Найти производную функции в точке х0.
1. 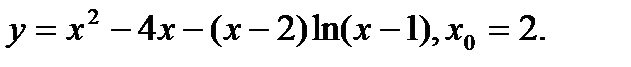 | 17.  |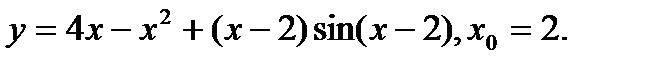
2. 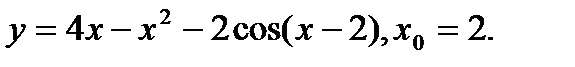 | 18.  |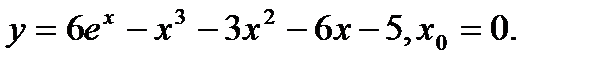
3. 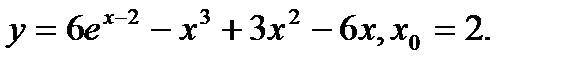 | 19.  |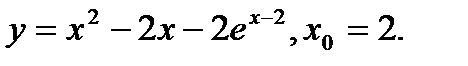
4. 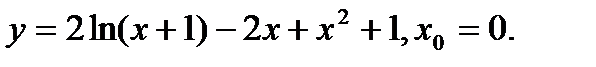 | 20.  |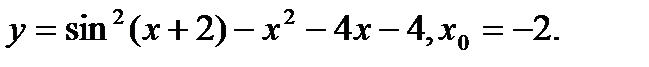
5. 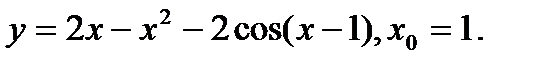 | 21.  |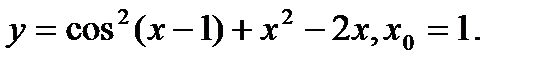
6. 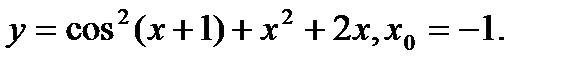 | 22.  |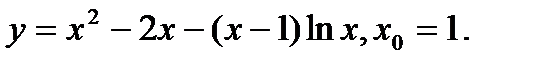
7. 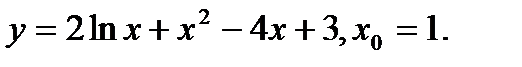 | 23.  |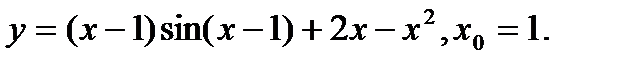
8. 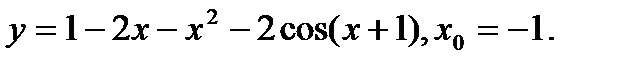 | 24.  |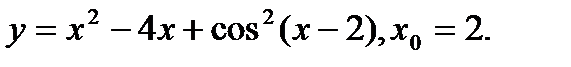
9. 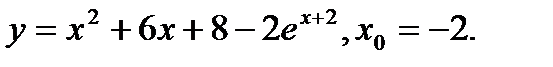 | 25.  |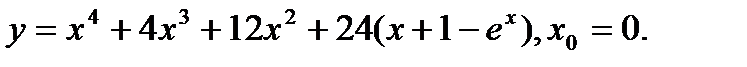
10. 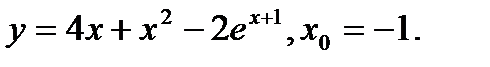 | 26.  |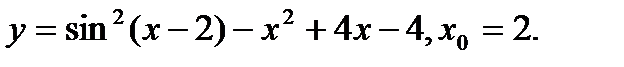
11. 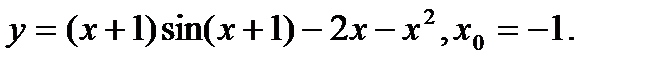 | 27.  |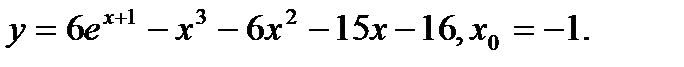
12. 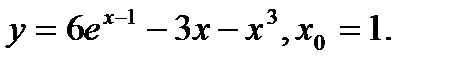 | 28.  |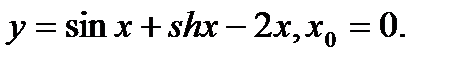
13. 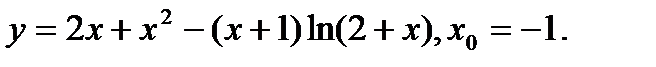 | 29.  |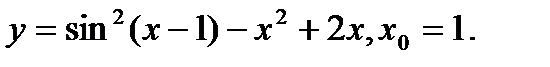
14. 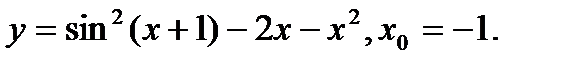 | 30.  |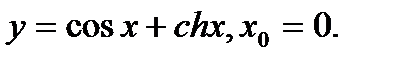
15. 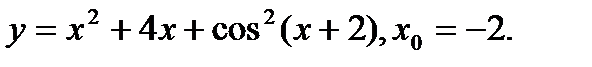 | 31.  |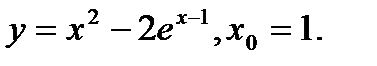
16. 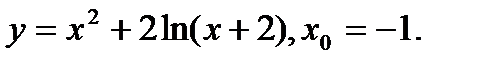 | 32. |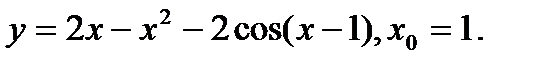
Задача 13.Провести полное исследование и построить графики функций.
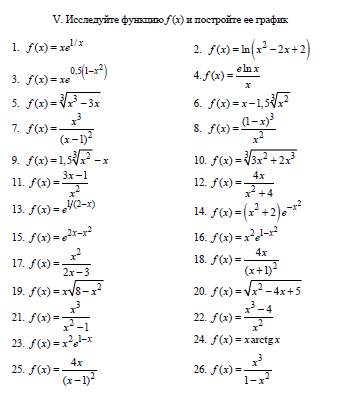
Литература:
1. Шипачев В.С. Высшая математика: Учеб. для вузов / В.С. Шипачев. – 6-е изд.; стер.-М.:Высш.шк., 2003г. – 479 с: ил. ISBN 5-06-003959-5
2. Шипачев В.С. Задачник по высшей математике: Учеб. для вузов / В.С. Шипачев. – 5-е изд.; стер.-М.:Высш.шк., 2005г. – 304 с: ил. ISBN 5-06-003575-1
Бермант А.Ф. Краткий курс математического анализа для втузов. М., 1973 г ., 720с с илл.
3. Элементы линейной алгебры: методические указания / Сост. Л.Н. Феофанова; Волгоград. Гос.тех.ун-т. – Волгоград, 1999 г. - 56с
4. Методические указания к типовой работе по теме «Линейная алгебра» / Сост. Л.А. Исаева., В.Ф. Исаев; Волгоград.гос.тех.ун-т – Волгоград, 1996г. – 20 с
5. Элементы линейной алгебры: стандартные задачи с основными приложениями теории: учебное пособие. / Феофанова Л. Н., Исаева Л. А., Исаев В. Ф. / ВолгГТУ – Волгоград, 2009. – 88 с.
6. Начала аналитической геометрии : учеб. пособие / Симонова И. Э., Тарасова И. А., Симонов Б. В., Ермакова А. А.; ВолгГТУ. - Волгоград: ВолгГТУ, 2010. - 48 с. : 1 электрон. опт. диск (CD.R)
Примеры решения некоторых задач
Задача 1. Решить систему линейных уравнений методом Крамера, с помощью обратной матрицы и методом Жордана-Гаусса.
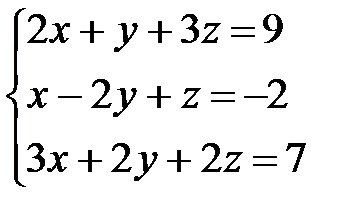
Решение:
Решение системы методом Крамера.
Найдем главный и вспомогательный определители системы:
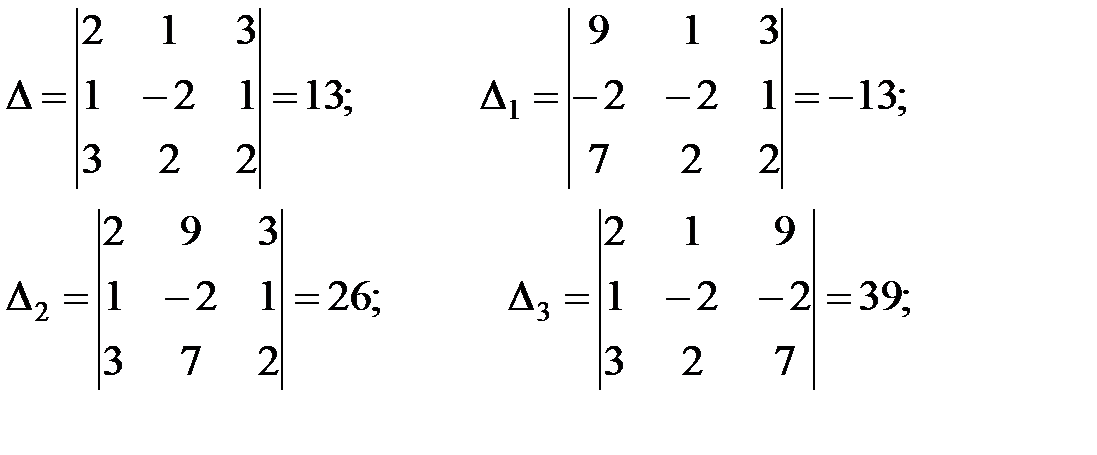
Так как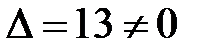 
, то система имеет единственное решение:
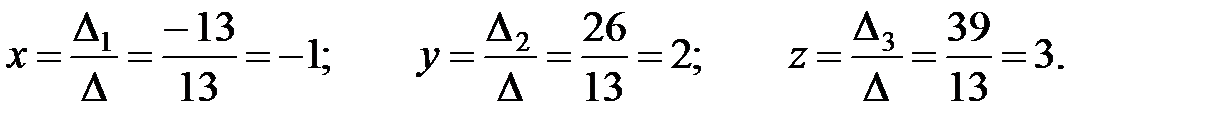
Решение системы с помощью обратной матрицы.
Заданную систему запишем в матричной форме АХ=В, где
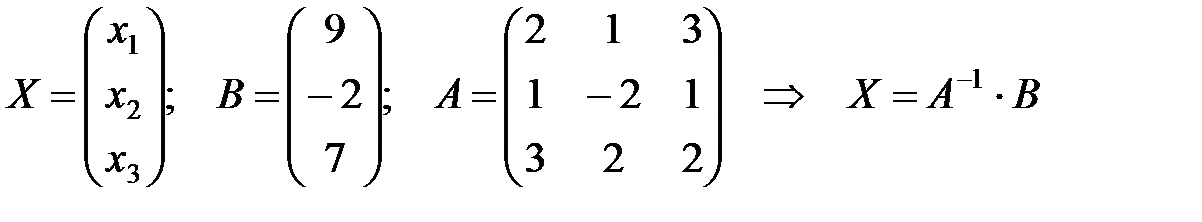
Матрица А системы неособенная, так как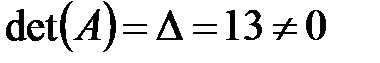 
, значит, существует обратная матрица 
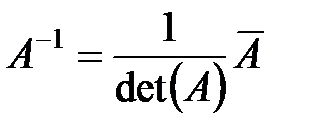, где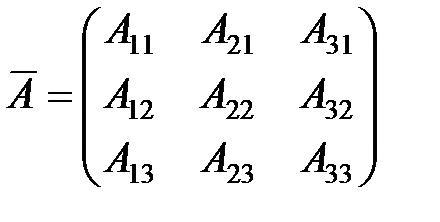 
.
Вычислим алгебраические дополнения Aij:
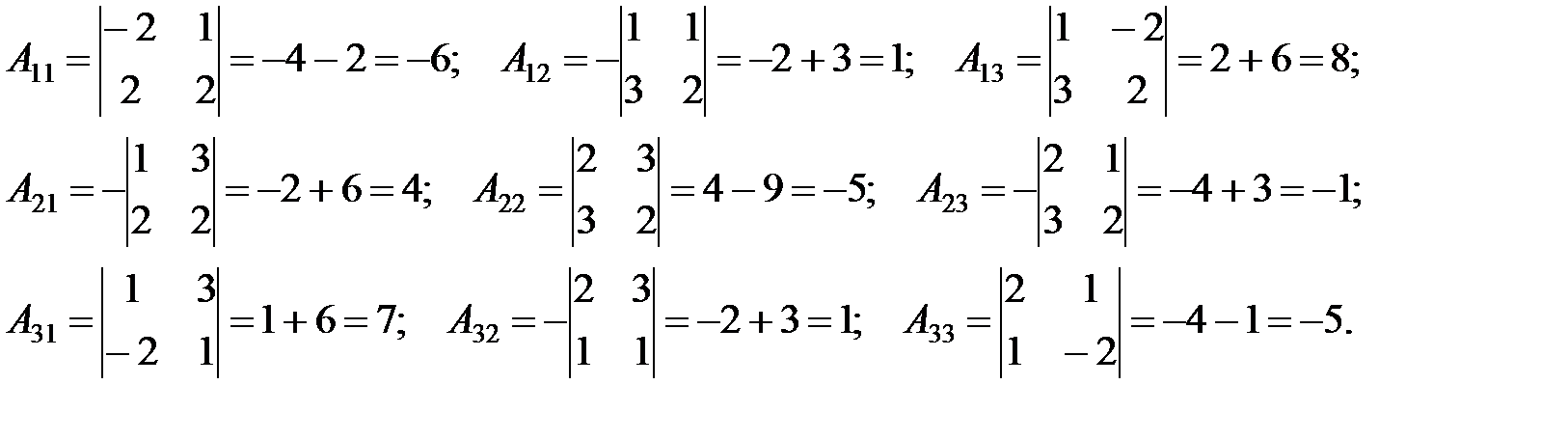
Затем находим обратную матрицу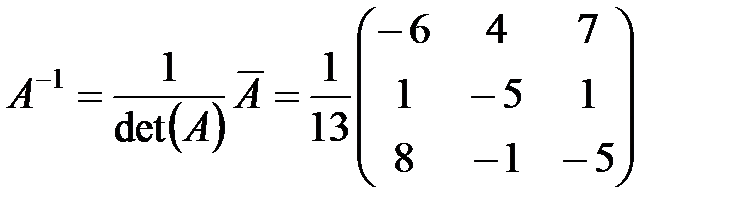 
Искомая матрица
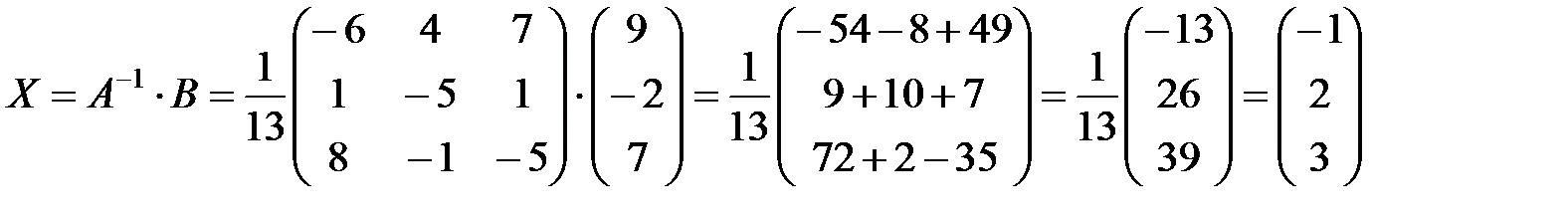
Из условия равенства матриц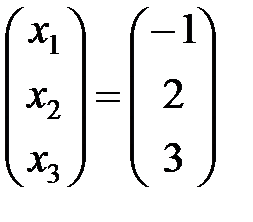 
получим решение данной системы уравнений:
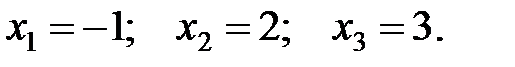
Решение системы методом Жордана-Гаусса.
Выпишем расширенную матрицу и элементарными преобразованиями над строками приведем ее к диагональному виду:
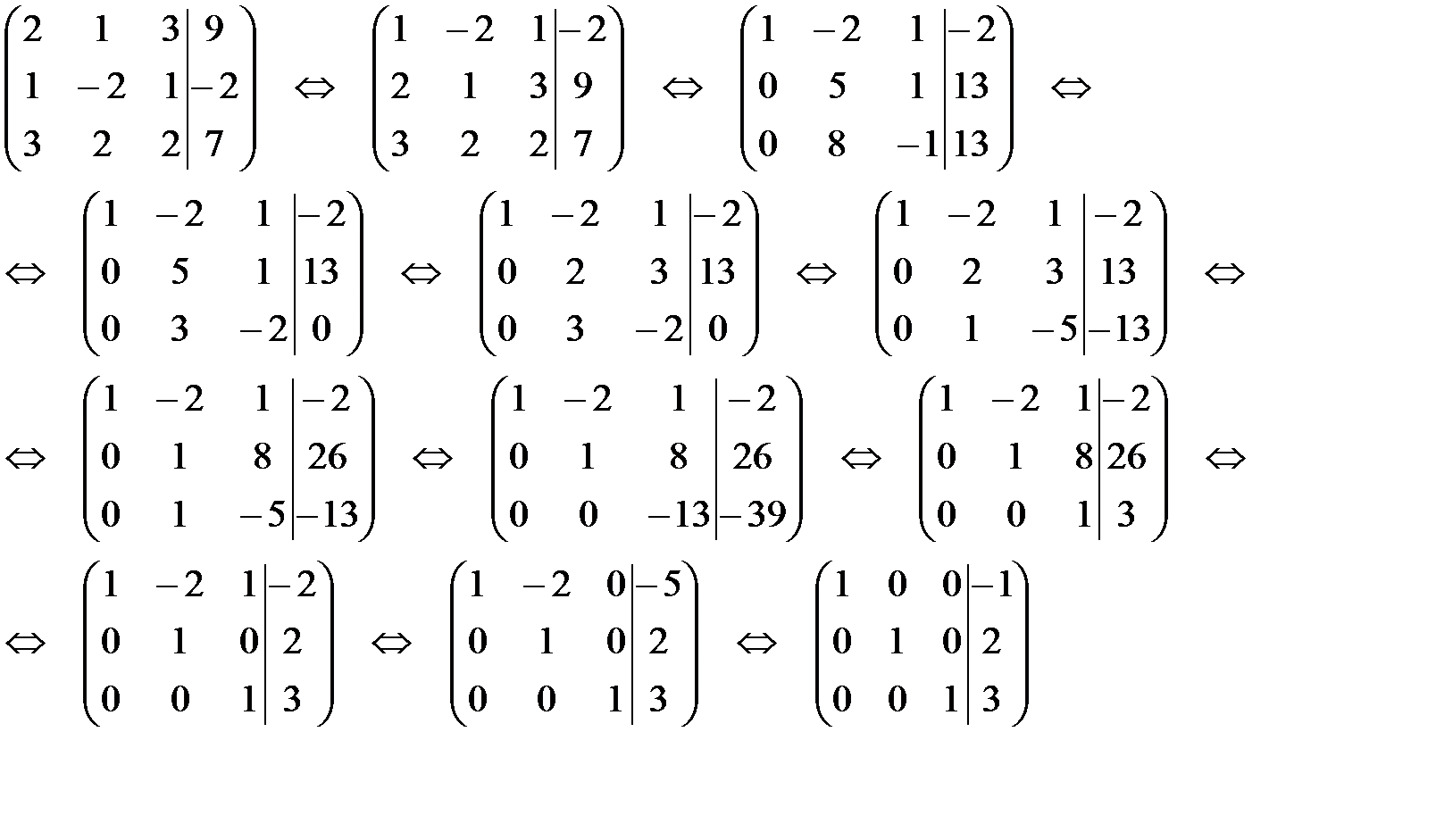
Ответ: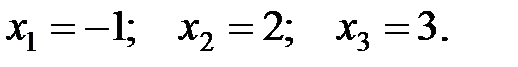 
Задача 2.Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) найти все корни уравнения .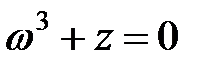
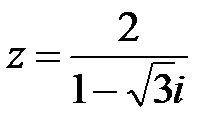
Решение:
1) Запись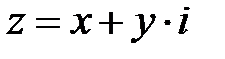 
называется алгебраической формой комплексного числа, где х – вещественная часть, y – мнимая часть.
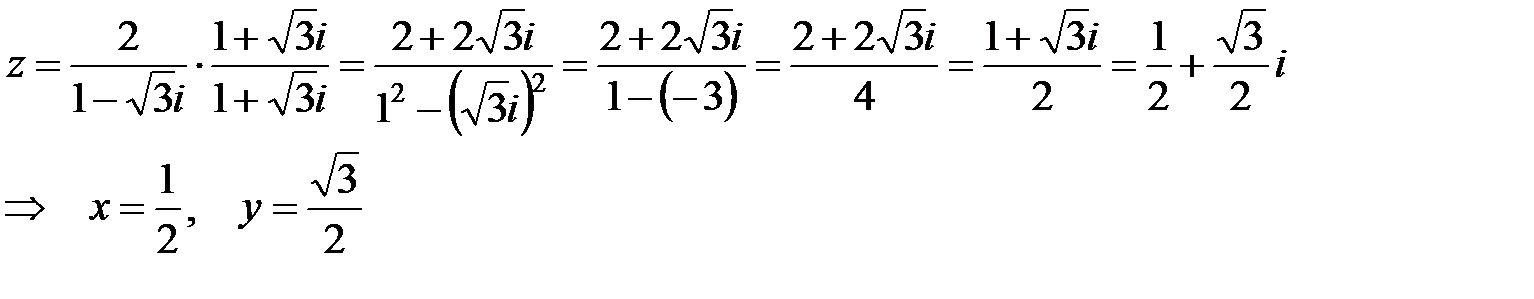
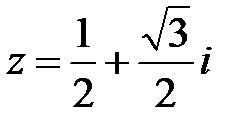- алгебраическая форма.
Запись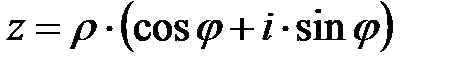 
называется тригонометрической формой комплексного числа, где 
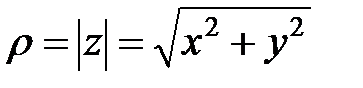- называется модулем, а число 
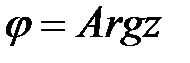- аргументом.
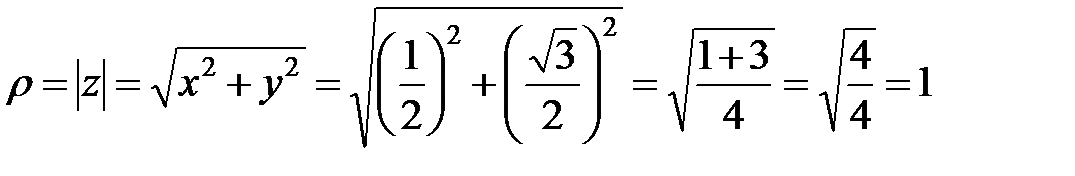
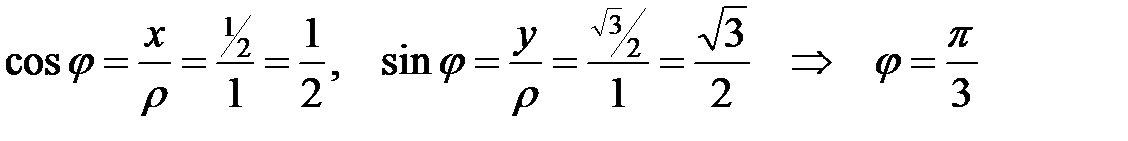
Следовательно,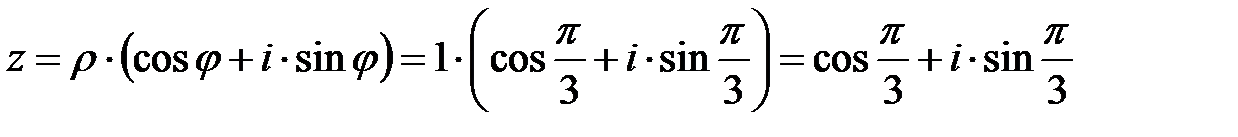 
2) найдем все корни уравнения .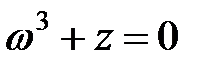
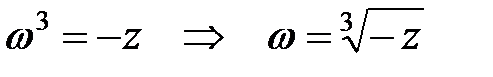
Обозначим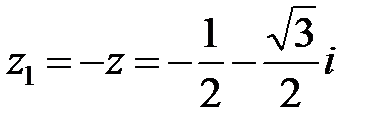 
, тогда
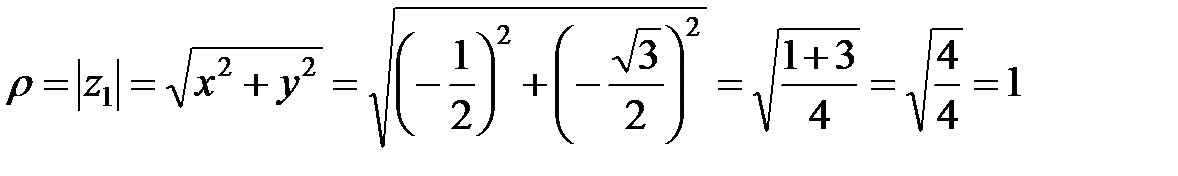
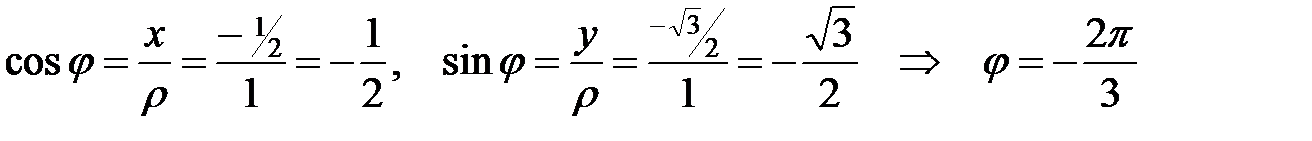
Таким образом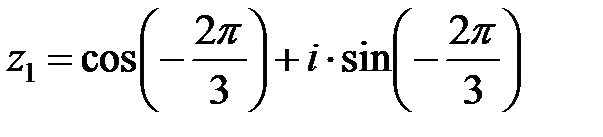 
.
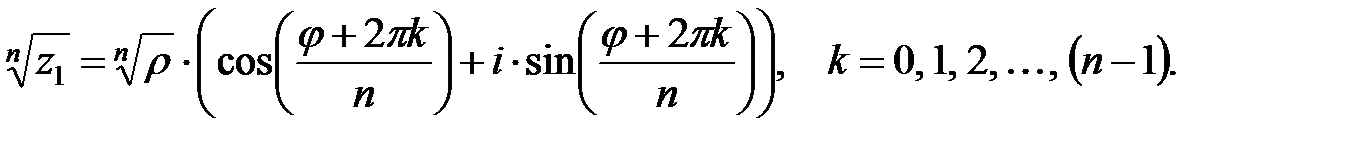
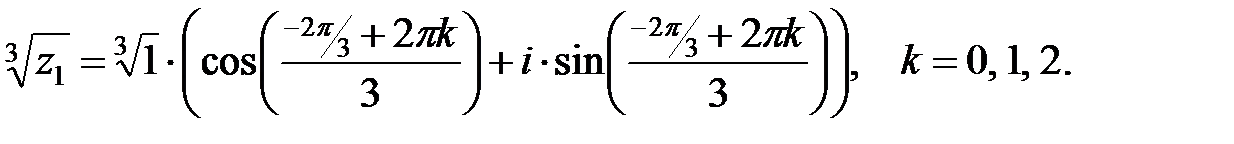
При k=0:
,
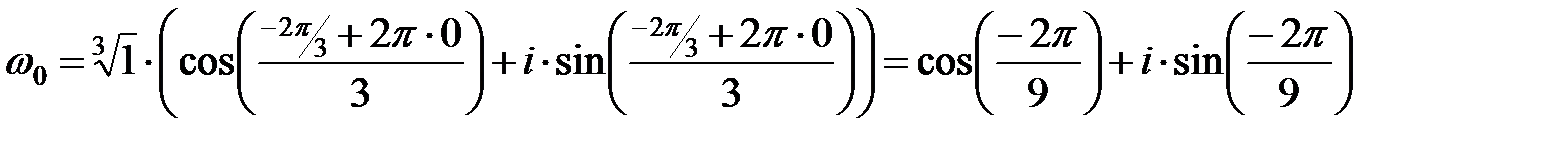При k=1:
,
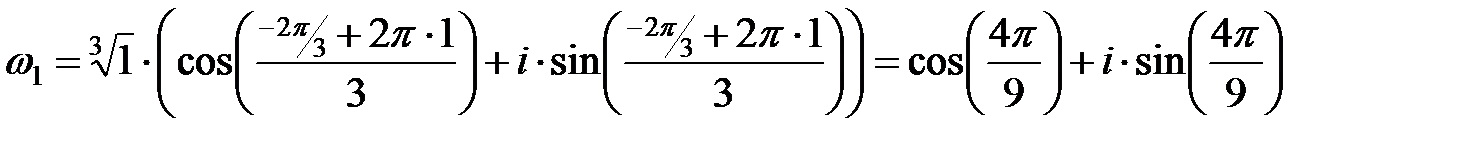При k=2 :
.
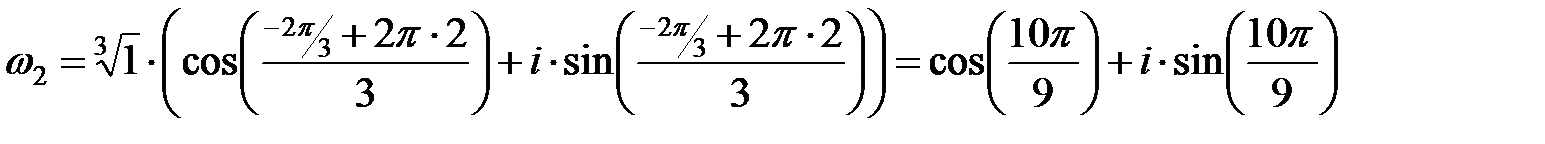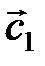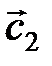Задача 3.Коллинеарны ли векторы и , построенные по векторам 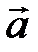и ?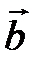
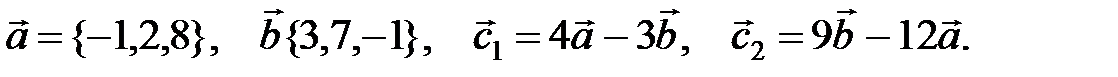
Решение:
Найдем координаты векторов 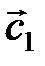и .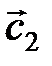
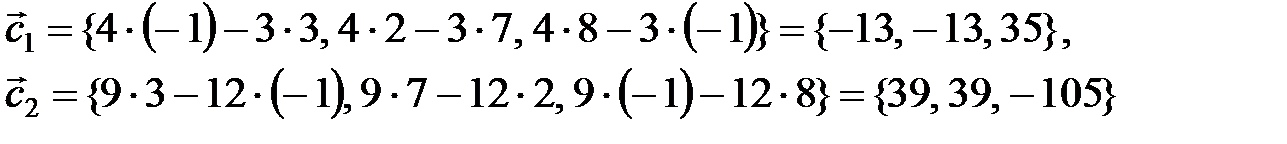
Проверим условие коллинеарности векторов.
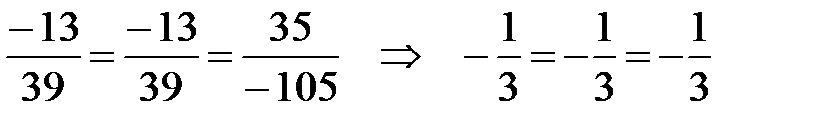
Так как условие выполняется, то векторы 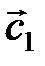и 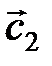коллинеарны.
Ответ:коллинеарны.
Задача 4. Найти косинус угла между векторами 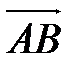и .
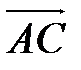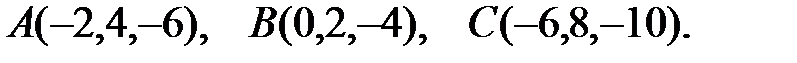
Решение:
Найдем координаты векторов 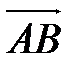и .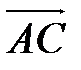
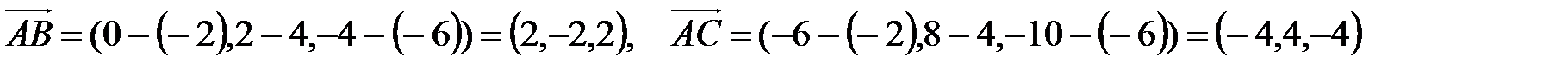
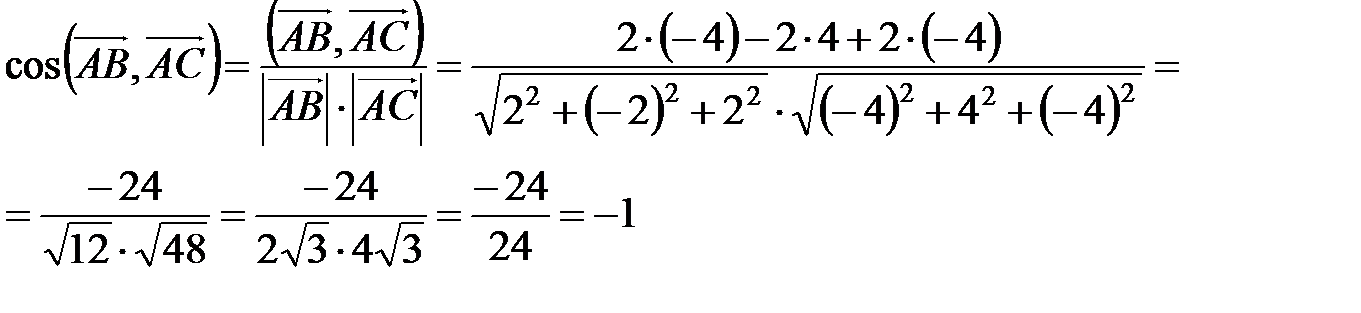
Ответ:-1.
Задача 5.Вычислить площадь параллелограмма, построенного на векторах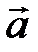 
и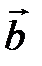 
.
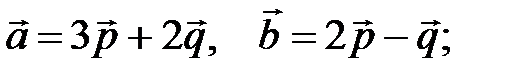
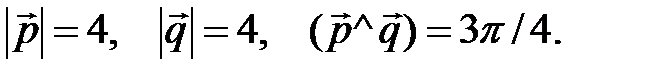
Решение:
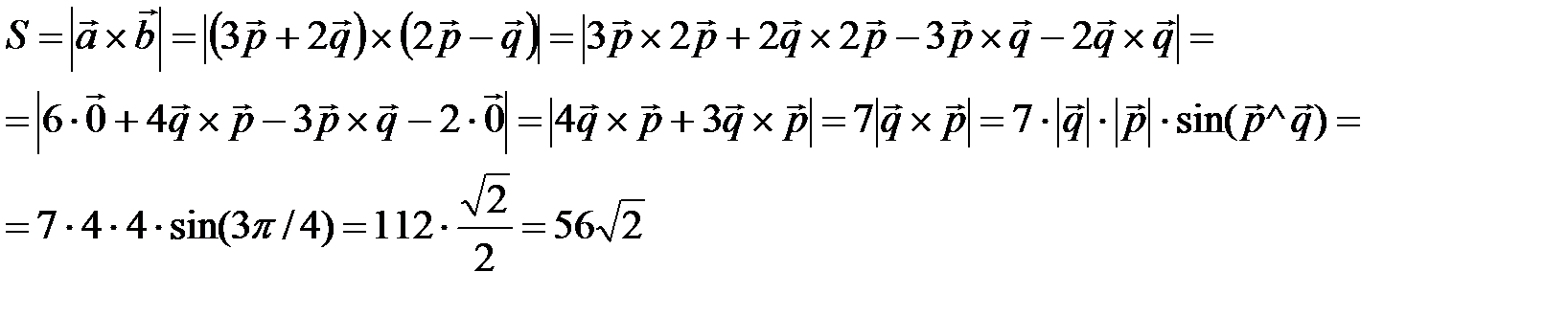
Ответ: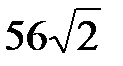 
.
Задача 6.Компланарны ли векторы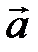 
, 
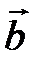и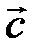 
.
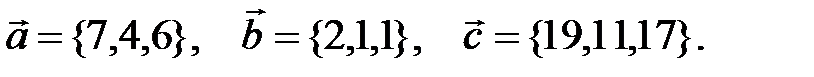
Решение:
Вычислим смешанное произведение векторов 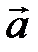, 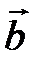и .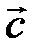
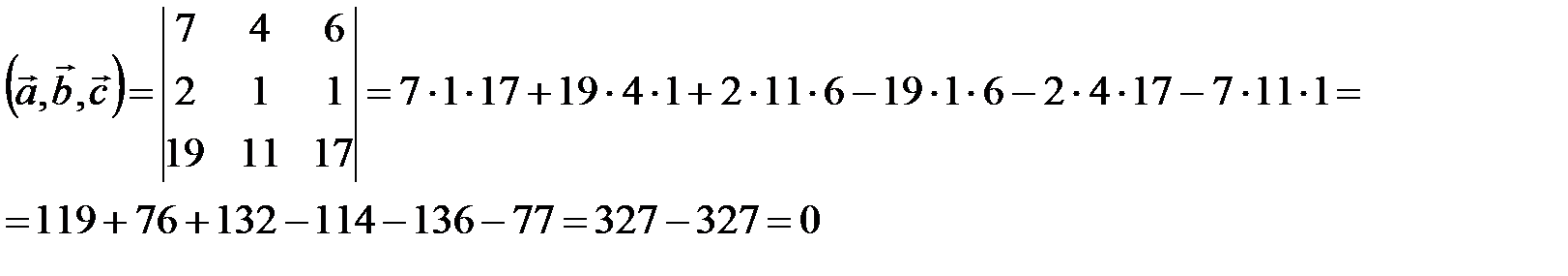
Так как смешанное произведение векторов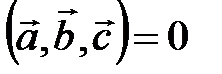 
, то векторы 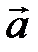, 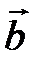и 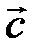компланарны.
Ответ:компланарны.
Задача 7. Найти угол между плоскостями.
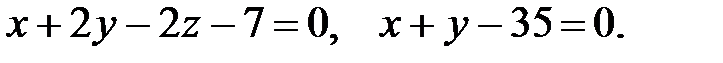
Решение:
Нормальные векторы плоскостей имеют координаты: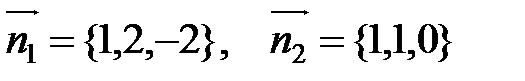 
.
Угол между плоскостями равен углу между их нормальными векторами.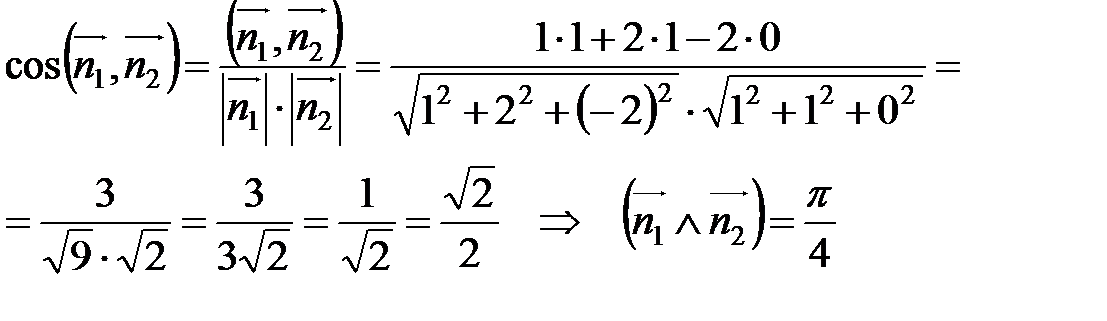 
Ответ: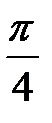 
.
Задача 8. Написать канонические уравнения прямой, заданной двумя плоскостями.
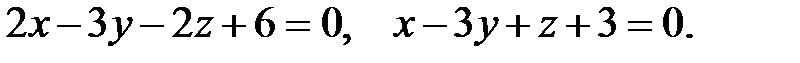
Решение:
Нормальные векторы плоскостей имеют координаты: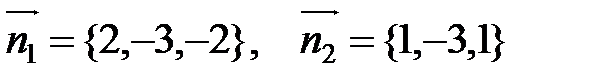 
.
Определим направляющий вектор прямой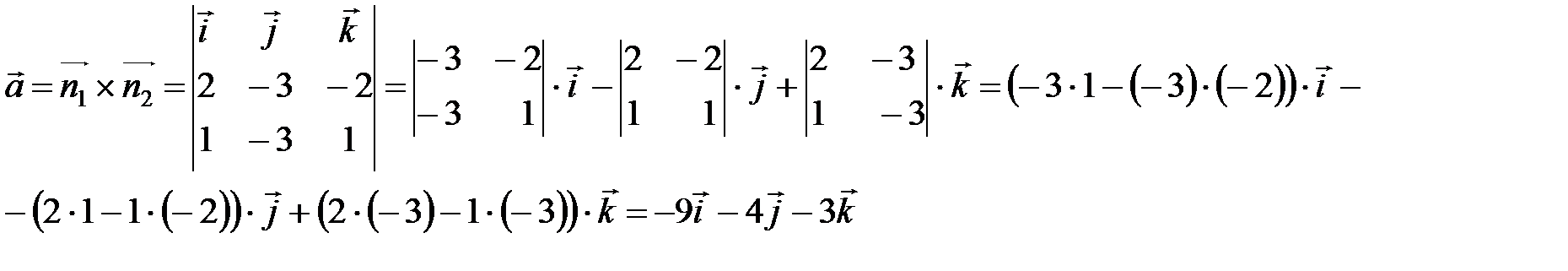 
Найдем координаты точки М, принадлежащей прямой. Для этого решим систему уравнений
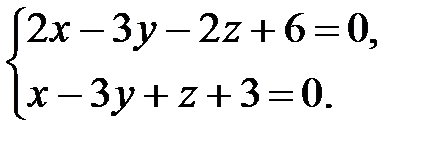
Положим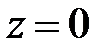 
, тогда система примет вид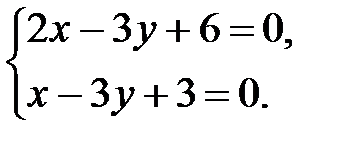 
Вычитая из первого уравнения второе, получим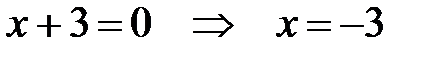 
Подставляя найденное x во второе уравнение, найдем y: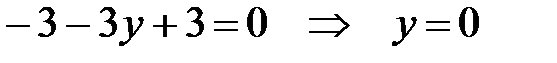 
Таким образом, точка М имеет координаты (-3, 0, 0).
Запишем канонические уравнения искомой прямой:
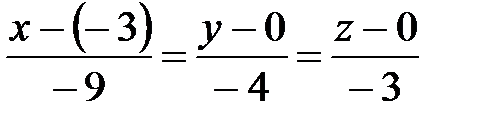или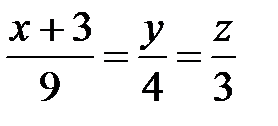 
Ответ: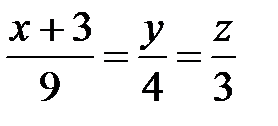 
.
Задача 9. Найти точку пересечения прямой и плоскости.
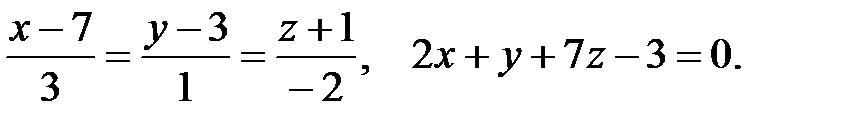
Решение:
Так как точка принадлежит и прямой, и плоскости, то ее координаты можно найти, решив систему уравнений: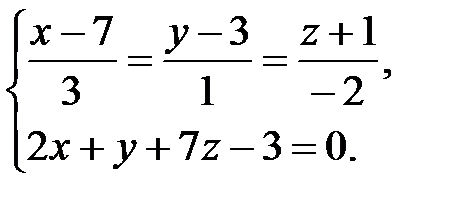 
Запишем уравнение прямой в параметрическом виде и подставим в уравнение плоскости
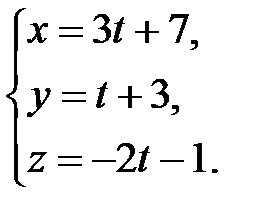
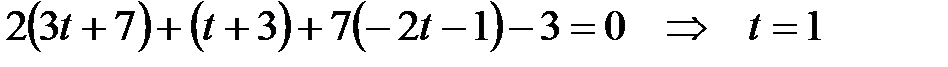
Подставляя найденное значение t в параметрические уравнения прямой, найдем координаты искомой точки:
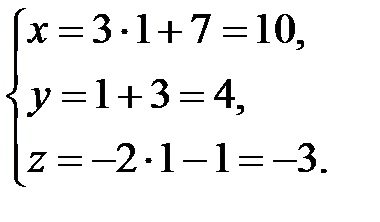
Ответ: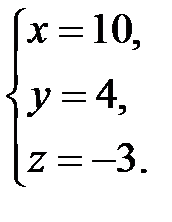 
Задача 10.Найти производную функции в точке х0 :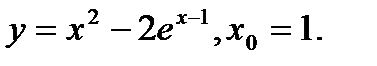
Решение:
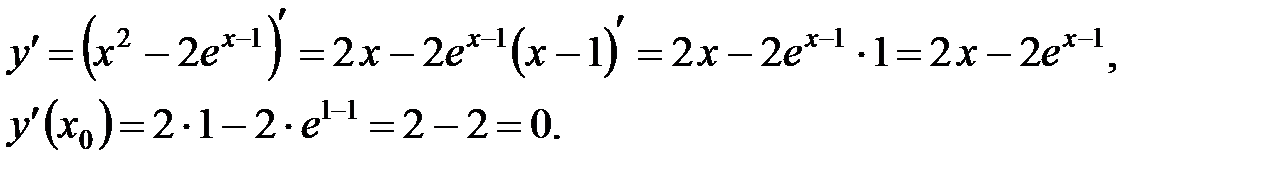
Ответ:0.
Задача 11.Найти производную функции: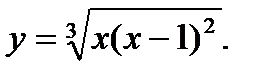 
Решение:
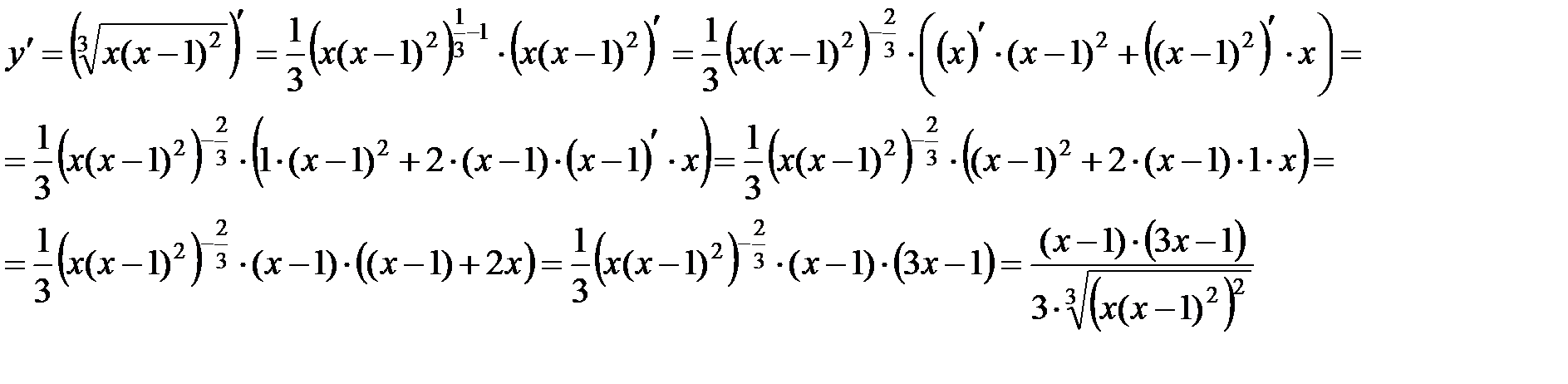
Ответ: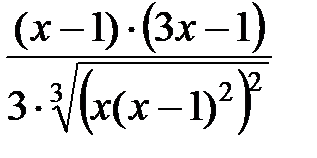 
.
Задача 12.Найти производную функции: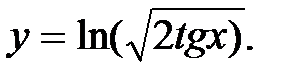 
Решение:
Учитывая свойства логарифма: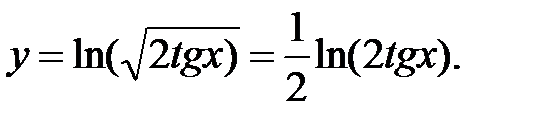 
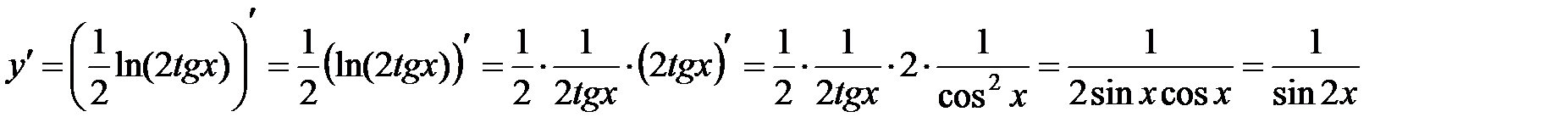
Ответ: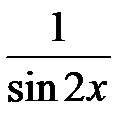 
.