Векторная алгебра и аналитическая геометрия
Математика
Программа и контрольные задания
для студентов I и II курсов заочной формы обучения
всех специальностей
Екатеринбург
УДК 51.(075.8)
Составители В.Б.Грахов, Р.М.Минькова, В.Б.Соловьянов
Научный редактор доц., канд. техн. наук В.А.Нырко
Математика: программа и контрольные задания / В.Б.Грахов, М.Минькова, В.Б.Соловьянов. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 40 с.
Приведённый в работе материал и задания к нему распределены по семестрам, в соответствии со специальностями и учебными графиками, утверждёнными в УГТУ-УПИ. Предназначена для студентов I и II курсов заочной формы обучения всех специальностей.
Библиогр.: 21 назв. Табл. 6.
Подготовлено кафедрой «Вычислительные методы и уравнения математической физики».
© ГОУ ВПО «Уральский государственный
технический университет-УПИ», 2005
Введение
В настоящих методических указаниях приведена программа и контрольные задания по математике для студентов заочной формы обучения УГТУ-УПИ. В процессе изучения курса математики студент должен выполнить в каждом семестре 2 контрольные работы. Номер варианта определяется по последней цифре номера студенческого билета или зачётной книжки. Так, например, если этот номер заканчивается цифрой 5, то в контрольной работе № 1 нужно решить задачи 5, 15, 25, 35.
При выполнении контрольных работ нужно придерживаться следующих правил.
1. Каждую контрольную работу следует выполнять в отдельной тетради,
оставляя поля для замечаний рецензента.
2. На обложке тетради необходимо указать: а) свою фамилию и инициалы;
б) специальность обучения; в) номер зачётной книжки; г) название дисциплины; д) номер контрольной работы.
3. В контрольную работу должны быть включены все задачи, указанные в задании, и в строгом соответствии с номером своего варианта.
4. Решения задач в каждой контрольной работе следует располагать обязательно в порядке номеров, указанных в задании. Перед решением каждой задачи необходимо выписать полностью её условие.
5. Решения задач должны содержать подробные пояснения и необходимые чертежи.
6. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом замечания и недочёты, а также выполнить все его рекомендации. Все исправления нужно записывать в этой же тетради после всех решённых задач контрольной работы. Вносить исправления в тексты решения задач после рецензирования запрещается. Незачтённую контрольную работу с последующими соответствующими исправлениями следует направить на повторную рецензию.
7. Контрольные работы в каждом семестре должны быть представлены для рецензирования не позднее чем за2 недели до начала экзаменационной сессии. Рецензирование контрольных работ, присланных позже указанного срока, переносится на начало следующего семестра.
Прорецензированные и зачтённые контрольные работы студент должен предъявлять экзаменатору перед сдачей зачёта или экзамена.
Во время сдачи зачёта или экзамена студент должен показать понимание основных теоретических и практических вопросов программы и умение применять их в решении задач и примеров. Определения, теоремы и правила должны формулироваться точно и с пониманием существа вопросов.
Во время экзаменационных сессий для студентов-заочников организуются обзорные лекции и практические занятия по программам предыдущего семестра, а также установочные лекции по программам следующего семестра.
В межсессионный период по субботам проводятся просмотры лекций по телевидению, а каждую чётную субботу – консультации, приём зачётов и экзаменов. Информация о датах и времени их проведения вывешивается на кафедральном стенде после окончания экзаменационной сессии.
 I семестр
I семестр
Программа
Векторная алгебра и аналитическая геометрия
1. Определители 2-го и 3-го порядков.
2. Векторы в 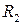 и
и 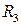 : линейные операции, базис, координаты, условие коллинеарности. Проекция вектора на ось.
: линейные операции, базис, координаты, условие коллинеарности. Проекция вектора на ось.
3. Скалярное, смешанное и векторное произведение векторов в 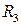 : определения, свойства, формулы вычисления через координаты векторов в ортонормированном базисе.
: определения, свойства, формулы вычисления через координаты векторов в ортонормированном базисе.
4. Уравнение плоскости в 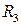 с заданным нормальным вектором. Условия параллельности и перпендикулярности двух плоскостей. Отыскание угла между двумя плоскостями, расстояния от точки до плоскости.
с заданным нормальным вектором. Условия параллельности и перпендикулярности двух плоскостей. Отыскание угла между двумя плоскостями, расстояния от точки до плоскости.
5. Уравнение прямой на плоскости и в пространстве: канонические уравнения, параметрические уравнения; общее уравнение прямой в пространстве. Условия параллельности и перпендикулярности двух прямых, прямой и плоскости. Отыскание угла между двумя прямыми на плоскости, угла между прямой и плоскостью.
6. Кривые второго порядка: эллипс, гипербола, парабола и их канонические уравнения. Поверхности второго порядка и их построение.
7. Комплексные числа. Модуль и аргумент комплексного числа. Алгебраическая, тригонометрическая и показательная форма записи комплексного числа. Операции над комплексными числами: сложение, вычитание, деление, возведение в степень, извлечение корня.
Введение в математический анализ
1. Определение предела функции в точке, в бесконечности. Предел последовательности как частный случай предела функции. Односторонние пределы функции. Основные теоремы о пределе функции.
2. Бесконечно малые и бесконечно большие функции и их свойства; связь бесконечно больших функций с бесконечно малыми. Сравнение бесконечно малых.
3. Отыскание предела отношения двух многочленов при 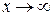 . Первый и второй замечательный пределы.
. Первый и второй замечательный пределы.
4. Функции, непрерывные в точке, и их свойства. Точки разрыва функции и их классификация.
5. Функции, непрерывные на отрезке, и их свойства.
