Нахождение пути, перемещения и радиус-вектора по скорости

Решение обратной задачи, а именно, нахождение перемещения , пути s₁₂ и радиус-вектора по известной скорости требует применения математической задачи, обратной взятию производной, то есть интегрирования:

. .

Постоянная С находится из начальных условий.

Ускорение.

Ускорение говорит о том, как быстро меняется скорость. Мгновенное (полное) ускорение:

Скорость величина векторная, направленная по касательной к траектории. У нее может меняться как модуль, так и направление. Если представим вектор скорости в виде произведения модуля и единичного вектора (направленного по касательной к траектории): , то при взятии производной получим два слагаемых:

,

каждое из которых имеет свой физический смысл.

Тангенциальное ускорение

показывает, как быстро меняется модуль скорости. Модуль тангенциального ускорения:

.

Нормальное ускорение

показывает, как быстро меняется направление скорости. Модуль нормального ускорения может быть сосчитан по формуле

,

где R - радиус кривизны траектории. Направлено нормальное ускорение по нормали (то есть перпендикулярно) к траектории:

,

здесь - единичный вектор нормали.

Полное ускорение представляет собой сумму двух ускорений. Тангенциальное и нормальное ускорения взаимно перпендикулярны и поэтому модуль полного ускорения a связан с их модулями формулой:

Итак, зная можно найти Зная можно найти и , а затем и радиус кривизны траектории

Рис.3. Полное нормальное и тангенциальное ускорения.

Вращательное движение

Рис.4. Вращение точек твёрдого тела. Рис.5. Вращение. Вектора и

При вращении твердого тела две разные точки его (на расстоянии Rа и Rв от центра) за время 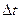пройдут разные пути s1 и s2. Но так как тело абсолютно твердое радиусы Rа и Rв повернутся на одинаковый угол φ. Потому угол можно рассматривать, как общую характеристику при вращении твёрдого тела. За один и тот же промежуток времени: за время 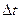Таким образом угол поворота будет являться характеристикой вращательного движения для всего тела в целом. Скорость вращения (угловая скорость) может быть найдена с помощью операции взятия производной. . Для учета направления вращения с угловой скоростью связывают вектор, направленный вдоль оси вращения так, чтобы из конца вектора направление движения было видно против часовой стрелки. Вектор имеет такое же направление.

Угловое ускорение и угол поворота связаны с угловой скоростью соотношениями аналогичным тем, что используются при описании поступательного движения: , .

Аналогия записи поступательного и вращательного движения и взаимосвязь между ними

Поступательное s	Вращательное	Взаимосвязь
,
,	,	,
		,
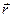