Задачи для самостоятельного решения. 2.2.1.Разделите многочлен р(z) на многочлен q(z):
2.2.1.Разделите многочлен р(z) на многочлен q(z):
а) р(z) = 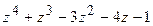 , q(z)=
, q(z)= 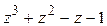 ;
;
б) р(х) = 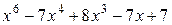 , q(x)=
, q(x)= 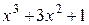 .
.
2.2.2.Найдите все корни многочлена z5 – 2z4 – 6z3 – 6z2 – 7z – 4.
2.2.3.Разложите на неприводимые множители на множестве действительных чисел многочлены:
а) 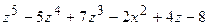 ,
,
б) 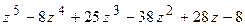 .
.
Тест для самоконтроля
по теме «Многочлены»
1. Для многочлена 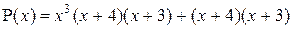 сумма всех действительных корней равна …
сумма всех действительных корней равна …
а) –7; б) –8; в) –6; г) 7.
2. Дан многочлен 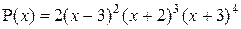 . Установите соответствие между корнями многочлена (список 1–4) и их кратностью (список а – д).
. Установите соответствие между корнями многочлена (список 1–4) и их кратностью (список а – д).
1) 2; 2) – 2; 3) 3; 4) –3;
а) 1; б) не является корнем; в) 2; г) 3; д) 4.
3. Действительными корнями многочлена 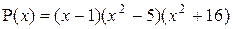 являются:
являются:
а) 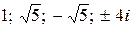 ; б)
; б) 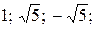 в)
в) 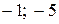 ; г)
; г) 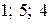 .
.
4. Число действительных корней многочлена 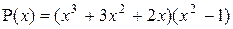 с учетом их кратности равно
с учетом их кратности равно
а) 3; б) 1; в) 2; г) 5.
5. Два многочлена равны между собой тогда и только тогда, когда равны их:
а) корни; б) коэффициенты;
в) переменные; г) степени.
6. Среди многочленов равными являются (укажите набор):
а) 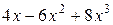 ; б)
; б) 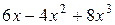 ; в)
; в) 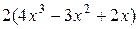 ; г)
; г) 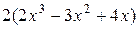 ; д)
; д) 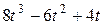 ; е)
; е) 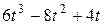 .
.
7. При умножении многочленов 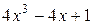 и
и 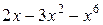 получается многочлен степени:
получается многочлен степени:
а) 4; б) 6; в) 9; г) 18.
8. При умножении многочленов 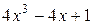 и
и 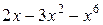 получается многочлен, старший коэффициент которого равен:
получается многочлен, старший коэффициент которого равен:
а) 8; б) 4; в) -12; г) -4.
9. Установите соответствие между операцией над многочленами (список 1–3) и ее результатом (список а–е):
1) 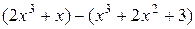 ;
;
2) 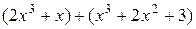 ;
;
3) 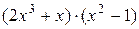 ;
;
а) 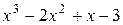 ; б)
; б) 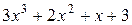 ; в)
; в) 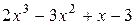 ;
;
г) 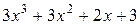 ; д)
; д) 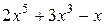 ; е)
; е) 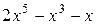 .
.
10. При делении многочлена 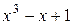 на двучлен
на двучлен 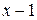 в остатке получится
в остатке получится
а) 0; б) 1; в) 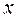 ; г)
; г) 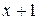 .
.
11. Частное от деления многочлена 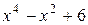 на многочлен
на многочлен 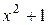 равно:
равно:
а) 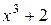 ; б)
; б) 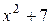 ; в)
; в) 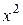 ; г)
; г) 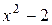 .
.
12. Остаток от деления многочлена 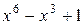 на многочлен
на многочлен 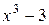 равен:
равен:
а) 0; б) 7; в) 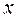 ; г)
; г) 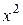 .
.
13. Пусть 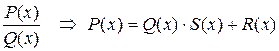 . Установите соответствие между многочленами (список 1–4) и их названиями (а–е) то многочлен называется … от деления многочлена на многочлен.
. Установите соответствие между многочленами (список 1–4) и их названиями (а–е) то многочлен называется … от деления многочлена на многочлен.
1. 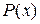 ; 2)
; 2) 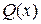 ; 3)
; 3) 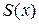 ; 4)
; 4) 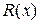 ;
;
а) частное; б) делитель; в) числитель;
г) остаток; д) делимое; е) знаменатель.
14. Число а является корнем многочлена 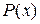 тогда и только тогда, когда (выберите верные ответы):
тогда и только тогда, когда (выберите верные ответы):
а) выполняется условие 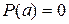 ;
;
б) 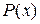 делится без остатка на
делится без остатка на 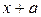 ;
;
в) выполняется условие 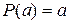 ;
;
г) 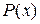 делится без остатка на
делится без остатка на 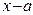 ;
;
д) 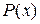 делится без остатка на а.
делится без остатка на а.
15. Число а является k-кратным корнем многочлена 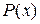 тогда и только тогда, когда:
тогда и только тогда, когда:
а) 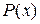 делится на
делится на 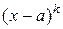 , но не делится на
, но не делится на 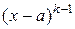 ;
;
б) 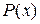 делится на
делится на 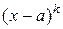 , но не делится на
, но не делится на 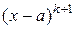 ;
;
в) 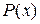 делится на
делится на 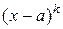 , но не делится на
, но не делится на 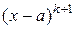 и
и 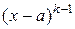 ;
;
г) 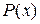 делится на
делится на 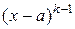 , но не делится на
, но не делится на 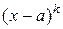 .
.
16. Корень многочлена называется простым, если его кратность равна:
а) 0; б) 1; в) 2; г) –1.
17. Если многочлен 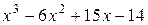 имеет целые корни, то их нужно искать среди делителей числа:
имеет целые корни, то их нужно искать среди делителей числа:
а) –6; б) 15; в) –14; г) 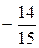 .
.
Не оставляйте без внимания и приведенные ниже контрольные вопросы. Работа над ними покажет уровень усвоения вами темы «Многочлены» и послужит подготовкой к защите раздела «Комплексные числа и многочлены».
2.3. Контрольные вопросы
1. Может ли квадратное уравнение с действительными коэффициентами иметь корни 1 + i и 1-2i ? Ответ обоснуйте.
2. Многочлен z4 + 4z3 + 11z2 + 14z + 10 разложить на множители первой и второй степени с действительными коэффициентами, если известен один корень z1 = –1 + i.
3. При каких значения А и В многочлен 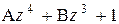 делится на многочлен (z – 1)2 без остатка?
делится на многочлен (z – 1)2 без остатка?
4. При каком значении а число z = 2i является корнем многочлена
z3 – (a + 1)z2 + 4аz + 8(а2 – 2)?
5. Определите a так, чтобы один из корней уравнения z3 –7z + a = 0 равнялся удвоенному другому.
6. Определите a, b, c так, чтобы они были корнями уравнения
z3– az2 + bz+ c = 0.
7. Докажите, что всякий многочлен третьей степени приводим на множестве действительных чисел.
8. Докажите, что число 1 является корнем многочлена тогда и только тогда, когда сумма его коэффициентов равна 0.
9. При каком значении а Î R число 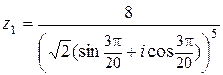 является корнем многочлена z3 – (a+3)z2 + 6a2z + a2 – 5. Найдите остальные корни этого многочлена при найденном значении а.
является корнем многочлена z3 – (a+3)z2 + 6a2z + a2 – 5. Найдите остальные корни этого многочлена при найденном значении а.
13. Решите уравнение z8 +6z4 +9 = 0.
15. Производной (первого порядка) многочлена 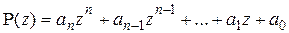 по переменной z называется многочлен вида
по переменной z называется многочлен вида 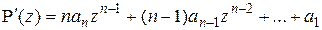 ¢(z). Производная от многочлена
¢(z). Производная от многочлена 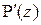 называется производной второго порядка от многочлена
называется производной второго порядка от многочлена 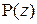 , и т.д., производная
, и т.д., производная 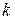 -го порядка от многочлена
-го порядка от многочлена 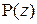 определяется по правилу
определяется по правилу 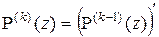 . Производная от многочлена нулевой степени и от нуля считается равной нулю. Докажите следующие утверждения:
. Производная от многочлена нулевой степени и от нуля считается равной нулю. Докажите следующие утверждения:
а) Р(п)(z) = п!ап;
б) Если число a является т-кратным корнем многочлена Р(z), то это число является (т – 1)-кратным корнем первой производной этого многочлена;
в) Если число a является т-кратным корнем многочлена Р(z), то это число является (т – k)-кратным корнем k-й производной этого
многочлена (m ³ k), но не будет корнем его т-й производной.
Рациональные дроби.
