Функции для преобразования полиномов

а) Expand[poly] - раскрыть произведения и степени в выражении poly.

In[1]:= t = (2 + 4 x^2)^2 (x - 1)^3;

In[2]:= Expand[t]

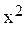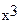Out[2]= 4 + 12x - 28 + 52 - 64 + - +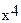

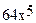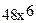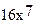
b) Factor[poly] - представить выражение в виде множителей. Коэффициенты полинома должны быть целыми или рациональными числами.

In[3]:=Factor [%] , где % - результат предыдущих вычислений (Out[2])

Out[3] = 4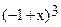

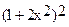
c) Collect[poly] - выносит целый множитель или представляет выражение как полином от некоторой переменной.

Collect[poly, x] - представляет выражение, как полином от x.

In[4]:=u = (1 + 2 x + y)^3;

In[5]:= Collect[u,x]

Out[5]=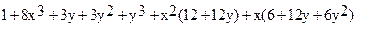

d) Simplify[expr] - упрощает выражение expr.

In[6]:= Simplify[%]

Out[6]=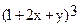

Функции определения структуры полинома

а) PolynomialQ[expr, x] - возвращает True, если expr полином от x.

b) Variables[poly] - возвращает список переменных полинома.

In[7]:= Variables[u]

Out[7]= {x, y}

c) Length[poly] - возвращает число терминов, входящих в полином.

In[8]:= Length[u]

Out[8]= 2

d) Exponent[poly, x] - возвращает максимальную степень в полиноме при y.

In[9]:=Exponent[u, y]

Out[9]= 3

Функции преобразования рациональных выражений

a) Numerator[expr] - возвращает числитель выражения expr.

b) Denumenator[expr] - возвращает знаменатель выражения expr.

c) Expand[expr] - раскрывает степени и произведения полиномов в числителе, оставляя знаменатель в виде простейших множителей.

In[1]:= V=(x - 1)^2 (2 + x) / ((1 + x) (x - 3)^2);

In[2]:= Expand[V]

Out[2]= - +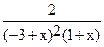

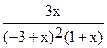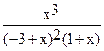
d) ExpandAll[expr] - тоже что и Expand для числителя, в знаменателе раскрываются произведения и степени.

In[3]:=ExpandAll[V]

Out[3]= - +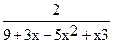

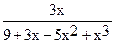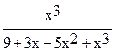
e) Together[expr] - приведение к общему знаменателю.

In[4]:= Together[%]

Out[4]=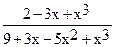

f) Apart[expr] - возвращает выражение в виде суммы с простыми знаменателями.

In[5]:= Apart [%]

Out[5]=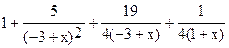

g) Factor[expr] - представляет рациональное выражение в виде множителей.

In[6]:=Factor[%]

Out[6]=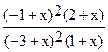

h) Simplify[expr] - упрощает выражение, представляя его в компактной форме

In[7]:= Simplify[%%]

Out[7]=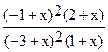

Символьная математика

Базовые функции

a) Дифференцирование функций :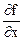

D[f,u] - частная производная функции f по u;

In[1]:= D[Sin[x^2]*x, x]

Out[1]:= 2 x² Cos[ x² ] + Sin[ x² ]

In[2]:= D[ x^2 * y^2 , y, x]

Out[2]:= 4 x y

D[f,{x, n}] - частная производная функции f по x n-го порядка.

In[3]:= D[Sin[ x ]*x^2, {x, 2}]

Out[4]:= 4 x Cos[ x ] + 2 Sin[ x ] - x² Sin[ x² ]

b) Интегрирование выражений:

Integrate[f,x] - неопределенный интеграл ;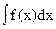

In[1]:= Integrate[ x * Sin[ x ], x]

Out[1]:= -x Cos[ x ] + Sin[ x ]

Integrate 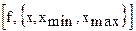- определенный интеграл ;

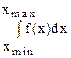In[1]:= Integrate[ x * Sin[ x ], {x, -10, 10)]

Out[1]:= -20 Cos[ 10 ] + 2 Sin[ 10 ]

Integrate - .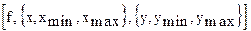

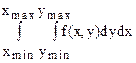In[1]:= Integrate[ x^2 + y^2, {x, 0, 1}, {y, 0, 1}]

Out[1]:= 1/3

c) Сумма, разложение в ряд и нахождение пределов:

Sum 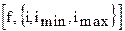- сумма по i;

In[1]:= Sum[ x^n/(n!), {n, 1, 5}]

Out[1]:= x + x^2/2 + x^3/6 + x^4/24 + x^5/120

Series 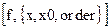- разложение в степенной ряд ;

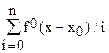In[1]:= Series[ f[x], {x, 0, 3}]

Out[1]:=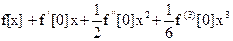

Limit 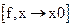- предел .

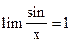Уравнения

Правила записи уравнений.

Уравнения в системе Mathematica записываются как тождества. Для их запис используется знак двойного равенства < == >.

a) Одно уравнение:

lhs == rhs , где rhs - правая часть уравнений, lhs - левая часть уравнения.

a) Система уравнений:

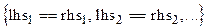, где уравнения представляются в виде списка

ПРИМЕР записи уравнений:

a x^2+b x+c == 0 запись одного уравнения

{ a x^2+b x+c == 0, a x+b == 0} запись системы 2-х уравнений