Тема 4. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами.
Основною задачею в диференціальних рівняннях є знаходження їхнього загального розв’язку. Ця задача найповніше вивчена для лінійних рівнянь із сталими коефіцієнтами.
Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами.
Розглянемо лінійне однорідне рівняння другого порядку
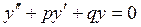 ( 1 )
( 1 )
де 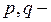 дійсні числа.
дійсні числа.
Ейлер запропонував шукати частинні розв’язки цього рівняння у вигляді 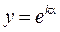 , де
, де 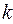 – стала (дійсна чи комплексна), яку треба знайти. Підставивши функцію
– стала (дійсна чи комплексна), яку треба знайти. Підставивши функцію 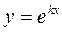 в рівняння 1, дістанемо
в рівняння 1, дістанемо
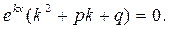
Оскільки 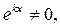 то
то
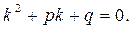 ( 2 )
( 2 )
Отже, якщо 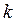 буде коренем рівняння 2, то функція
буде коренем рівняння 2, то функція 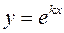 буде розв’язком рівняння 1. Квадратне рівняння 2 називається характеристичним рівнянням диференціального рівняння 1.
буде розв’язком рівняння 1. Квадратне рівняння 2 називається характеристичним рівнянням диференціального рівняння 1.
Позначимо корені характеристичного рівняння через 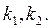 можливі три випадки:
можливі три випадки:
І. 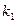 і
і 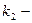 дійсні і різні числа
дійсні і різні числа 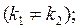
ІІ. 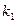 і
і 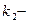 комплексні числа
комплексні числа 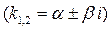 ;
;
ІІІ. 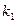 і
і 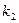 - дійсні і рівні числа
- дійсні і рівні числа 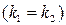 .
.
Розглянемо кожен випадок окремо.
І.Корені характеристичного рівняння дійсні і різні: 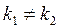 . У цьому випадку частинними розв’язками рівняння 1 є функції
. У цьому випадку частинними розв’язками рівняння 1 є функції 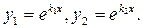
Ці розв’язки лінійно незалежні, тому що при 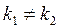
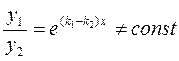 .
.
Загальний розв’язок рівняння 1 знаходять за формулою 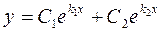 . ( 3 )
. ( 3 )
ІІ.Корені характеристичного рівняння комплексно – спряжені:
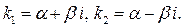
Підставивши значення 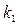 та
та 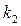 у формулу
у формулу 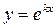 ,знайдемо розв’язки
,знайдемо розв’язки
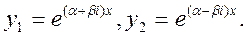
За формулою Ейлера
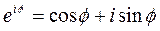
маємо
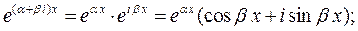
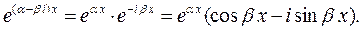
Зауважимо ,що коли функція 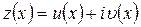 є розв’язком рівняння 1, то розв’язками будуть також функції
є розв’язком рівняння 1, то розв’язками будуть також функції 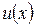 та
та 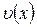 . Дійсно, підставивши функції
. Дійсно, підставивши функції 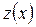 в рівняння 1, дістанемо:
в рівняння 1, дістанемо:
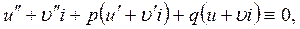
або
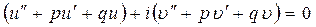
Остання тотожність можлива, коли вирази в дужках дорівнюють нулю. Це означає , що функції 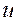 та
та 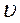 - розв’язки рівняння 1. Згідно з цим зауваженням частинними розв’язками рівняння 1 є функції
- розв’язки рівняння 1. Згідно з цим зауваженням частинними розв’язками рівняння 1 є функції 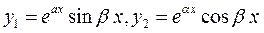 .
.
Ці розв’язки лінійно незалежні, оскільки
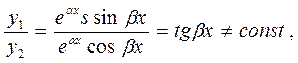
тому загальний розв’язок рівняння 1 запишеться у вигляді
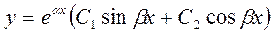 ( 4 )
( 4 )
ІІІ.Корені характеристичного рівняння дійсні і рівні: 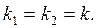 За формулою
За формулою 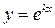 дістанемо один з розв’язків :
дістанемо один з розв’язків : 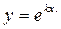 .
.
Другий розв’язок шукатимемо у вигляді 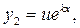 де
де 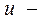 невідома функція від
невідома функція від 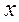 . Знайшовши
. Знайшовши 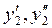 та підставивши їх у рівняння 1 дістанемо:
та підставивши їх у рівняння 1 дістанемо:

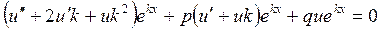
або
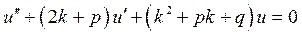
Оскільки 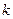 - корінь рівняння 2, то
- корінь рівняння 2, то 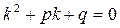 і за теоремою Вієта
і за теоремою Вієта 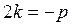 , тому
, тому 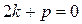 і
і 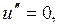 звідки
звідки 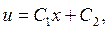 де
де 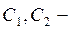 довільні сталі. Поклавши
довільні сталі. Поклавши 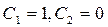 (нас цікавить розв’язок
(нас цікавить розв’язок 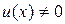 ), знайдемо другий частинний розв’язок рівняння 1:
), знайдемо другий частинний розв’язок рівняння 1:
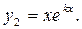
Розв’язки 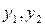 - лінійно незалежні, тому загальний розв’язок рівняння 1 має вигляд:
- лінійно незалежні, тому загальний розв’язок рівняння 1 має вигляд:
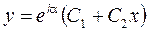 . ( 5 )
. ( 5 )
Приклад 1.
Розв’язати рівняння: 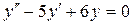 .
.
Розв’язання :
Складемо характеристичне рівняння 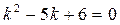 і знайдемо його корені
і знайдемо його корені 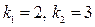 за формулою
за формулою 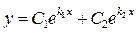 шуканий розв’язок має вигляд:
шуканий розв’язок має вигляд:
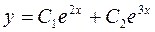 .
.
Приклад 2.
Розв’язати рівняння: 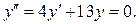
Розв’язання:
Характеристичне рівняння 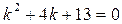 має комплексні корені
має комплексні корені 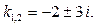 Загальний розв’язок дістанемо за формулою ( 4 ):
Загальний розв’язок дістанемо за формулою ( 4 ):
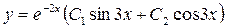 .
.
Приклад 3.
Розв’язати рівняння: y²+2y¢+y=0.
Розв’язання:
Будуємо характеристичне рівняння 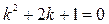 , звідки
, звідки 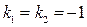 .
.
Отже, загальний розв’язок: 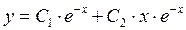 .
.
