Двусторонняя проверка проверяет значимость, когда взаимосвязь между Х иY может быть и положительной, и отрицательной.
Для проверки статистической надежности можно использовать интервальное оценивание коэффициентов регрессии.
Для значений параметров модели bj, j = 0,1,2,…,p строятся доверительные интервалы, которые будут приемлемы с вероятностью (1 – a) при найденных оценках bj:
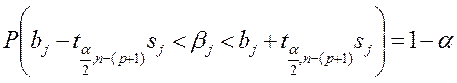 ,
,
где 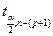 – табличное значение статистики Стьюдента при выбранном
– табличное значение статистики Стьюдента при выбранном
уровне значимости и n – (p + 1) степенях свободы;
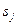 –стандартная ошибка оценки, равная:
–стандартная ошибка оценки, равная: 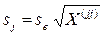 .
.
Вывод о статистической надежности оценки делают исходя из знаков границ доверительного интервала: если эти знаки одинаковы, то нулевая гипотеза о равенстве истинного значения параметра нулю отклоняется в пользу альтернативной гипотезы при вероятности (1 –a); в противном случае нулевая гипотеза не отклоняется, и соответствующий коэффициент bj считается статистически не значимой характеристикой параметра.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 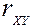 . Существуют различные формулы для его определения:
. Существуют различные формулы для его определения:
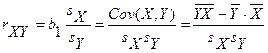 .
.
Как известно, линейный коэффициент корреляции находится в границах:
-1 £ 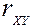 £ 1.
£ 1.
Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между переменными может оказаться достаточно тесной.
Проверка общего качества уравнения регрессии.
Коэффициент детерминации
Для оценки качества подбора линейной функции (близости расположения фактических данных к рассчитанной линии регрессии)рассчитывается квадрат линейного коэффициента корреляции 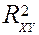 , называемый коэффициентом детерминации.
, называемый коэффициентом детерминации.
Проверка осуществляется на основе исследования коэффициента детерминации и проведения дисперсионного анализа.
Регрессионная модель показывает, что вариация Y может быть объяснена вариацией независимой переменной Х и значением возмущения e. Мы хотим знать, насколько вариация Y обусловлена изменением Х и насколько она является следствием случайных причин. Другими словами, нам нужно знать, насколько хорошо рассчитанное уравнение регрессии соответствует фактическим данным, т.е. насколько мала вариация данных вокруг линии регрессии.
Для оценки степени соответствия линии регрессии нужно рассчитать коэффициент детерминации, суть которого можно хорошо уяснить, рассматривая разложение общей суммы квадратов отклонений переменной Y от среднего значения 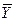 на две части – «объясненную» и «необъясненную» (рис. 4).
на две части – «объясненную» и «необъясненную» (рис. 4).
Из рис. 4 видно, что 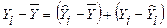 .
.
Возведем обе части этого равенства в квадрат и просуммируем по всем i от 1 до n.
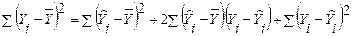
Перепишем сумму произведений в виде:
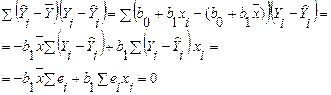
Здесь использованы следующие свойства:
1)  ;
;
2) метод наименьших квадратов (МНК)исходит из условия:
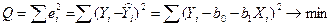 .
.
необходимым условием существования минимума функции Q является равенство нулю ее первых частных производных по b0 и b1.
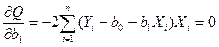 .
.
Или 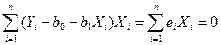 .
.
Отсюда следует, что 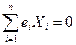 .
.
 |
 Y
Y
 |

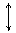



 Yi
Yi

 е1
е1




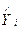





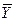
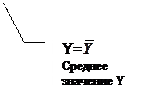 | |||||
 | |||||
 | |||||
 0
0
Хi Х
Рисунок 4. Структура вариации зависимой переменной Y
Таким образом, в результате будем иметь:
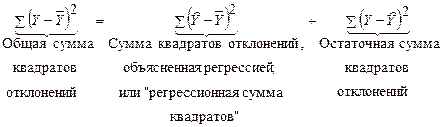 (1)
(1)
Общая сумма квадратов отклонений индивидуальных значений зависимой переменной Y от среднего значения 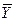 вызвана влиянием множества причин, которые мы условно разделили на две группы: фактор Х и прочие факторы (случайные воздействия). Если фактор Х не оказывает влияния на результат (Y), то линия регрессии на графике параллельна оси абсцисс и
вызвана влиянием множества причин, которые мы условно разделили на две группы: фактор Х и прочие факторы (случайные воздействия). Если фактор Х не оказывает влияния на результат (Y), то линия регрессии на графике параллельна оси абсцисс и 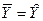 . Тогда вся дисперсия зависимой переменной Y обусловлена воздействием прочих факторов, и общая сумма квадратов отклонений совпадает с остаточной суммой квадратов. Если же прочие факторы не влияют на результат, то Y связан с Х функционально, и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
. Тогда вся дисперсия зависимой переменной Y обусловлена воздействием прочих факторов, и общая сумма квадратов отклонений совпадает с остаточной суммой квадратов. Если же прочие факторы не влияют на результат, то Y связан с Х функционально, и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
Разделим обе части уравнения (1) на левую часть (на общую сумму квадратов), получим:
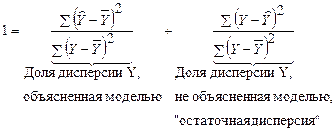 (2)
(2)
Доля дисперсии зависимой переменной, объясненная регрессией, называется коэффициентом детерминации и обозначается R2. Из (2) коэффициент детерминации определяется:
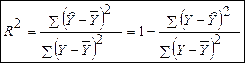 . (3)
. (3)
Величина коэффициента детерминации находится в пределах от 0 до 1 и служит одним из критериев проверки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно пользоваться для прогноза значений результативного признака.
коэффициент детерминации принимает значения от нуля, когда х не влияют на У, до единицы, когда изменение У полностью объясняется изменением х. Таким образом, коэффициент детерминации характеризует «полноту» модели.
Преимущества коэффициента детерминации: он легко вычисляется, интуитивно понятен и имеет четкую интерпретацию. Но несмотря на это его использование иногда связано с проблемами:
· нельзя сравнивать величины R2 для моделей с различными зависимыми переменными;
· R2 всегда возрастает по мере включения новых переменных в модель. Это свойство R2 может создавать у исследователя стимул необоснованно включать дополнительные переменные в модель, и в любом случае становится проблематичным определить, улучшает ли дополнительная переменная качество модели;
· R2 малопригоден для оценки качества моделей временных рядов, т.к. в таких моделях его значение часто достигает величины 0,9 и выше; дифференциация моделей на основании данного коэффициента является трудновыполнимой задачей.
Одна из перечисленных проблем – увеличение R2 при введении в модель дополнительных переменных – решается путем коррекции коэффициента на уменьшение числа степеней свободы в результате появления в модели дополнительных переменных.
Скорректированный коэффициент детерминации рассчитывается так:
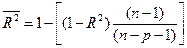 , (4)
, (4)
Как видно из формулы, при добавлении переменных 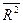 будет увеличиваться только в том случае, если рост R2 будет «перевешивать» увеличение количества переменных. Действительно,
будет увеличиваться только в том случае, если рост R2 будет «перевешивать» увеличение количества переменных. Действительно,
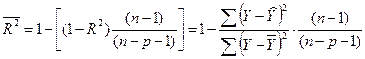 ,
,
т.е. доля остаточной дисперсии с включением новых переменных должна уменьшаться, но, умноженная на 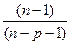 она, в то же время, будет расти с ростом числа включенных в модель переменных (р); в итоге, если положительный эффект от включения новых факторов «перевесит» изменение числа степеней свободы, то
она, в то же время, будет расти с ростом числа включенных в модель переменных (р); в итоге, если положительный эффект от включения новых факторов «перевесит» изменение числа степеней свободы, то 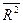 увеличится; в противном случае – может и уменьшиться.
увеличится; в противном случае – может и уменьшиться.
Оценка качества уравнения (адекватности выбранной модели эмпирическим данным) производится с помощью F-теста. Суть оценки сводится к проверке нулевой гипотезы Н0 о статистической незначимости уравнения регрессии и коэффициента детерминации. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера:
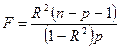 . (5)
. (5)
В случае справедливости гипотезы
Н0: b0 = b1 = … = bр = 0 (или R2истин = 0)
статистика Fфакт должна подчиняться F – распределению с числом степеней свободы числителя и знаменателя, соответственно равными
n1 = р и n2 = n – p – 1.
Табличное значение F-критерия для вероятности 0,95 (или 0,99) и числа степеней свободы n1 = р, n2= n – p – 1 сравнивается с вычисленным; при выполнении неравенства F > Fтабл отвергается нулевая гипотеза о том, что истинное значение коэффициента детерминации равно нулю; это дает основание считать, что модель адекватна исследуемому процессу.
Для парной модели в критерии проверки для R2 числителю соответствует одна степень свободы и (n – 2) степеней свободы соответствует знаменателю. Расчет F-критерия для проверки значимости R2 выполняется следующим образом:
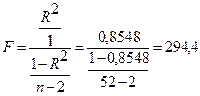 .
.
Обратившись к F-таблице, видим, что табличное значение при 5%-м уровне значимости для n1 = 1 и n2 = 50 составляет примерно 4. Так как расчетное значение F-критерия больше табличного, то при доверительной вероятности 0,95 отвергаем нулевую гипотезу о том, что истинное значение коэффициента детерминации равно нулю.
Таким образом, можно сделать вывод о том, что коэффициент детерминации (а значит, и модель в целом) являются статистически надежным показателем взаимосвязи рассматриваемых фондовых индексов.
Квадратный корень из величины коэффициента детерминации для парной модели является коэффициентом корреляции– показателем тесноты связи.
Третья стадия – проверка выполнимости основных предпосылок классической регрессии – предмет дальнейшего изучения.
