Метод рационализации неравенств

Отметим, что нестандартность этого метода заключается в том, что его изучение не входит в школьную программу, и он отсутствует в учебниках для общеобразовательной школы. Часть подобных неравенств могла быть решена сведением к совокупности двух систем.

При решении логарифмических неравенств метод рационализации опирается на следующее утверждение.

Утверждение 1.Знак выражения 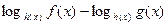совпадает со знаком выражения 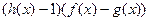, где , .

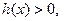
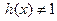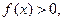
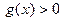В частности, знак выражения 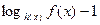совпадает со знаком выражения 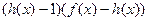, а знак выражения 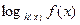совпадает со знаком выражения .

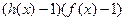Доказательствопроведем в два этапа.

1. Пусть 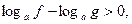т.е. 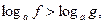причем

. ( )

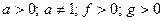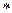Если число 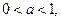то по свойству убывающей логарифмической функции имеем 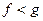. Значит, выполняется система неравенств

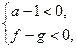
откуда следует неравенство 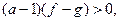верное на области определения выражения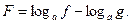

Если числ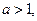о то 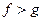. Следовательно, имеет место неравенство

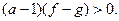
Обратно, если выполняется неравенство 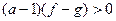на области ( 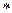), то оно на этой области равносильно совокупности двух систем неравенств

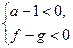и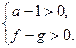

Из каждой системы следует неравенство

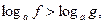т.е.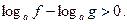

Аналогично, рассматриваются неравенства вида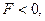

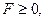
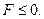
2.Пусть некоторое число 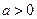и 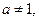тогда имеем

.

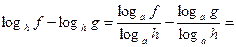
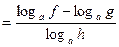Знак последнего выражения совпадает со знаком выражения

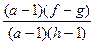или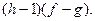

Пример 19. (ЕГЭ 2011). Решить неравенство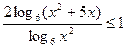

Решение. 1-й способ. Область определения неравенства задается системой

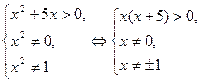
Отсюда получаем, что данное неравенство определено при всех значениях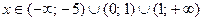

.

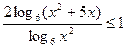
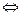
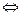
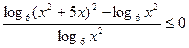Используем рационализацию последнего неравенства

.

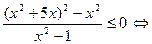
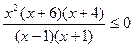Отсюда решения 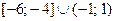. Учитывая ОДЗ, находим окончательно .

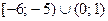Решение. 2-й способ. Множество 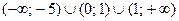– область определения данного неравенства.

Приведем данное неравенство к виду

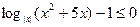
или

.

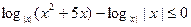Так как знак выражения совпадает со знаком выражения 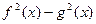([1], стр. 22), то получим

.

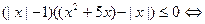
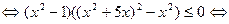
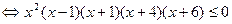Последнее неравенство имеет решения 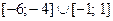. С учетом ОДЗ получим .

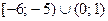Ответ: .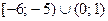

Пример 20.Решить неравенство

.

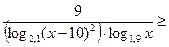
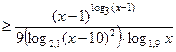Решение. Область определения неравенства задается системой

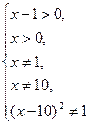или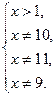

Учитывая, что при 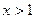выражение 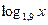положительно, преобразуем данное неравенство на его области определения

.

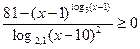Для решения последнего неравенства используем метод рационализации:

.

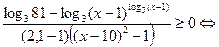
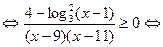
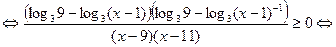
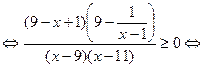
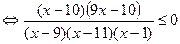Ответ. .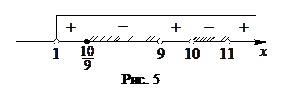

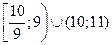Используем метод рационализации еще к одному виду логарифмических неравенств ([1], стр. 22).

Утверждение 2.Знак выражения 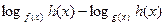совпадает со знаком выражения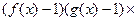 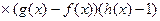, где , .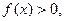

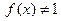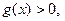
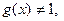
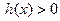Доказательство. Так как

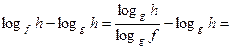
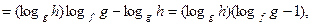
то, используя рационализацию неравенств, получаем, что знак последнего выражения совпадает со знаком выражения

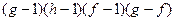или

.

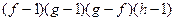Решим выше рассмотренный пример 6.

Пример 21.Решить неравенство

.

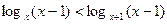Решение.Данноенеравенство приведем к следующему виду

,

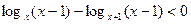которое равносильно системе неравенств

.

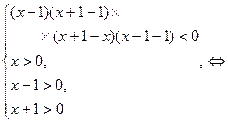
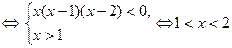Ответ: .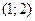

Метод оценки

Иногда неравенство 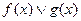устроено так, что на всей ОДЗ неизвестной имеют место неравенства 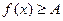и 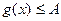при некотором А. В этом случае:

а) решение неравенства 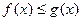сводится к нахождению тех значений 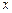, для которых одновременно 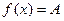и ;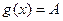

б) решение неравенства 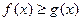сводится к нахождению тех решений неравенства 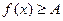, для которых определена функция .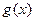