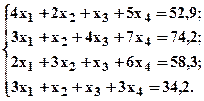Решение систем линейных алгебраических уравнений
Краткие теоретические сведения:
Для того, чтобы системы линейных алгебраических уравнений имела единственное решение необходимо и достаточно, чтобы определитель системы, составленный из коэффициентов при переменных не был равен нулю.
Для решения системы линейных алгебраических уравнений следует выполнить следующую последовательность действий:
· Записать уравнения в матричной форме (матрица коэффициентов, умноженная на вектор неизвестных, равняется известному вектору правой части уравнения).
· Рассчитать определитель матрицы коэффициентов. Если его значение не равно нулю, можно продолжить процесс поиска решений.
· Обратить матрицу коэффициентов.
· Умножить правую и левую части уравнения на матрицу, обратную матрице коэффициентов.
В результате выполнения четвертого шага получим вектор, компонентами которого будут искомые неизвестные.
Пример выполнения:
Задание. Решить систему уравнений:
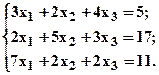
Решение:
1. Запись системы уравнений в матричной форме.
Запишем неизвестные х1, х2 и х3 в виде вектора неизвестных [x]:
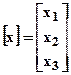 .
.
Коэффициенты системы соберем в матрицу коэффициентов [С]:
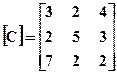
Константы, стоящие в правых частях уравнений, запишем в виде вектора 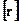 :
:
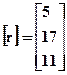
Таким образом, приведенные выше три уравнения для трех неизвестных можно записать как
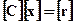 .
.
Таблица Excel, в которую введены матрица [С] и вектор 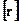 , приведена на рис. 1.
, приведена на рис. 1.
2. Расчет определителя матрицы коэффициентов.
Рассчитаем определитель матрицы коэффициентов, пользуясь функцией
МОПРЕД(матрица). Рассчитанное значение не равно нулю и, следовательно, можно продолжить процесс поиска решения.
3. Обращение матрицы коэффициентов.
С помощью функции массива МОБР(матрица) найдем матрицу [Собр], обратную матрице [С].
4. Умножение правой и левой частей уравнения на матрицу, обратную матрице [С].
В результате умножения матрицы [С] на обратную матрицу получается единичная матрица. Умножив вектор на единичную матрицу, получим тот же вектор.
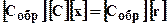 ,
,
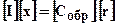 ,
,
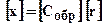 .
.
Таким образом, при умножении матрицы, обратной матрице [С], на вектор 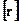 получили решение системы линейных уравнений (рис. 1).
получили решение системы линейных уравнений (рис. 1).
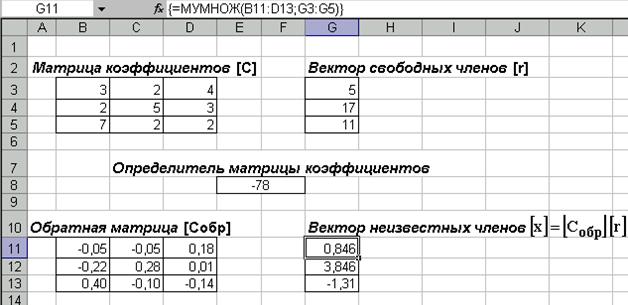
Рис. 1. Таблица Excel с результатами решения системы уравнений
Решением являются такие значения неизвестных:
х1 = 0,846;
х2 = 3,846;
х3 = -1,31.
Задание:
Решите следующие задачи. На рабочих листах Excel создайте таблицы, содержащие исходные данные и результаты вычислений.
- Ниже приведены три системы уравнений, каждая из которых представлена матрицей коэффициентов и вектором правой части. Определите, можно ли решить эти системы уравнений. Решите матричными методами те системы, для которых существует решение.
а) 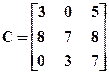
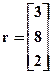 , б)
, б) 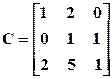
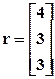 , в)
, в) 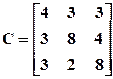
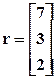
- Запишите приведенные ниже системы уравнений в матричной форме и проверьте, есть ли у них решения. Решите матричными методами те системы, для которых существует решение.
а) 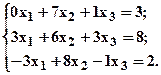 б)
б) 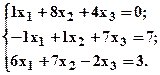
в) 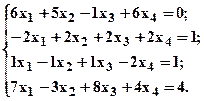
- Запишите приведенные ниже системы уравнений в матричной форме и найдите их решения (если это возможно).
а) 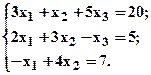 б)
б) 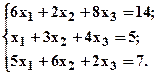 в)
в)