Тема урока. Сложение многозначных чисел без перехода через разряд.

Цели урока:1)распространить алгоритм сложе­ния трехзначных чисел на многозначные числа;

2) преобразовывать единицы площади.

3) развивать навык устных и письменных вычислений;

4) снижать уровень тревожности на уроке;

5 )воспитывать интерес к урокам математики

Ход урока

1.Организационный момент

2. Проверка домашнего задания

3. Устный счёт

4.Работа по учебнику

(У) Задания4, 7, 5*.

Задание 4.В числе 269 354 всего: 269 354 едини­цы, 26 935 десятков, 2693 сотни, 269 тысяч, 26 де­сятков тысяч, 2 сотни тысяч.

Задание 5*. Чтобы решить задачу, нужно урав­нять количество синиц на деревьях. Это можно сде­лать разными способами: убрать с деревьев лишних синиц (4, 6 и 8); добавить на первое дерево 4 синиц, а на другое — двух; перенести двух синиц с третьего дерева на первое. Каждый из этих способов приводит к разным способам решения задачи.

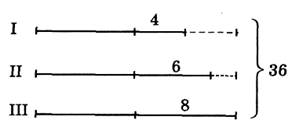
Способ I.

1) 36 - (4 + 6 + 8) = 18 (с.) — стало бы всего синиц;

2) 18 : 3 = 6 (с.) — было бы на каждом дереве;

3) 6 + 4 = 10 (с.) — сидело на первой березе;

4) 6 + 6 = 12 (с.) —сидело на второй березе;

5) 6 + 8 = 14 (с.) — сидело на третьей березе.

Задание 7. Р = 3 дм 5 см + 3 дм 5 см + 2 дм = 3 дм 5 см • 2 + 2 дм = 9 дм.

5.Работа в тетрадях

(П) Задания 1, 2, 3, 8, 9, 6.

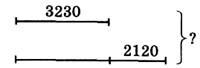Задание 2.

Было — ?

Взяли — 3230 кг.

Осталось — ?, на 2120 кг больше.

(3230 + 2120) + 3230 = 8580 (кг). (Вычисления мож­но выполнять в столбик.)

Задание 3. 1)12:2 = 6 (см) — длина;

2) (6 + 2) • 2 = 16 (см) — периметр.

Задание 6. По частям нужно найти два числа и сравнить их.

12 ∙ 6 = 72 — первое число; 15 ∙ 8 = 120 — второе число; 72 < 120, 120 - 72 = 48.

Физкультминутка

Задание 9. Сначала уравнения упрощаются: вы­полняются действия с числами. Затем решаются по правилам нахождения неизвестных компонентов сло­жения и вычитания. 24 + 16 + х = 57

40 + х = 57

х = 57- 40

х = 17

24 + 16 + 17 = 57

Д)Задания10, 11.

Задание 10.

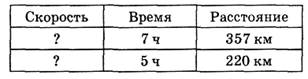Ответ: скорость пассажирского поезда больше скорости товарного на 7км/ч.

7.Подведение итогов урока

8.Рефлексия

Урок 50

Тема урока. Сложение многозначных чисел с пе­реходом через разряд.

Цели урока:1)закрепить алгоритм сложения многозначных чисел с переходом через разряд;

2) отрабатывать навыки преобразования величин.

3) развивать навык устных и письменных вычислений;

4) снижать уровень тревожности на уроке;

5 )воспитывать интерес к урокам математики

Ход урока

1.Организационный момент

2. Проверка домашнего задания

3. Устный счёт

4.Работа по учебнику

(У)Задания1, 7, 8, 5, 6, 4*.

Задание 1.В таблице показан механизм перено­са 10 единиц низшего разряда в виде одной единицы следующего высшего разряда в этот высший разряд. Пользуясь таблицей, ученики должны разъяснить сложение приведенных в качестве примера чисел.

1. Пишем единицы под единицами, десятки под десятками и т. д.

2. Складываем единицы: 7 ед. + 6 ед. = 13 ед.;
13 ед. — это 1 дес. и 3 ед.; 3 ед. пишем под единица­ми, 1 дес. переносим в разряд десятков.

3. Складываем десятки: 4 дес. + 2 дес. = 6 дес; 6 дес. и 1 дес. — 7 дес. Пишем под десятками.

4. Складываем сотни: 8 с.+ 4 с. = 12 с; 12 с.—1 тыс. и 2 с; 2 с. пишем под сотнями, а 1 тыс. пе­реносим в разряд тысяч.

5. Складываем тысячи: 2 тыс. + 1 тыс. = 3 тыс.; 3 тыс. и 1 тыс. — 4 тыс.

Читаем ответ: 4273.

Аналогично объясняется сложение чисел 504 083 и 636 148.

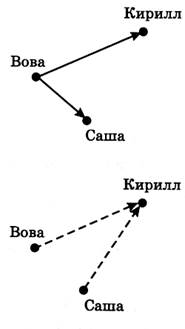Задание 4*. На рисунке сплошные стрелки

обознача­ют «сильнее», а пунктир­ные — «младше».

Из условия видно, что Вова сильнее Кирилла и Саши.

Все стрелки отошли от Вовы, зна­чит, он сильнее всех.

Таким же образом отве­тим на вопрос: «Кто из маль­чиков

самый младший?» Все стрелки на рисунке подошли к Кириллу, значит, он самый младший.

Задание 6. S = а • а. Сторона квадрата — множитель, пло­щадь — произведение. Если каждый множитель увеличить в 2 (или 3) раза, произ­ведение (площадь) увеличится в 4 (или 9) раз. Можно рассмотреть конкретные примеры.

Задание 8. Путем подбора или способом сведения к равенству можно найти значения букв, при которых неравенства будут верными. Например:

х ∙ 6 < 90; х ∙ 6 = 90; х = 90 : 6; х = 15.

Неравенство будет верным при х < 15 и т. д.

Задание 5. Весы уравновешены. Снимем слева и справа сначала по 1 кг, а потом по 200 г. Равновесие сохранится. Слева останется дыня, а справа — 3 кг 800 г. Дыня весит 3 кг 800 г.

5.Работа в тетрадях

Физкультминутка

(П) Задания2, 9, 3.

Задание3. Во сколько раз увеличилось количе­ство овса, во столько же раз увеличится количество ячменя.

120 : 4 = 30 (раз); 3 ∙ 30 = 90 (кг).

Д) Задания 10, 11.

Задание10.

Осталось проехать 264км.

.

7.Подведение итогов урока

8.Рефлексия

Урок 51