Расчет симметричных систем

При расчете симметричных систем можно упростить структуру системы канонических уравнений за счет обращения в ноль как коэффициентов d_ij, так и свободных членов D_ip⁰.

В первом случае соответствующий прием носит название группировки неизвестных, во втором – результат достигается с помощью разложения нагрузки на симметричную и обратносимметричную.

Группировка неизвестных применяется для рам, у которых реакции лишних связей представлены только симметричными неизвестными. Примером служит рама на рис. 4.10, а для выбранной на рис. 4.10, б основной системы, где в канонических уравнениях

d₁₁ X₁ + d₁₂ X₂ + D_1p⁰ = 0;

d₂₁ X₁ + d₂₂ X₂ + D_2p⁰ = 0

все коэффициенты отличны от нуля.

Чтобы упростить эту систему, перейдем от неизвестных X₁ и X₂ к новым неизвестным X₁¢ и X₂¢ по формулам:

X₁¢ = (X₁ + X₂)/2; (4.12)

X₂¢ = (X₁ - X₂)/2

где обратное преобразование:

X₁ = X₁¢+ X₂¢; (4.13)

X₂ = X₁¢- X₂¢

имеет наглядный смысл. При этом неизвестные X₁¢ и X₂¢ соответствуют новой основной системе (рис. 4.10, в), для которой эпюры`M<sub>1</sub><sup>0</sup>¢ и`M₂⁰¢ ортогональны (рис. 4.10, г, д), а d₁₂¢ = 0, поэтому соответствующая система канонических уравнений распадается на два независимых уравнения:

d₁₁¢ X₁¢+ D_1p⁰¢ = 0;

d₂₂¢ X₂¢ + D_2p⁰¢ = 0.

Определив групповые или обобщенные неизвестные X₁¢и X₂¢, можно с помощью (4.13) вернуться к старым переменным X₁ и X₂.

Разложение нагрузки на симметричную и обратносимметричную рассмотрим на следующем примере (рис. 4.11, а), где в соответствии с принципом суперпозиции в такой форме представлена заданная нагрузка (рис. 4.11, б, в). Для выбранной основной системы (рис. 4.11, г) d₁₂ = 0 и расчет от симметричной нагрузки приводит к системе канонических уравнений:

d₁₁ X₁⁽¹⁾+ D_1p⁰⁽¹⁾ = 0; (4.14)

d₂₂ X₂⁽¹⁾ = 0.

При этом D_2p⁰⁽¹⁾ = (`M<sub>2</sub><sup>0</sup> ´ M<sub>p</sub><sup>0(1)</sup>) = 0 в силу ортогональности обратносимметричной эпюры `M₂⁰ и симметричной эпюры M_p⁰⁽¹⁾ от первого загружения (рис. 4.11, б). Поэтому решением (4.14) будет X₁⁽¹⁾ ¹ 0, X₂⁽¹⁾ = 0.

Расчет рамы от второго варианта загружения (рис. 4.11, в) приводит к системе канонических уравнений:

d₁₁ X₁⁽²⁾= 0; (4.15)

d₂₂ X₂⁽²⁾ + D_2p⁰⁽²⁾ = 0,

так как в этом случае равен нулю свободный член D_1p⁰⁽²⁾ = (`M₁⁰ ´ M_p⁰⁽²⁾). Ее решением будет X₁⁽²⁾ = 0, X₂⁽²⁾ ¹ 0.

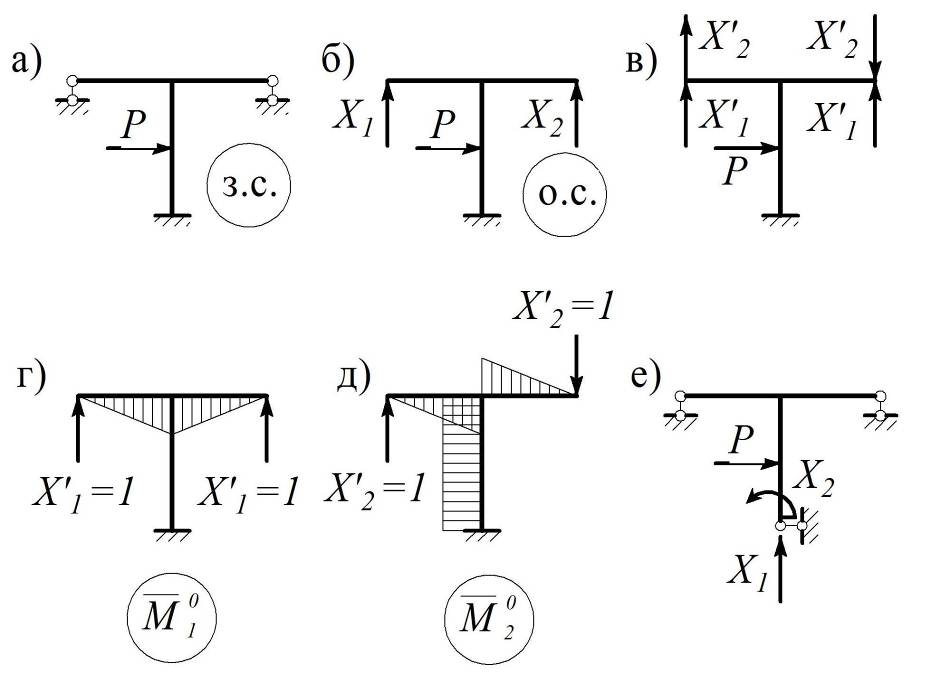
Рис. 4.10

Искомые реакции от заданной первоначальной нагрузки равны сумме соответствующих реакций от каждого варианта загружения:

X₁ = X₁⁽¹⁾ + X₁⁽²⁾ = X₁⁽¹⁾; (4.16)

X₂ = X₂⁽¹⁾ + X₂⁽²⁾ = X₂⁽²⁾.

Основная система

2 загружение

Основная система

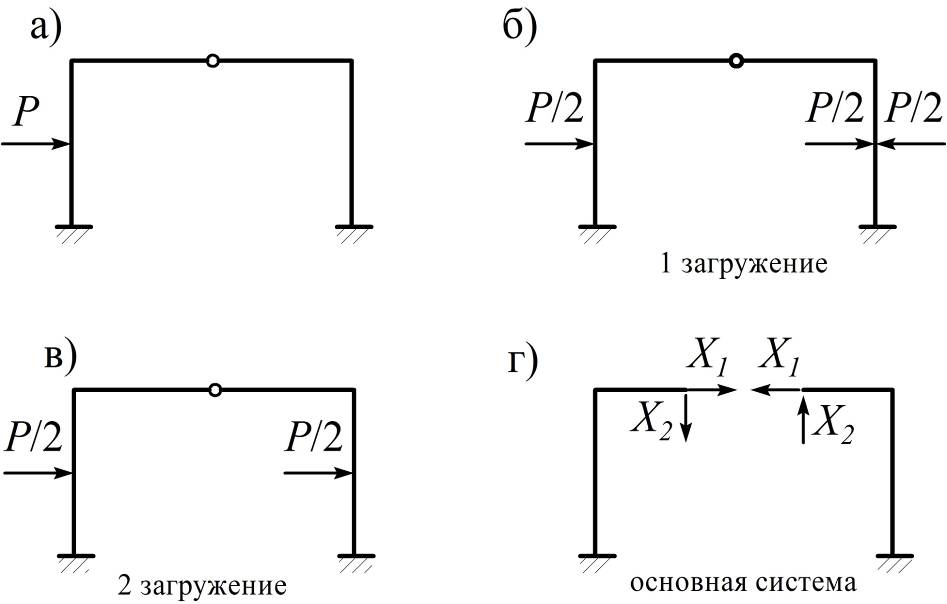
Рис. 4.11

Полученный результат можно сформулировать в виде теоремы.

Теорема. В симметричных системах, загруженных симметричной нагрузкой, обратносимметричные неизвестные равны нулю и наоборот – в симметричных системах, загруженных обратносимметричной нагрузкой, равны нулю симметричные неизвестные.

Примечания

1. Очевидно, что суть рассмотренных методов одинакова: в первом случае суммой симметричных и обратносиметричных сил представляют реакции, во втором – приложенную нагрузку.

2. Рассмотренные приемы расчета удобны для сравнительно простых систем с небольшим числом неизвестных, когда они имеют наглядную интерпретацию. Однако такая идея симметризации неизвестных может быть обобщена на решение произвольных систем алгебраических уравнений.

3. Пример рамы на рис. 4.10, б носит иллюстративный характер – в этом случае решение можно было упростить за счет выбора рациональной основной системы (рис. 4.10, е), для которой d₁₂= (`M<sub>1</sub><sup>0</sup> ´`M₂⁰) = 0.

Расчет неразрезных балок

Неразрезной балкой называется статически неопределимая система, образованная из простой двухопорной балки введением дополнительных промежуточных опор. Эти опоры добавляют в целях уменьшения изгибающих моментов в пролете, и их число равняется степени статической неопределимости полученной системы (рис. 4.12, а).

В отличие от неразрезной балки разрезная или шарнирно-консольная балка является статически определимой системой, она образована из первой введением шарниров во всех пролетах кроме одного и расчет такой составной системы принципиально не отличается от расчета статически определимых рам рассмотренного во второй главе.

Для расчета неразрезных балок можно применить метод сил, выбрав в качестве основной систему, полученную из заданной системы устранением всех промежуточных опор (рис. 4.12, б). Однако такая система не является рациональной, поскольку для нее каждая из эпюр`M_i⁰ и эпюра M_p⁰ отличны от нуля на всей длине балки, а значит, ни один из коэффициентов d_ij и свободных членов D_ip⁰ не равен нулю.

Гораздо эффективнее будет основная система, которая получается из заданной системы введением шарниров над каждой из промежуточных опор (рис. 4.12, в). Она представляет собой цепочку простых двухопорных балок, поэтому каждая из эпюр `M_i⁰ не выходит за пределы двух смежных пролетов (рис. 4.12, г–е). Аналогичное замечание можно сделать и в отношении эпюры M_p⁰, которая также будет иметь локальную структуру (рис. 4.12, ж).

Нетрудно заметить, что независимо от числа промежуточных опор уравнение для i-й опоры неразрезной балки будет иметь вид:

d _{i-1, i} X_i-1 + d_i,i X_i + d _{i+1, i} X _i+1+ D _{i p}⁰ = 0. (4.17)

Это уравнение называется «уравнением трех моментов», поскольку в качестве неизвестных выступают изгибающие моменты над i-й опорой неразрезной балки и еще над двумя опорами, смежными с ней.

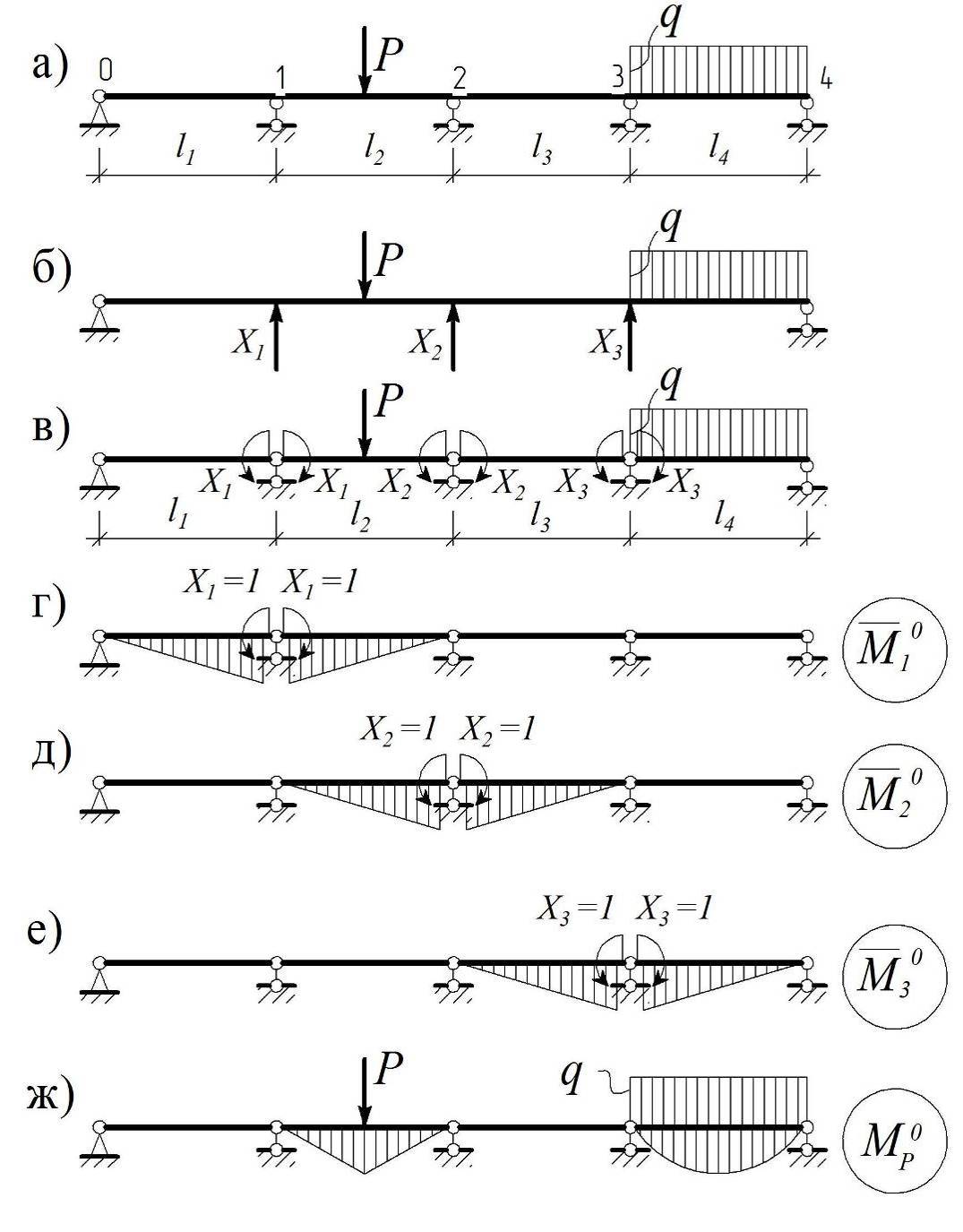
Рис. 4.12

Примечание

В качестве исходной балки для получения неразрезной помимо простой двухопорной балки можно взять балку с одним или двумя жесткозащемленными концами.

Примеры расчета СНС

При расчете СНС реакции связей могут оказаться равными нулю так же, как и при определении опорных реакций СОС.

Пример 4.5. Построить эпюру M_P в раме от заданной нагрузки, полагая EJ = const (рис. 4.13, а).

Решение. Заданная система имеет только одну лишнюю связь, поэтому в качестве основной можно взять систему, полученную из заданной устранением опоры А. Связь в точке С является безусловно необходимой, и ее устранение приводит к мгновенно изменяемой ОС.

X1=1

A

B

C

B

C

B

B

A

A

`M10

MP0

MP

З.С..

A

C

C

а)

б)

в)

г)

Рис. 4.13

Строим эпюры`M₁⁰ и M_p⁰ (рис. 4.13, б-в) для вычисления коэффициента и свободного члена канонического уравнения МС:

d₁₁ X₁ + D_1p⁰ = 0. (а)

Как видим, эти эпюры взаимно ортогональны, d₁₁ ¹ 0, D_1p⁰ = 0, и решением (а) будет X₁ = 0. Поэтому M_p = M_p⁰ +`M₁⁰X₁ = M_p⁰ (рис. 4.13, г). ·

Как уже отмечалось, для системы с одной лишней связью простота решения задачи полностью определяется видом эпюры M_p⁰.

Пример 4.6. Построить эпюру M_P в раме от заданной нагрузки, полагая EJ = const (рис. 4.14, а).

Решение. Отбросив в ЗС опору А, придем к ОС, которой соответствуют эпюры `M₁⁰ и M_p⁰ (рис. 4.14, б-в).

Другой ОС соответствуют эпюры`M<sub>1</sub><sup>0</sup> =`M₁⁰ (рис. 4.14, г) и M_P⁰, при этом последняя заметно проще эпюры M_p⁰ (рис. 4.14, д).

C

е)

ql2/40

A

B

ql2/8

MP0

MP

а)

д)

ql2/2

l

X1=1

A

C

в)

г)

MP0

`M10

q

l

l

A

B

C

X1=1

l

B

C

б)

`M10

З.С.

A

Рис. 4.14

Вычисляя коэффициенты канонического уравнения для EJ = 1, получим:

d₁₁ = (`M<sub>1</sub><sup>0</sup> ´`M₁⁰) = 5l³/3; D_ip⁰ = (`M₁⁰ ´ M_P⁰) = – ql⁴/24,

откуда X₁ = – D_ip⁰/d₁₁ = ql/40.

Правильность найденной эпюры M_p = M_P⁰ +`M₁⁰X₁ (рис. 4.14, е) проверяем с помощью кинематической проверки:

D_1p = (M_p ´`M₁⁰) = – [(2/3)×( l)×(ql²/8)]×(l/4) + [(1/2) ×( l)×(ql²/40)]×(2l/3) +

+ l×(ql²/40)× l +[(1/2)×l×(ql²/40)]×(2l/3) = (ql²/40)[– (1/24) + 2(1/120) + (1/40)] = 0. ·