I. Определение обратной матрицы без определения матриц, обратных треугольным

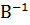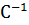Покажем, что обращение матрицы можно произвести и без использования формулы (3.22), т. е. минуя определение матриц и , обратных тем треугольным, на которые разложена матрица А.

Из формулы (3.22) умножением ее обеих частей сначала слева на матрицу В, а потом справа на матрицу С, получаем

.

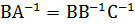Но произведение 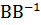матрицы В на обратную ей матрицу 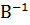есть единичная матрица Е, потому

,

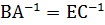(3.23)

а произведение 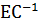единичной матрицы Е на матрицу 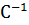оставляет эту последнюю без изменений: 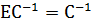. Поэтому (3.23) перепишется так:

.

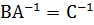(3.24)

Аналогично легко показать, что

.

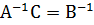(3.25)

Введем такие обозначения:

1) элементы матрицы А будем обозначать через 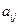, а элементы ее обратной матрицы – через ;

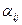2) элементы треугольных матриц В и С обозначим через 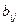и 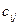соответственно, а элементы обратных матриц – через 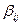и .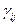

В развернутом виде формула (3.24) запишется так, причем мы рассмотрим только тот случай, когда диагональные элементы матрицы В равны 1.

· =

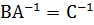
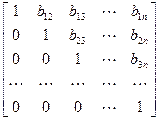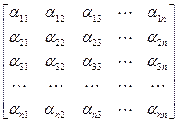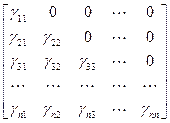
Из этой формулы легко определятся те элементы 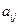, которые стоят в треугольнике над главной диагональю (для них первый индекс i меньше второго индекса j: i < j). Для этого надо использовать правило умножения матриц и условие равенства двух матриц. Например, умножая элементы первой строки матрицы В на соответствующие элементы второго столбца матрицы 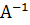и приравнивая сумму произведений нулю – элементу 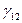в матрице 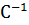, получим

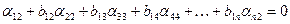
или

,

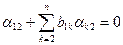откуда

.

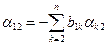Здесь нижний индекс суммирования k = 2есть первый индекс определяемого элемента 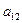, сложенный с 1, т. е. 2 = 1 + 1. Легко установить и общую формулу для определения элементов 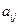при 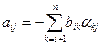i < j

. (i < j).

(3.26)

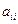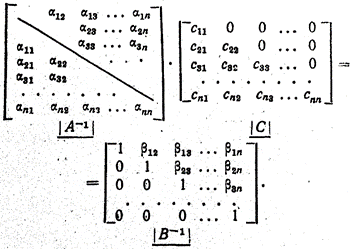
Для определения диагональных элементов и элементов 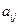, стоящих под главной диагональю (i > j), воспользуемся формулой (3.25)

.

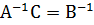Определяемые из этой формулы элементы стоят в треугольнике первого сомножителя. Напомним, что если диагональные элементы треугольной матрицы равны 1, то в обратной для нее матрице диагональные элементы также равны 1 – см. формулу (3.8).

Например, элемент 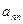определится из произведения элементов последней строки первого сомножителя на соответствующие элементы последнего столбца второго, если сумму этих произведений приравнять на основании условия равенства двух матриц элементу 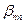матрицы :

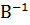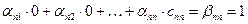
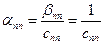
Рассмотрим вычисление какого-либо другого диагонального элемента, например ;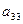

;

;

.

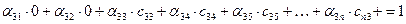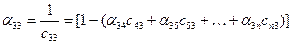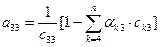(здесь нижний индекс суммирования 4 = 3 + 1, т. е. он равен индексу i определяемого элемента плюс 1) и вообще

,

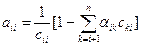(3.27)

а элемент 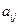, стоящий под главной диагональю (i > j), находят, как легко проверить по формуле

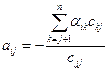. (i > j)

(3.28)

Из формул (3.26) и (3.27) видно, что элементы 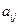обратной матрицы 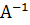выражаются через элементы 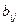и 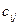тех треугольных матриц, в виде произведения которых представлена данная матрица А, а элементы матриц, обратных треугольным, определять нет надобности. Для удобства выпишем формулы (3.26), (3.27), (3.28), по которым определяются элементы обратной матрицы:

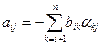; (i < j)

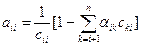; (i = j)

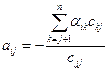; (i > j).

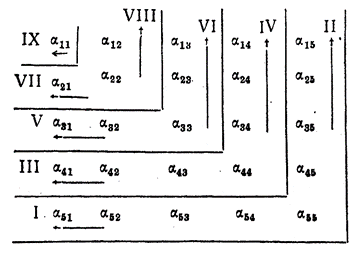В заключение укажем последовательность, в которой следует вести вычисления элементов 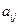, так как между ними существует зависимость, определяемая формулами (3.26) – (3.28), причем эту последовательность укажем применительно к матрице пятого порядка (в качестве примера):

Из этой схемы видно, что сначала следует определить элементы последней строки, начиная тоже с последнего 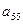, а затем элементы последнего столбца, начиная тоже с последнего, затем – элементы предпоследней строки и предпоследнего столбца, опять-таки начиная с последнего и т. д. Стрелки и римские цифры, проставленные на этой схеме, указывают необходимую последовательность.

На практике обратную матрицу получают, пользуясь такой схемой:

1. Выписывают данную матрицу

2. Под ней образуют две треугольные матрицы, произведение которых равно данной (см. предыдущие задачи).

3. Под этими матрицами по формулам (3.26) – (3.28) получают обратную матрицу данной, соблюдая последовательность определения элементов по указанной схеме.

Задача 3.7 Обратить матрицу

.

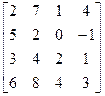Решение.

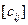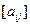			-1
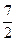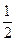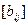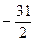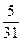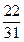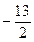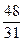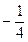	-13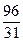
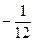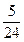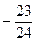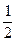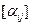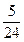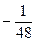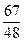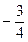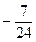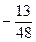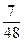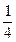		-2

Ниже приведены подробные вычисления элементов 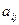обратной матрицы.

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

;

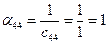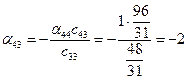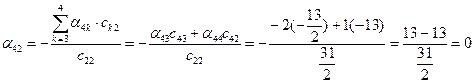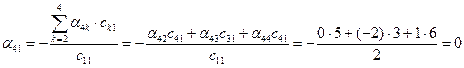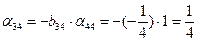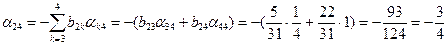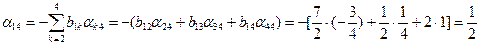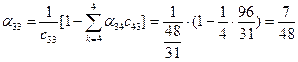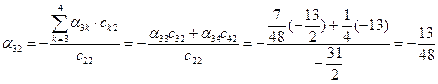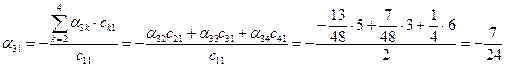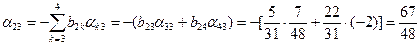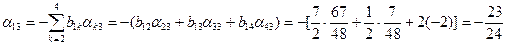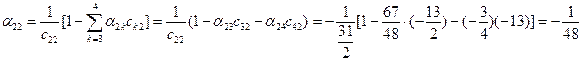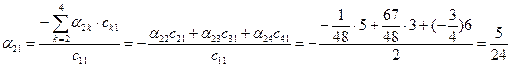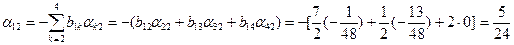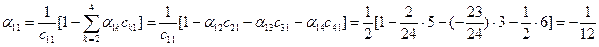Итак, обратная матрица

= = .

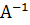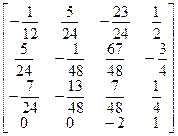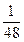
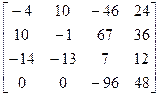Проверка. Должно быть 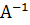· А = Е. Действительно,
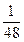
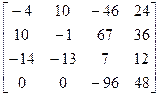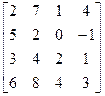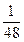
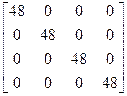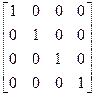· = = =Е.