Как потенциальная энергия деформированной пружины
Лекция
Механические гармонические колебания
Общие сведения о колебаниях.
Дифференциальное уравнение гармонически колебаний.
Решение уравнения гармонических колебаний.
Векторная диаграмма.
Затухающие колебания.
Вынужденные колебания.
Резонанс.
Сложение взаимно-перпендикулярных волн.
Общие сведения о колебаниях
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости (маятник, струна, напряжение между обкладками конденсатора в контуре и другие).
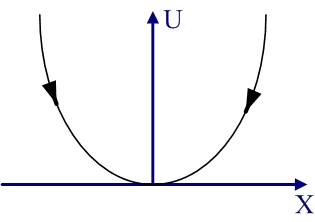
Потенциальная энергия – функция одной переменной:
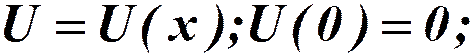
Разложим 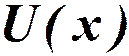 в ряд по степеням
в ряд по степеням 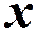 :
:
Формула Макларена:
(ограничимся 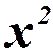 )
)
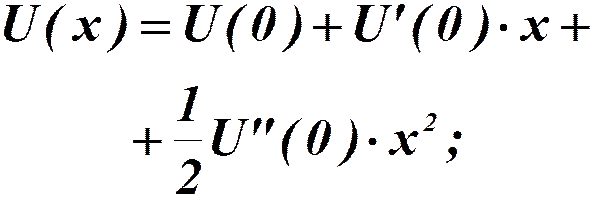
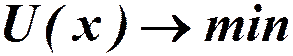 при
при 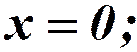
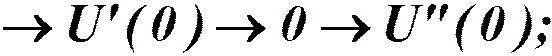
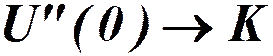
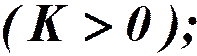

Как потенциальная энергия деформированной пружины.
Сила, действующая на систему:
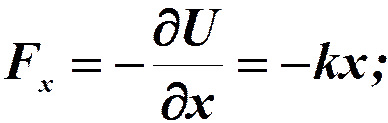
Силы вида 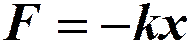 называются квазиупругими. Эта сила всегда направлена к положению равновесия:
называются квазиупругими. Эта сила всегда направлена к положению равновесия:
Свободные колебания
