Динамика установившегося движения неравновесных систем
Неравновесными приводными системами называются такие системы, в которых при сохранении неразрывности кинематической цепи часть элементов при установившемся равномерном движении ведущей массы движется неравномерно, подчиняясь определенному закону, обусловленному кинематическими параметрами.
К неравновесным системам относятся машины, приводы которых содержат кривошипно-шатунный, кривошипно-кулисный или кулачковый механизм, зубчатые передачи с некруглыми колесами, цепные передачи, рычажно-зубчатые механизмы и т.п.
Наиболее типичным механизмом с возвратно-поступательным движением является кривошипно-шатунный (рис. 26).
 При установившейся скорости вала двигателя ведомая масса m2 может быть неподвижной и только после подключения при помощи муфты будет совершать возвратно-поступательное движение.
При установившейся скорости вала двигателя ведомая масса m2 может быть неподвижной и только после подключения при помощи муфты будет совершать возвратно-поступательное движение.
После включения механизма через муфту ведущей массе m1 (не показана) сообщается практически мгновенно некоторая скорость. Если двигатель (асинхронный и некоторые двигатели постоянного тока) имеет жесткую механическую характеристику, то координату x1 можно выразить в виде
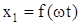 , (207)
, (207)
где 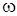 – угловая скорость кривошипа.
– угловая скорость кривошипа.
Уравнение движения ведомой массы будет
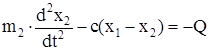 , (208)
, (208)
где Q – внешняя нагрузка (включение механизма в нагруженном состоянии).
Для решения уравнения (208) необходимо знать конкретную функцию 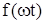 . Для кривошипно-шатунных механизмов, когда отношение длины шатуна L к радиусу кривошипа r достаточно велико, можно принять
. Для кривошипно-шатунных механизмов, когда отношение длины шатуна L к радиусу кривошипа r достаточно велико, можно принять
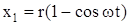 . (209)
. (209)
Подставляя значение x1 в уравнение (208), получим
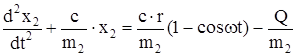 . (210)
. (210)
Общее решение уравнения (210) имеет вид
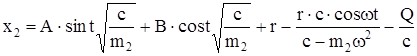 , (211)
, (211)
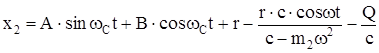 . (212)
. (212)
Начальные условия: при 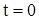
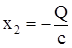 и
и 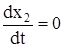 .
.
Тогда
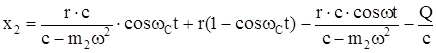 . (213)
. (213)
Деформация шатуна
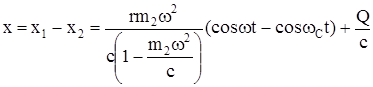 . (214)
. (214)
Величины  и
и 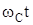 могут принимать любые значения и в том числе такие, при которых одновременно
могут принимать любые значения и в том числе такие, при которых одновременно 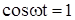 и
и 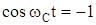 . Кроме того, для системы с достаточно большой жесткостью
. Кроме того, для системы с достаточно большой жесткостью 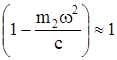 .
.
Тогда усилие 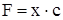 , воспринимаемое штангой, будет иметь максимальное значение
, воспринимаемое штангой, будет иметь максимальное значение
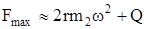 . (215)
. (215)
В случае, когда в момент начала движения шатуна верхний конец его находится в одном из средних положений (кривошип смещен на 90° от горизонтали) и последующее движение шатуна направлено влево (рис. 26), координата 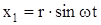 . Подставляя это значение x1 в уравнение (210) и решая при предыдущих начальных условиях, получим
. Подставляя это значение x1 в уравнение (210) и решая при предыдущих начальных условиях, получим
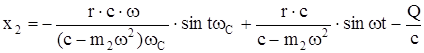 . (216)
. (216)
Деформация упругого звена (шатуна)
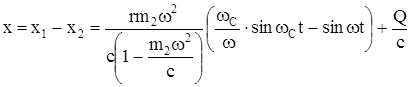 , (217)
, (217)
а воспринимаемое усилие
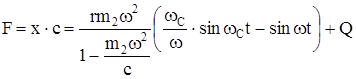 . (218)
. (218)
Максимальная нагрузка равна
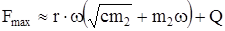 . (219)
. (219)
В случаях, когда начало движения шатуна происходит из остальных двух типичных положений (левое крайнее и смещенное на 90° при последующем движении шатуна вправо – рис. 26),результаты определяются соответственно формулами (215) и (219).
 |
Графики изменения нагрузки шатуна в функции времени показаны на рис. 27 и 28.
