Производная обратной функции
Если функция у = f (х) имеет обратную функцию х = g(x) на интервале (а, b) и имеет отличную от нуля производную у¢х , то обратная функция дифференцируема и производная определяется по формуле:
х¢у = 1/ у¢х.
Таблица производных основных элементарных функций.
| c¢=0, с=const | (ex)¢=ex |
| (xn)¢=nxn-1 | (sin x)¢=cos x |
| (ax)¢=ax ln a | (cos x)¢= -sin x |
(ln x)¢= 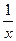 | (tg x)¢= 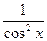 |
(log a x)¢= 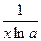 | (ctg x)¢= - 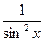 |
(arcsin x)¢= 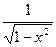 | (arctg x)¢= 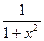 |
(arccos x)¢= - 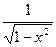 | (arcctg x)¢= - 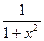 |
Пример 1: К выполнению контрольного задания №2
Найти производную у ¢ и дифференциал функции у = 3х • sin x
Решение:
Здесь используются правила нахождения производной от произведения функций и вынесения множителя за знак производной.
Обозначим :
u =3х, v = sin x
u¢ =3 v¢ =cos x
По формуле (uv)¢ = u ¢v + u v¢, запишем у ¢ = 3 (sin x + x соs x )
Дифференциал функции dy = 3 ( sin x + x cos x) dx.
Производные высших порядков
Производная от функции называется производной первого порядка или первой производной. Производная от первой производной называется производной второго порядки или второй производной, затем – третьей и так далее пока производные высших порядков будут существовать.
Обозначаются производные высших порядков так: у¢, у¢¢, у¢¢¢, …, у(n) и т.д.
Пример 2
Найти производные высших порядков от функции у = х3
Решение
Первая производная : у¢ = 3х2, вторая производная: у¢¢ = 6 х, третья производная: у¢¢¢= 6, четвертая: у(4) = 0 и все остальные производные y(n) равны «0».
4.13. Дифференциалы высших порядков
Дифференциалы высших порядков определяются по формуле:
dn y = f (n) (x) dxn
Приложение второй производной в механике
Пусть материальная точка движется неравномерно по закону S = f(t). Как было показано ранее скорость движения точки в момент времени t определяется по формуле v(t) = S¢ (t). Скорость v(t) также есть функция от времени t. Тогда производная от скорости по времени называется ускорениеми равна:
a = v¢ (t) = S¢¢(t).
Ускорение неравномерного движения материальной точки является второй производной от пути по времени.
Пример 3 для контрольного задания № 2.
Тело движется прямолинейно по закону:
S = 3 – 2t + t3
Найти скорость и ускорение в момент времени t = 3.
Решение
Находим первую производную от пути по времени:
v = S¢ (t) = -2 + 3t2, подставим t = 3, получим v(3)= 25.
Находим вторую производную от пути по времени:
а = S¢¢(t) = 6t, подставим t = 3, получим а(3) = 18.
Ответ: В момент времени t = 3 скорость движения тела равна 25 ед., ускорение движения равно 18 ед.
