Прямая перпендикулярна плоскости, если она

перпендикулярна двум пересекающимся прямым

в этой плоскости. (17)

Точка А принадлежит плоскости, т. к. она принадлежит прямой СD, которая, в свою очередь, принадлежит плоскости (14). Проекции точки принадлежат проекциям прямой.

Те же плоскость, прямая и точка изображены на плоском чертеже рис. 13. Фронтальный след плоскости Q₂ и его фронтальная проекция (Q₂)₂ совпадают. Горизонтальная проекция (Q₂)₁ фронтального следа Q₂ совпадает с осью Х₁₂. Горизонтальная проекция (Q₁)₁ горизонтального следа Q₁ совпадает со следом. Фронтальная проекция (Q₁)₂ совпадает с осью Х₁₂.

Положение плоскости в прямоугольной системе координат определяется положением ее базы A(X, Y, Z) и углами наклона плоскости a, b, g к плоскостям проекций.

Угол a наклона плоскости Q к горизонтальной плоскости проекций П₁ можно определить, если изменить угол наклона плоскости Q к плоскости П₂ до 90°. В этом случае плоскость Q и плоскость П₁ , образующие двугранный угол, будут перпендикулярны третьей плоскости П₂. Согласно правилу измерения двугранного угла (15) он будет определен между линией пересечения плоскости Q c плоскостью П₂ (след плоскости Q¹₂) и линией пересечения плоскости П₁ с плоскостью П₂ (ось Х₁₂).

Плоскость Q будет перпендикулярна плоскости П₂, если любая прямая плоскости Q будет перпендикулярна плоскости П₂ (16). При этом угол a этой прямой равен нулю, например, прямые Q₁ и CD. b^Q1 = Q₁^Ù (Q₁)₂ , где (Q₁)₂ совпадает с Х₁₂, b^CD= CD^Ù С₂D₂.

В положении 1 (рис. 13) вращением вокруг оси iz (см. рис. 3) изменен угол b плоскости Q до 90°. Для чего изменены углы b^Q1 и b^CD от исходного положения до 90° (Q¹₁ ^ Х₁₂ , С¹₁D¹₁ ^ Х₁₂). Определяющее взаимное положение параллельных прямых расстояние е остается неизменным (при a = const сохраняется геометрия горизонтальной проекции).

Фронтальный след плоскости Q¹₂ построен по двум точкам: точка пересечения горизонтального следа Q¹₁ с осью Х (следы пересекаются в точке на оси Х) и фронтальная проекция точки С¹₂ (точка С принадлежит фронтальному следу плоскости и С¹₂ совпадает с С¹). Горизонтальная проекция С¹₁ находится на пересечении горизонтальной проекции прямой СD c осью Х, т. к. Y^C = 0. Фронтальная проекция С¹₂ расположена на пересечении линий связи к оси Х и линии связи к оси Z через С₂.

a^Q = Q¹₂ ^Ù Х₁₂.

Угол b наклона плоскости Q к фронтальной плоскости проекций П₂

можно определить, если изменить угол наклона плоскости Q к плоскости

П₁ до 90°. В этом случае плоскость Q и плоскость П₂ , образующие двугранный угол, будут перпендикулярны третьей плоскости П₁. Угол b^Q будет определен между линией пересечения плоскости Q c плоскостью П₁ и линией пересечения плоскости П₂ с плоскостью П₁.

Пример.Определить параметры плоскости D(АВС) (рис. 14).

Внешние параметры определяют положение объекта в пространстве:

- текущая база БТ(X, Y, Z);

- углы наклона a, b и g к плоскостям проекций (для практических целей достаточно двух углов).

Внутренние параметрыопределяют геометрические размеры объекта. Например, длина прямой, площадь треугольника и т. д. Изменение внутренних параметров приводит к изменению свойств объекта. Например, самолет с изменяемой геометрией крыла.

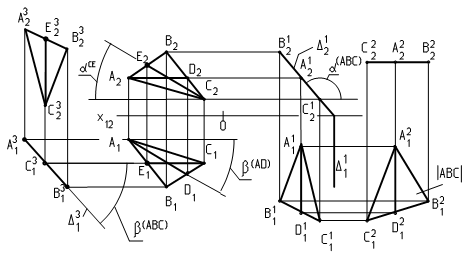Рис. 14. Параметры плоскости.

В исходном положении треугольника АВС(А₁В₁С₁,А₂В₂С₂) определены координаты текущей базы А(Х=÷0l_X÷, Y=÷A₁X₁₂÷,Z=÷A₂X₁₂÷).

Для определения угла наклона a плоскости АВС к горизонтальной плоскости проекций П₁ в первом текущем положении изменен угол b до 90°. Для чего в плоскости АВС взяли прямую AD(A₁D₁,A₂D₂), угол наклона

которой к плоскости П₁ равен 0. Угол наклона b^(AD) к П₂ измерен согласно (6) между (A₁D₁) = ÷AD÷ и (A₂D₂). В первом текущем положении он увеличен до 90°. В результате b^(AВС) согласно (16) равен 90°. С фронтальной проекцией треугольника (A¹₂В¹₂С¹₂) совпадет фронтальный след плоскости D¹₂. Согласно (15) a ^(АВС) = D¹₂(линия пересечения плоскости АВС с П₂) ^Ù Х₁₂(линия пересечения плоскости П₁ с П₂)

Для определения угла наклона b плоскости АВС к фронтальной плоскости проекций П₂ в третьем текущем положении изменен угол a плоскости до 90°. Для чего в плоскости АВС взяли прямую СЕ(С₁Е₁,С₂Е₂), угол наклона которой к плоскости П₂ равен 0. Угол наклона a^(СЕ) к П₁ измерен согласно (6) между (С₂Е₂) = ÷СЕ÷ и (С₁Е₁). В третьем текущем положении он увеличен до 90°. В результате a^(AВС) согласно (16) равен 90°. С горизонтальной проекцией треугольника (A³₁В³₁С³₁) совпадет горизонтальный след плоскости D³₁. Согласно (15) угол наклона b ^(АВС) = D³₁(линия пересечения плоскости АВС с П₁) ^Ù Х₁₂(линия пересечения плоскости П₂ с П₁).

Для определения натуральной величины D(АВС) в текущем положении два угол наклона a ^(АВС) вращением вокруг оси iY (см. рис. 3) изменен до 0. В этом случае горизонтальная проекция треугольника (A²₁В²₁С²₁) = ÷АВС÷. Только в этом положении на плоском чертеже можно менять внутренние геометрические параметры треугольника и выполнять иные геометрические построения в плоскости D (например, определить высоту треугольника, построить вписанную окружность и т. д.).

Взаимное положение точек

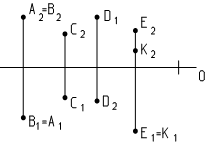Точки могут совпадать или находиться выше, ниже, правее, левее, ближе, дальше по отношению к наблюдателю и друг к другу (рис. 15). Между двумя точками можно измерить расстояние. Для этого следует определить длину отрезка прямой, который задан этими точками. Направление с одной точки на другую будет определено наклона упомянутого отрезка к плоскостям

Рис. 15 проекций.

На рис. 15 точки А и В совпадают, т. к. совпадают их фронтальные проекции А₂=В₂ и горизонтальные проекции А₁=В₁. Точка С находится дальше от наблюдателя и ниже по отношению к точке D (координаты Y и Z точки D больше). Точки Е и К равноудалены от плоскости П₂ (Y^Е= Y^К), но точка Е расположена выше точки К (Z^Е больше Z^К).