Определение перемещений балок при поперечном изгибе
8.9.1. Понятие о перемещениях балки. Дифференциальное уравнение упругой линии балки
Кроме расчетов на прочность для элементов конструкций выполняются расчеты на жесткость. Напомним, что под жесткостью подразумевается такие требования, при которых перемещения (деформации) элементов конструкций не должны превосходить допускаемы величин. Здесь под перемещением подразумевается прогиб балки 𝓌=𝓌(x) в сечении с координатой х и углом поворота сечения 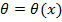 (рис.8.33).
(рис.8.33).
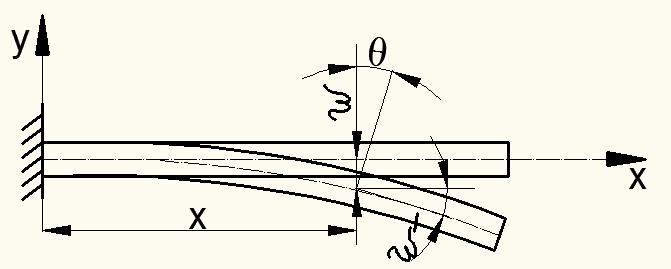
Рисунок 8.33 – Перемещения при изгибе балки
При малых прогибах угол поворота сечения 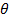 равен углу между касательной к упругой линии в данной точке и осью балки
равен углу между касательной к упругой линии в данной точке и осью балки 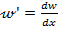 :
:
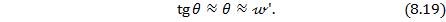
Правило знаков для перемещений: прогиб положителен при перемещении вверх, т.е. в сторону положительной оси у; угол поворота сечения положителен при повороте против часовой стрелки.
Между кривизной упругой линии балки и изгибающим моментом М=М(х) существует зависимость:
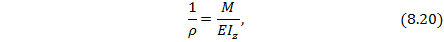
где  – кривизна изогнутой оси балки, которая характеризует величину деформации при изгибе (
– кривизна изогнутой оси балки, которая характеризует величину деформации при изгибе ( 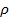 – радиус кривизны);
– радиус кривизны); 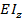 – жесткость при изгибе балки.
– жесткость при изгибе балки.
Заметим, что при ρ>0 кривизна 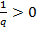 и линия функции 𝓌=𝓌(x) обращена выпуклость вниз, т.е. в сторону положительного значения изгибающих моментов
и линия функции 𝓌=𝓌(x) обращена выпуклость вниз, т.е. в сторону положительного значения изгибающих моментов 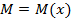 . Отсюда знак кривизны линии совпадает со знаком изгибающего момента.
. Отсюда знак кривизны линии совпадает со знаком изгибающего момента.
Из математики известна зависимость между кривизной линии  и ее функцией 𝓌:
и ее функцией 𝓌:
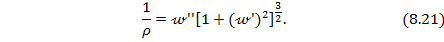
В пределах упругих деформаций материала балки величина 𝓌ʹ составляет тысячные доли радиана, следовательно, можно пренебречь значением (𝓌ʹ)2 по сравнению с единицей, тогда 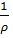 = 𝓌ʹʹ. Подставляя сюда выражение (8.20), получим:
= 𝓌ʹʹ. Подставляя сюда выражение (8.20), получим:
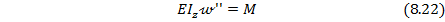
Зависимость (8.22) называется дифференциальным уравнением упругой линии балки. Оно связывает функцию прогиба 𝓌 с одной стороны с уравнением изгибающих моментов М по длине балки с другой стороны.
Интегрированием уравнения (8.22) можно получить величины перемещений при изгибе балки.
8.9.2. Вычисление перемещений путем интегрирования уравнения упругой линии балки
Пусть при поперечном изгибе балки известно аналитическое выражение (уравнение) для изгибающего момента М=М(х). Тогда двукратным интегрированием дифференциального уравнения упругой линии балки (8.22) можно найти выражения для углов поворота сечений по длине балки 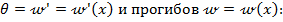
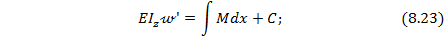
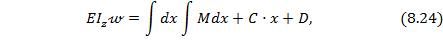
где 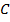 и
и 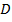 – постоянные интегрирования, которые определяются из граничных условий.
– постоянные интегрирования, которые определяются из граничных условий.
Граничными условиями называются условия опирания балки на крайних опорах. Эти условия представляют собой равенство нулю на опорах прогибов или углов поворота сечений.
Так, для простейших случаев опирания балки на опорах (рис.8.34) граничными условиями будут:
а) при шарнирном опирании балки по концам (рис.8.34, а):
· при 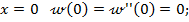
· при 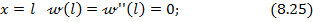
б) при жесткой заделке балки по концам (рис.8.34, б):
· при 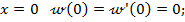
· при 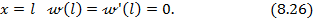
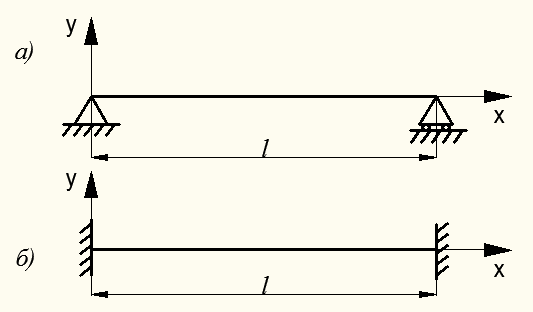
Рисунок 8.34 – Простейшие виды опирания балки на опорах
Рассмотрим вычисление элементов изгиба балок для типичных случаев нагрузки, наиболее часто встречающихся на практике.
Случай 1. Балка, защемленная одним концом, изгибается силой Р, приложенной на другом конце (рис.8.35). Определить прогиб балки на конце консоли 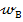 .
.
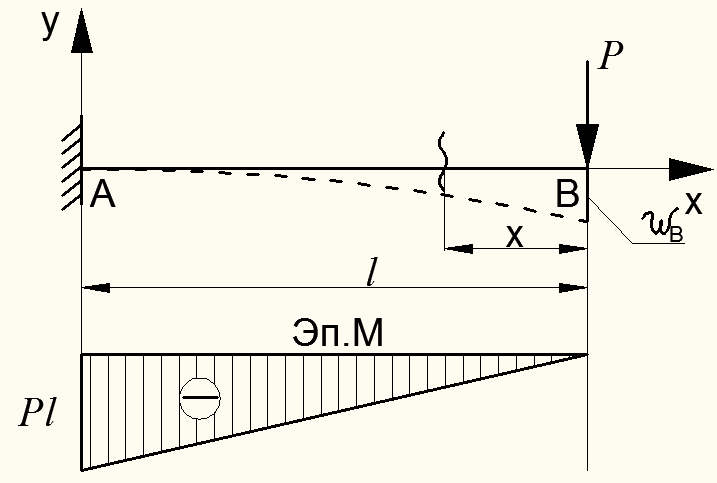
Рисунок 8.35 – Жестко заделанная балка при изгибе от силы Р
Решение
Уравнение изгибающего момента в сечении х:
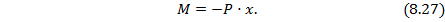
Интегрируя дифференциальное уравнение упругой линии балки (8.22), на основании выражений (8.23) и (8.24) находим:
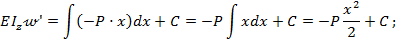
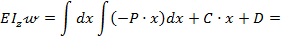
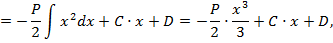
т.е. соответственно:
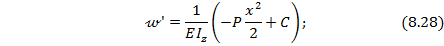
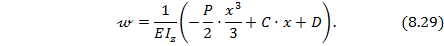
Для определения постоянных интегрирования С и D используем граничные условия (8.26), соответствующие рассматриваемому случаю опирания балки (см. рис. 8.35):
- при 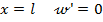 ; из выражения (8.28) находим:
; из выражения (8.28) находим:
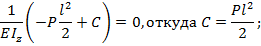
- при 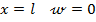 ; из выражения (8.29) находим:
; из выражения (8.29) находим:
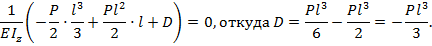
Уравнение прогибов балки на основании выражения (8.29) опишется зависимостью:
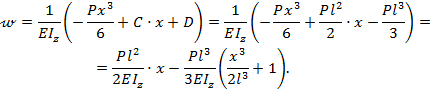
Тогда формула для прогиба балки на конце консоли в т.В при х=0 будет:
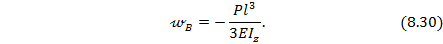
Знак минус в формуле (8.30) соответствует тому, что прогиб т.В направлен в сторону отрицательной оси у, т.е. вниз.
Случай 2. Балка, шарнирно опертая на двух опорах (рис. 9.36), изгибается сплошной равномерно распределенной нагрузкой интенсивности q. Определить угол поворота сечения на опорах и прогиб посредине балки.
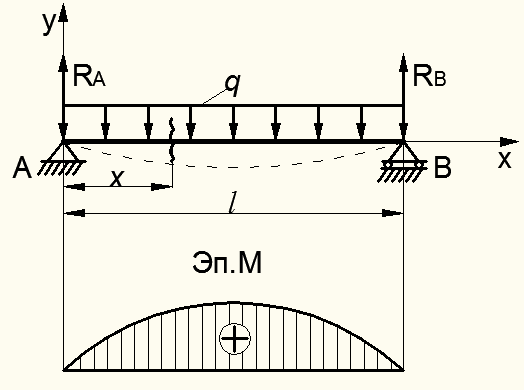
Рисунок 8.36 – Изгиб шарнирно опертой балки при равномерно распределенной нагрузке
Решение
Реакции опор из условий статики равны:
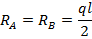
Уравнение для изгибающего момента в сечении х балки:
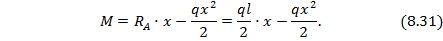
На основании выражений (8.23) и (8.24) с учетом зависимости (8.31) запишем уравнения для углов поворота и прогибов балки по ее длине при заданном виде нагрузки:
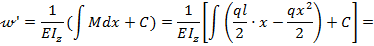
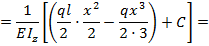
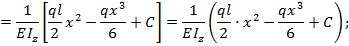
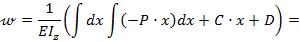
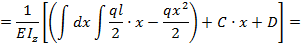
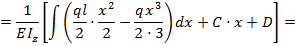
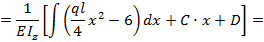
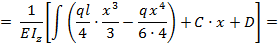
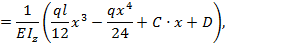
т.е. соответственно:
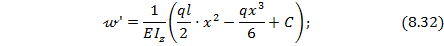
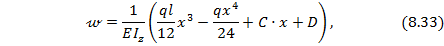
Для определения постоянных интегрирования С и D воспользуемся граничными условиями (8.25):
- при 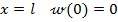 ; из выражения (8.33) находим
; из выражения (8.33) находим 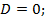
- при 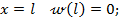 на основании уравнения (8.33) имеем:
на основании уравнения (8.33) имеем:
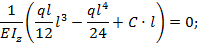
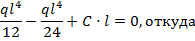
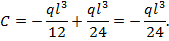
Подставляем найденные значения С и D в выражения (8.32) и (8.33):
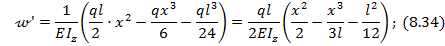
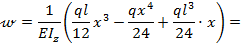
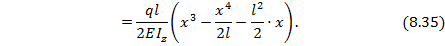
Из окончательно полученного выражения для углов поворота балки по ее длине (8.34) найдем угол поворота левого сечения А при х=0:
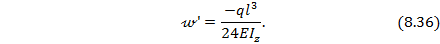
Знак минус в этом выражении показывает, что с учетом принятого правила знаков сечение А балки поворачивается по часовой стрелке.
Из зависимости (8.35) получим выражение для прогиба балки посередине пролета при 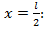
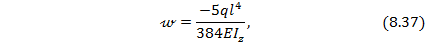
что соответствует прогибу точки балки вниз посредине ее пролета.
Рассмотренный на приведенных примерах метод определения перемещений балки относится к классу аналитических методов, дающих точное решение задач. Однако данный метод не удобен тем, что при нескольких участках нагрузки балки k, а значит разных уравнениях для изгибающих моментов в них, на каждом участке будет по две постоянных интегрирования типа С и D. Тогда общее число постоянных составит ( 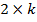 ) и для их определения необходимо решать систему уравнений с большим числом неизвестных. Задача становится громоздкой и неудобной для практики. Однако существует другой подход к определению перемещений балки при нескольких участках нагружения, когда число постоянных в уравнениях упругой линии не будет зависеть от количества участков нагрузки.
) и для их определения необходимо решать систему уравнений с большим числом неизвестных. Задача становится громоздкой и неудобной для практики. Однако существует другой подход к определению перемещений балки при нескольких участках нагружения, когда число постоянных в уравнениях упругой линии не будет зависеть от количества участков нагрузки.
8.9.3. Вычисление перемещений балки на основе метода начальных параметров
Использование нескольких математических приемов (например, интегрирования без раскрытия скобок; введение сомножителей перед нагрузками, учитывающих место их приложения; введение дополнительной распределенной нагрузки) позволило получить обобщенное (для типичных случаев нагрузки), или универсальное уравнение упругой линии балки. Метод расчета перемещений балки на основе универсального уравнения ее упругой линии называется методом начальных параметров.
Рассмотрим практическую сторону использования универсального уравнения упругой линии балки по определению ее перемещений методом начальных параметров.
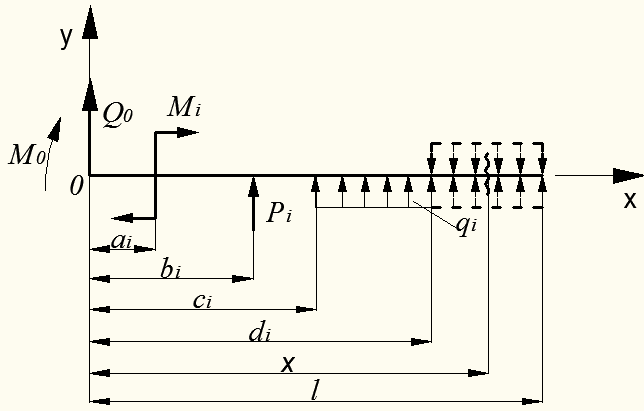
Рисунок 8.37 – Общий случай нагрузки балки основными типами внешних сил
На балку длиной l действует несколько i основных типов внешних сил: моментов Мi, сосредоточенных сил Рi, распределенной нагрузки интенсивности qi (рис.8.37). Начало координат т.О принимается на левом конце балки. Координаты приложения внешних сил, отсчитываемые от т.О, обозначены ai, bi, ci, di. Внешние силы имеют направления, приводящие к положительным изгибающим моментам от их действия в сечении х на последнем участке балки. Если распределенная нагрузка не доходит до конца балки, то ее следует продлить до конца, а чтобы не изменять условия работы балки, следует одновременно приложить нагрузку той же интенсивности и равную добавленной, но обратного знака.
Универсальное уравнение для прогиба балки на последнем участке (см. рис.8.37) имеет вид:
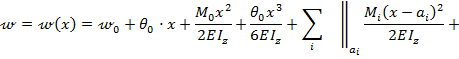
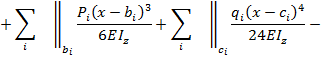
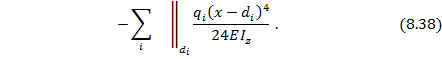
Дифференцируя это уравнение, получаем выражение для углов поворота сечений балки:
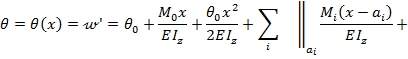
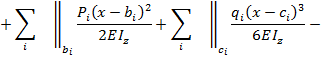
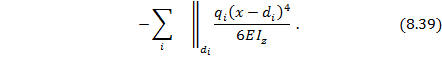
В этих выражениях обозначено: 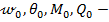 соответственно прогиб, угол поворота сечения, изгибающий момент, перерезывающая сила на левом конце балки, определяемые из граничных условий (эти величины называются начальными параметрами, а отсюда и название метода); знак
соответственно прогиб, угол поворота сечения, изгибающий момент, перерезывающая сила на левом конце балки, определяемые из граничных условий (эти величины называются начальными параметрами, а отсюда и название метода); знак 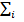 показывает возможность учета нескольких типовых нагрузок; значок
показывает возможность учета нескольких типовых нагрузок; значок 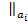 и другие показывает, что соответствующее слагаемые следует учитывать только при
и другие показывает, что соответствующее слагаемые следует учитывать только при 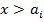 , а при
, а при 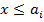 оно равно нулю (это значок называется значком Бубнова или прерывателем Герсиванова).
оно равно нулю (это значок называется значком Бубнова или прерывателем Герсиванова).
Метод начальных параметров также относится к классу аналитических методов вычисления перемещений балки.
8.9.4. Решение типовых задач по определению перемещений балки методом начальных параметров. Задания для индивидуальной работы
Пример 8.9.1. Балка, лежащая на двух шарнирных опорах, изгибается внешним моментом 𝔐, приложенным посредине пролета (рис.8.38). Определить углы поворота сечений над опорами и максимальный прогиб балки.
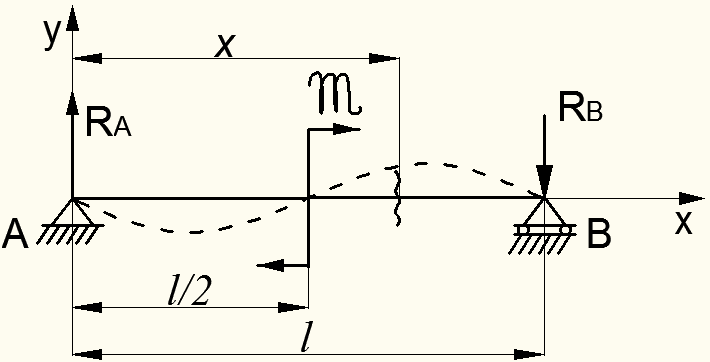
Рисунок 8.38 – К определению перемещений балки от внешнего момента
Решение
Реакции опор балки от заданной нагрузки определяются из условий статики (см.п.8.2, рис.8.8):
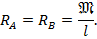
Прогиб балки и углы поворота ее сечений определяются из универсальных уравнений упругой линии балки (8.38) и (8.39). Здесь сразу из вида опор и граничных условий на них находятся начальные параметры: 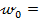
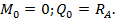 Тогда универсальные уравнения в сечении х для рассматриваемой балки примут вид:
Тогда универсальные уравнения в сечении х для рассматриваемой балки примут вид:
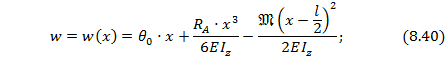
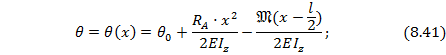
Подчиняя выражение (8.40) граничному условию на первой опоре при 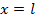 в т.В
в т.В 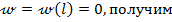
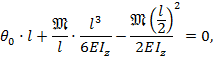
откуда
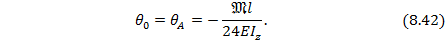
Из-за симметрии приложения внешнего момента 𝔐 по отношению к опорам балки имеем:
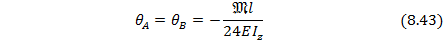
Знак минус в выражении (8.43) свидетельствует о том, что сечение А и В от действия момента 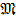 поворачивается по часовой стрелке, а по принятому правилу знаков это соответствует отрицательным углам поворота сечений балки.
поворачивается по часовой стрелке, а по принятому правилу знаков это соответствует отрицательным углам поворота сечений балки.
Все начальные параметры в уравнениях упругой линии балки определены, а отсюда можем вычислить максимальный прогиб балки при заданной нагрузке.
Из условий экстремума функции прогиба 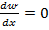 находим то значение х, при котором функция
находим то значение х, при котором функция 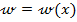 на первом участке получает максимальное значение:
на первом участке получает максимальное значение:
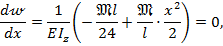
или
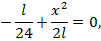
откуда
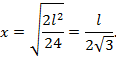
Максимальный прогиб на первом участке найдем, подставив полученное значение х в уравнение прогибов (8.40):
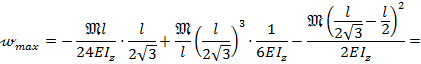

Определим прогиб посредине балки, т.е. при 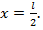 Из уравнения (8.40) получим:
Из уравнения (8.40) получим:
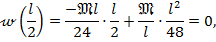
т.е. посредине балки прогиб равен нулю и упругая линия здесь имеет точку перегиба.
На втором участке прогибы будут такие же, как и на первом участке, но противоположные по знаку.
Пример 8.9.2. Определить прогиб балки, изображенной на рис 8.39, в сечениях В и С. Принять значение интенсивности распределенной нагрузки 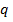 =
= 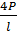 .
.
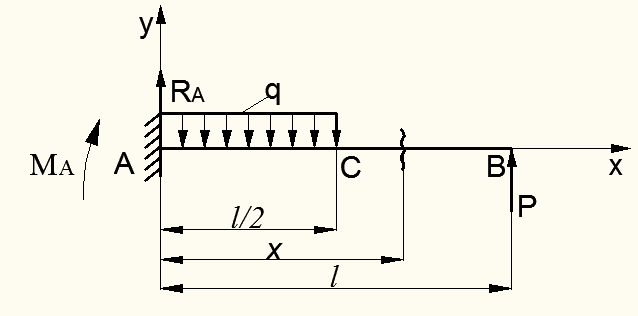
Рисунок 8.39 – К определению перемещений балки от заданной нагрузки
Решение
Реакции балки в защемлении т.А определяются из условий статики и для заданной нагрузки равны:
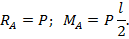
В начале координат начальные параметры равны:
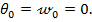
Прогиб балки в сечении т. С, т.е. при 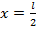 , из уравнения (8.38) будет:
, из уравнения (8.38) будет:
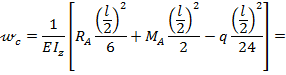
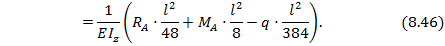
Распределенная нагрузка распространяется до сечения в т. С, поэтому последнее слагаемое уравнения (8.38) обращается в ноль; перед q взят знак минус, так как распределенная нагрузка приводит к отрицательному изгибающему моменту в сечении х. Подставив значения 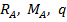 , получим:
, получим:
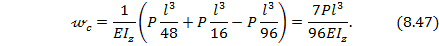
Прогиб в сечении т. В по уравнению (8.38) при 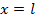 будет:
будет:
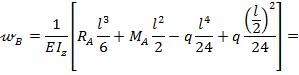
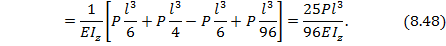
Пример 8.9.3. Определить прогиб и угол поворота сечения в т. С посередине пролета балки (рис.8.40).
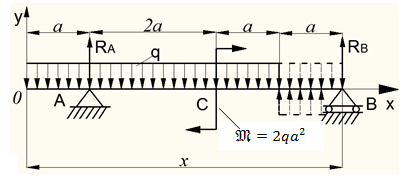
Рисунок 8.40 – К определению перемещений балки от заданной нагрузки
Решение
Реакции на шарнирных опорах определяем из условий статики:
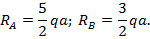
Продлеваем распределенную нагрузку q до т.В и прикладываем на этом участке обратно направленную распределенную нагрузку (см. рис. 8.30). Универсальные уравнения упругой линии балки (8.38) и (8.39) при заданной нагрузке примут вид:
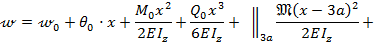
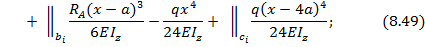

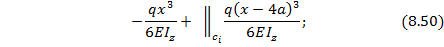
В начале координат т.О при 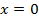 нет сил и моментов, поэтому начальные параметры
нет сил и моментов, поэтому начальные параметры 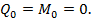 Другие параметры
Другие параметры 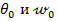 находим из граничных условий:
находим из граничных условий:
- при 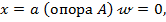 тогда из уравнения (8.49) имеем:
тогда из уравнения (8.49) имеем:
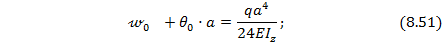
- при 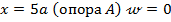 :
:
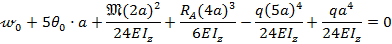
или
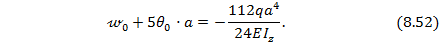
Решая систему уравнений (8.51) и (8.52), находим:
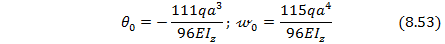
Подставляя полученные значения начальных параметров (8.53) в универсальные уравнения (8.49) и (8.50), посредине пролета балки в т.С при 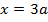 получаем:
получаем:
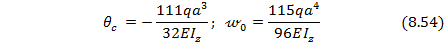
Из данных выражений следует, что т.С посередине пролета балки перемещается вверх, а поперечное сечение в т.С поворачивается по часовой стрелке.
