Нехай на площині задана система координат. Розглянемо рівняння виду
Лекція
Тема: Вектори, дії з векторами
Ціль: Узагальнення шкільних знань студентів по темі «Векторна алгебра», вивчення операцій над векторами.
План:1. Вектор. Координати вектора.
2. Абсолютна величина вектора.
3. Дії над векторами.
4. Скалярний добуток векторів.
5. Векторний добуток векторів.
6. Мішаний добуток векторів.
7. Лінійний векторний простір.
Вектори. Лінійні операції над векторами.
Координати вектора
Відрізок, на якому заданий напрямок, називається вектором. Позначається вектор або символом 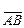 , або однією буквою
, або однією буквою  (рис 1). Відстань між початком і кінцем називається його довжиною або модулем.
(рис 1). Відстань між початком і кінцем називається його довжиною або модулем.
 B
B
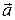
A
Рис. 1
У будь-якій системі координат вектор характеризується своїми координатами 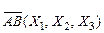 . Якщо в системі координат Oxyz координати початку
. Якщо в системі координат Oxyz координати початку 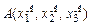 й кінця вектора
й кінця вектора 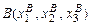 , то координати вектора визначаються формулами:
, то координати вектора визначаються формулами:
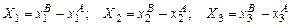 .
.
Модуль вектора 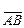 визначається по формулі
визначається по формулі
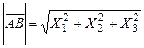 .
.
Два вектори  й
й 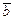 вважаються рівними, якщо вони мають рівні модулі й однакові напрямки:
вважаються рівними, якщо вони мають рівні модулі й однакові напрямки: 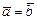 .
.
Алгебраїчною сумою двох векторів 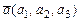 і
і 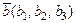 називається новий вектор
називається новий вектор 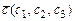 , координати якого
, координати якого
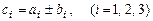 .
.
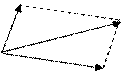
Додавання двох векторів можна робити за правилом паралелограма, коли на векторах  і
і 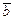 як на сторонах будується паралелограм. Тоді одна з діагоналей буде сумою (мал. 2), а інша різницею векторів
як на сторонах будується паралелограм. Тоді одна з діагоналей буде сумою (мал. 2), а інша різницею векторів  і
і 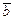 (мал. 3).
(мал. 3).
| 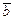  – – 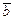  | |||||||||
| Рис. 2 | Рис. 3 |
 х3
х3
М
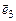
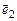 х2
х2
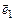
х1
Рис. 4
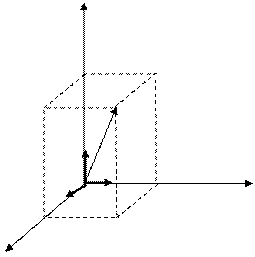
Операція додавання у векторній алгебрі має зворотну дію – розкладання вектора по заданих напрямках, тобто подання його у вигляді суми векторів, паралельних заданим напрямкам. Наприклад, розкладання вектора  по напрямках осей прямокутної декартової системи координат має вигляд (мал. 4)
по напрямках осей прямокутної декартової системи координат має вигляд (мал. 4)
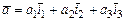 ,
,
де 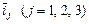 – одиничні вектори (
– одиничні вектори ( 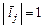 ) або координатні орти, числа
) або координатні орти, числа 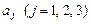 – координати точки М – кінця вектора
– координати точки М – кінця вектора  . Їх називають координатами самого вектора; вони одночасно є й проекціями вектора
. Їх називають координатами самого вектора; вони одночасно є й проекціями вектора  на координатні осі. Вектори
на координатні осі. Вектори 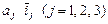 називаються складовими або компонентами вектора
називаються складовими або компонентами вектора  по осях координат. Косинуси кутів, утворених вектором
по осях координат. Косинуси кутів, утворених вектором  з позитивними напрямками осей Ох1, Ох2 і Ох3:
з позитивними напрямками осей Ох1, Ох2 і Ох3: 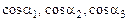 , називають напрямними косинусами вектора
, називають напрямними косинусами вектора  .
.
    Рис. 5 Рис. 5 | Скалярним добутком 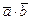 векторів векторів  і і 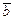 називається число, рівне добутку їхніх модулів на косинус кута j між ними (мал. 5) називається число, рівне добутку їхніх модулів на косинус кута j між ними (мал. 5) 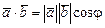 . . |
Скалярний добуток векторів, заданих у координатній формі
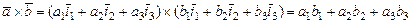 .
.
Кут між векторами
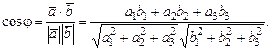
Умова перпендикулярності двох векторів  і
і 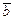
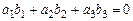 .
.
Умова коллінеарності двох векторів  і
і 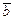
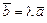 або
або 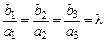 ,
,
тобто однойменні координати повинні бути пропорційні.
Векторним добутком вектора  на вектор
на вектор 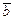 називається вектор
називається вектор 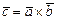 , обумовлений умовами:
, обумовлений умовами:
1) 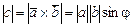 , де j – кут між векторами;
, де j – кут між векторами;
2) 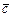 перпендикулярний обом векторам
перпендикулярний обом векторам  і
і 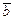 ;
;
3) вектора 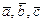 повинні утворювати праву трійку;
повинні утворювати праву трійку;
Векторний добуток векторів, заданих у координатній формі, може бути представлене у вигляді визначника
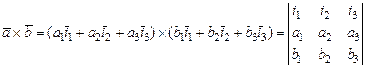 .
.
Мішаним добутком трьох векторів 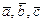 називається добуток виду
називається добуток виду 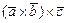 . Чисельно мішаний добуток трьох неколлінеарних (не лежачих в одній площині) векторів дорівнює об'єму паралелепіпеда, побудованого на цих векторах як на сторонах.
. Чисельно мішаний добуток трьох неколлінеарних (не лежачих в одній площині) векторів дорівнює об'єму паралелепіпеда, побудованого на цих векторах як на сторонах.
Якщо перемножуються векторы, що, задані в координатній формі, то їхній мішаний добуток дорівнює визначнику
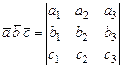 .
.
Лінійний векторний простір
Приведемо узагальнення понять, викладених у попередньому параграфі, на п-мірний випадок.
Будь-який упорядкований набір з п дійсних чисел 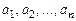 називається п-мірним вектором
називається п-мірним вектором  ; числа, що входять у набір називаються координатами (компонентами) вектора
; числа, що входять у набір називаються координатами (компонентами) вектора  .
.
Сукупність всіх п-мірних векторів, операції над якими мають властивості лінійності, називається п-мірним векторним простором.
Розглянемо систему k векторів
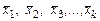 (2.1)
(2.1)
з п-мірного простору. Припустимо, що п-мірний вектор 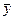 лінійно виражається через вектори системи (2.1), тобто
лінійно виражається через вектори системи (2.1), тобто
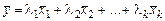 , (2.2)
, (2.2)
де 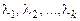 – будь-які дійсні числа.
– будь-які дійсні числа.
У цьому випадку говорять, що вектор 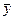 розкладається по векторах
розкладається по векторах 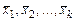 системи (2.1) або, інакше, є лінійною комбінацією векторів системи (2.1).
системи (2.1) або, інакше, є лінійною комбінацією векторів системи (2.1).
Система векторів 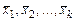 називається лінійно залежної, якщо існує рівна нулю лінійна комбінація
називається лінійно залежної, якщо існує рівна нулю лінійна комбінація
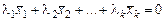 цих векторів, у якій хоча б один з коефіцієнтів
цих векторів, у якій хоча б один з коефіцієнтів 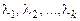 відмінний від нуля. Якщо ж остання рівність для даної системи векторів (2.1) виконується тільки при одночасній рівності нулю всіх
відмінний від нуля. Якщо ж остання рівність для даної системи векторів (2.1) виконується тільки при одночасній рівності нулю всіх 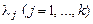 , то ця система векторів називається линійнонезалежною.
, то ця система векторів називається линійнонезалежною.
Система з п векторів п-мірного векторного простору лінійно незалежна тоді й тільки тоді, коли визначник, складений з координат цих векторів, відмінний від нуля.
Набір будь-яких п лінійно незалежних векторів п-мірного векторного простору називається базисом цього простору.
Припустимо, що набір векторів 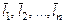 утворить базис п-мірного векторного простору, тоді довільний вектор
утворить базис п-мірного векторного простору, тоді довільний вектор 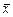 цього простору розкладається, і притім єдиним образом, по векторах базису
цього простору розкладається, і притім єдиним образом, по векторах базису
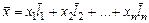 . (2.3)
. (2.3)
Числа 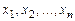 , що беруть участь у розкладанні вектора
, що беруть участь у розкладанні вектора 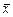 по базисі
по базисі 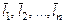 , називаються координатами цього вектора в даному базисі.
, називаються координатами цього вектора в даному базисі.
Взагалі, той самий вектор у різних базисах має різні координати.
Важливе значення має теорема: якщо 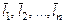 – система лінійно незалежних векторів простору R і будь-який вектор
– система лінійно незалежних векторів простору R і будь-який вектор  лінійно виражається через
лінійно виражається через 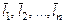 , той простір R є п-мірним, а вектори
, той простір R є п-мірним, а вектори 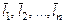 – його базисом.
– його базисом.
Приклади:
1.Є три вектори 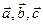 , які задовільнюють умові
, які задовільнюють умові 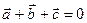 . Відомо, що
. Відомо, що 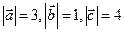 . Обчислити
. Обчислити 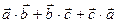
2.Обчислити кут між векторами a=3p+2q, b=p+5q, де p,q - одиничні взаємно перпендикулярні вектори.
Завдання для перевірки знань:
1. Як визначити координати вектора?
2. Як знайти абсолютну величину вектора?
3. Дії над векторами.
4. Скалярний добуток векторів.
5. Векторний добуток векторів.
6. Мішаний добуток векторів.
7. Перевірити, що чотири точки A(3,-1,2), B(1,2,-1), C(-1,1,-3), D(3,-5,3) є вершинами трапеції.
8. На осі ординат знайти точку, рівновіддалену від точок A(1,-3,7), B(5,7,-5).
Література:
1. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.63-82
2. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.82-110
3. «Збірник задач з лінійної алгебри та аналітичної геометрії» за редакцією Ю.К. Руданського стр.45-77
4. Е.Х. Назієв, В.М. Владіміров стр.86-91
Додаткова література:
1. А.Д. Мышкис «Лекции по высшей математике» стр.93-108
2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 96-113
Розділ: «Аналітична геометрія»
Лекція
Тема:Лінія та пряма на площині. Лінії другого порядку.
Ціль: Вивчити зі студентами основні формули по даній темі, а також навчитися вирішувати типові задачі.
План: 1.Рівняння прямої на площині.
2. Кут між прямими.
3. Відстань від точки до прямої.
4. Рівняння еліпса.
5. Рівняння гіперболи.
6. Рівняння параболи.
Елементи аналітичної геометрії на площині
Нехай на площині задана система координат. Розглянемо рівняння виду
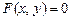 .
.
Це рівність, що зв'язує поточні координати x, y і постійні величини (параметри), визначає деяку криву і є її рівнянням. Особливістю цього рівняння є те, що координати всякої точки, що належить цій кривій, задовольняють рівнянню, а координати будь-якої точки, що не належить кривій, цьому рівнянню не задовольняють.
Лінії на координатній площині можуть бути всілякими.
Лінії першого порядку. До них належать лінії, алгебраїчне рівняння яких 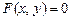 є рівнянням першого ступеня. Ці лінії називаються прямими, і залежно від параметрів, що визначають положення прямої на площині, є кілька видів рівняння прямій, використовуваних у різних задачах.
є рівнянням першого ступеня. Ці лінії називаються прямими, і залежно від параметрів, що визначають положення прямої на площині, є кілька видів рівняння прямій, використовуваних у різних задачах.
Рівняння прямої з кутовим коефіцієнтом
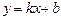 . (1)
. (1)
Тут 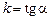 – кутовий коефіцієнт прямої; b – відрізок, що відтинається прямій на осі ординат, як показано на мал. 1.
– кутовий коефіцієнт прямої; b – відрізок, що відтинається прямій на осі ординат, як показано на мал. 1.
Рівняння прямої, що проходить через точку в заданому напрямку (мал. 2)
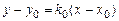 . (2)
. (2)
Рівняння прямої, що проходить через дві задані точки (мал. 3)
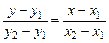 . (3)
. (3)
Рівняння прямої у відрізках (мал. 4) 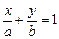 . (4)
. (4)
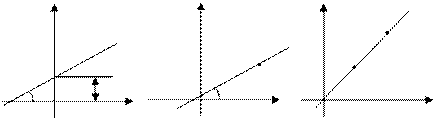 у у 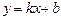 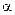 b ПРО х b ПРО х | у М(х0, в0) k0 ПРО х | у М2 (х2, в2) М1(х1, в1) ПРО х | |
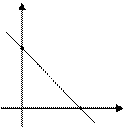 Рис. 1 Рис. 1 | Рис. 2 | Рис. 3 | |
| у М2 (0, b) b М1 (а, 0) О а х | |||
| Рис. 4 | |||
Всі наведені вище рівняння є рівняннями першого ступеня щодо поточних координат x і y. Можна показати, що всяке рівняння першого ступеня
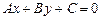 (5)
(5)
буде рівнянням деякої прямої на площині. Це рівняння називають загальним рівнянням прямої.
Кут між прямими.
Розглянемо дві прямі, задані рівняннями 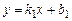 й
й 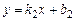 , де
, де 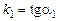 й
й 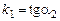 (мал. 4). Нехай ( - кут між цими прямими.
(мал. 4). Нехай ( - кут між цими прямими.
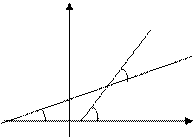 у у 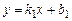 k k 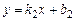 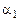 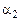 ПРО х ПРО х | Тоді 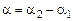 й й 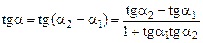 або або 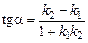 . . |
| Рис. 5 |
З рівності (4) випливають умови: паралельності 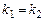 й перпендикулярності
й перпендикулярності 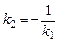 прямих.
прямих.
Відстань від точки до прямої. Нехай пряма задана загальним рівнянням (3). Тоді відстань d від довільної точки 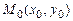 до прямої задається формулою
до прямої задається формулою
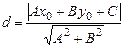 .
.
Лінії другого порядку. До них ставляться еліпс, часткою случаємо якого є окружність, гіпербола й парабола.
Еліпсом (мал. 6) називається геометричне місце крапок площини, сума відстаней від яких до двох точок цієї ж площини, називаних фокусами, постійна.
Канонічне (найпростіше) рівняння еліпса має вигляд
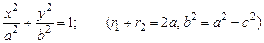 . (6)
. (6)
          у b M(х,у) r1 r2 -а F1(-c,0) ПРО F2(c,0) а х -b Рис. 6 у b M(х,у) r1 r2 -а F1(-c,0) ПРО F2(c,0) а х -b Рис. 6 |
Форма еліпса визначається величиною його ексцентриситету
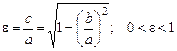 .
.
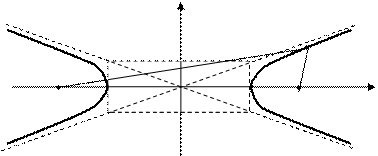
Гіперболою (мал. 7) називається геометричне місце крапок площини, різниця відстаней від яких до двох даних точок тої ж площини, називаних фокусами, постійна.
Канонічне рівняння гіперболи
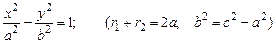 .
.
Ексцентриситет гіперболи
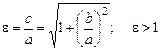 .
.
 у
у
M(х,у)
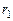
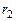
F1 ПРО F2 х
Рис. 7
Параболою (мал. 8) називається геометричне місце точок площини, відстані від яких до заданих на тій же площині точки (фокуса параболи) і прямій (директриси параболи) рівні між собою: 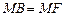 .
.
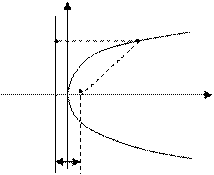 у B М(х,у) D ПРО F х р Рис. 8 у B М(х,у) D ПРО F х р Рис. 8 | Канонічне рівняння параболи 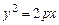 , р – параметр параболи, рівняння директриси , р – параметр параболи, рівняння директриси 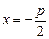 . . |
Помітимо, що та сама крива має різні рівняння при різному її розташуванні на координатній площині: характерні властивості при цьому залишаються колишніми, а міняються тільки властивості положення. Таким чином, усякої лінії на площині із заданою координатною системою відповідає деяке рівняння.
У зв'язку із цим в аналітичній геометрії виникають дві основні задачі. Перша: знаючи геометричні властивості кривої, знайти її рівняння; друга: знаючи рівняння кривої, одержати її властивості й форму.
Завдання для перевірки знань:
1.Рівняння прямої на площині.
2. Кут між прямими.
3. Відстань від точки до прямої.
4. Рівняння еліпса.
5. Рівняння гіперболи.
6. Рівняння параболи.
7.Сторони трикутника лежать на прямих х+5у=7, 3х-2у-4=0, 7х+у+19=0.
Обчислити його площу S.
8. Даний еліпс 9x2+5y2=45. Знайти 1) його півосі; 2) фокуси; 3)ексцентриситет
Література:
5. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.104-115
6. «Збірник задач з лінійної алгебри та аналітичної геометрії» за редакцією Ю.К. Руданського стр.109-121
7. Е.Х. Назієв, В.М. Владіміров стр.103-106
Додаткова література:
1. А.Д. Мышкис «Лекции по высшей математике» стр.262-266
Розділ: «Аналітична геометрія»
Лекція
Тема: Площина та пряма в просторі
Ціль: Вивчити зі студентами основні формули по даній темі, а також навчитися вирішувати типові задачі.
План: 1. Рівняння площини в просторі
2. Кут між площинами
3. Умова перпендикулярності й паралельності площин
4. Рівняння прямої в просторі
5. Кут між прямими в просторі
Поняття про рівняння площини й прямій у просторі. Взаємне розташування прямих, площин, прямій і площині
Нехай у прямокутній системі координат Oxyz координати x, y і z зв'язані деяким рівнянням
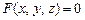 . (1)
. (1)
Співвідношення (1) є рівнянням поверхні S у заданій системі координат, якщо йому задовольняють координати будь-якої точки 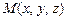 , що належить S, і не задовольняють координати ніякої точки, що не лежить на цій поверхні.
, що належить S, і не задовольняють координати ніякої точки, що не лежить на цій поверхні.
Криву в просторі можна задати як лінію перетинання двох поверхонь, тобто у вигляді системи двох рівнянь виду (1)
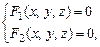 (2)
(2)
кожне з яких окремо визначає одну з поверхонь. Систему (2) називають рівнянням лінії в просторі.
Рівняння виду
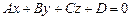 (3)
(3)
називається загальним рівнянням площини в системі координат Oxyz. Вектор 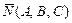 , перпендикулярний цієї площини, називається її нормальним вектором.
, перпендикулярний цієї площини, називається її нормальним вектором.
Площина, що проходить через точку 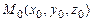 перпендикулярно вектору
перпендикулярно вектору 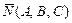 , задається рівнянням
, задається рівнянням
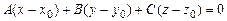 . (4)
. (4)
Кут j між площинами 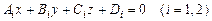 дорівнює куту між їхніми нормальними векторами
дорівнює куту між їхніми нормальними векторами 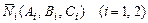
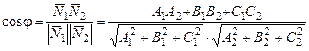 . (5)
. (5)
Умова перпендикулярності площин рівносильно умові перпендикулярності їхніх нормальних векторів
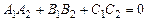 . (6)
. (6)
Умова паралельності площин означає умова коллінеарності їхніх нормальних векторів
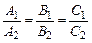 . (7)
. (7)
Пряму в просторі можна розглядати як лінію перетинання двох площин і задавати її системою двох рівнянь першого порядку виду (3); у цьому випадку рівняння називаються загальними рівняннями прямої.
Досить часто вживаються інші типи рівнянь прямій. Положення прямої в просторі можна визначити, задавши деяку крапку 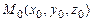 й напрямний вектор
й напрямний вектор 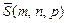 , паралельний даній прямій або лежачий на ній (мал. 1).
, паралельний даній прямій або лежачий на ній (мал. 1).
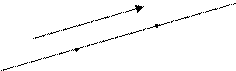 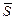 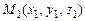 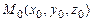 Рис. 1 Рис. 1 | Оскільки вектори 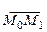 й й 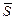 коллінеарні, те з умови їх коллінеарності одержуємо канонічне рівняння прямої в просторі коллінеарні, те з умови їх коллінеарності одержуємо канонічне рівняння прямої в просторі |
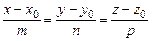 . (8)
. (8)
Увівши деякий скалярний параметр l, одержимо з (8) параметричні рівняння прямої
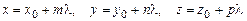 . (9)
. (9)
Кут між прямими, умови їхньої перпендикулярності й паралельності визначаються як відповідні умови для їхніх напрямних векторів.
Нехай пряма й площина задані відповідно рівняннями
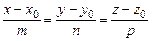 ,
,
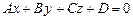 .
.
Тоді кут a між ними визначається як додатковий кут до кута між їх напрямними 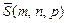 й нормальним
й нормальним 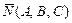 векторами (мал. 2)
векторами (мал. 2)
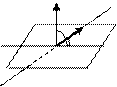 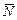 b b 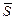 ( Рис. 2 ( Рис. 2 | 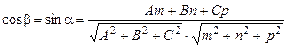 . (10) Зі співвідношення (2.20) одержуємо умову паралельності прямій і площині . (10) Зі співвідношення (2.20) одержуємо умову паралельності прямій і площині 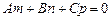 . (11) . (11) |
Пряма перпендикулярна площини, якщо її напрямний вектор 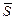 коллінеарний нормальному вектору площини
коллінеарний нормальному вектору площини 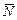 . Звідси умова перпендикулярності прямій і площині
. Звідси умова перпендикулярності прямій і площині
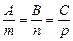 . (12)
. (12)
Завдання для перевірки знань:
1. Рівняння площини в просторі
2. Кут між площинами
3. Умова перпендикулярності й паралельності площин
4. Рівняння прямої в просторі
5. Кут між прямими в просторі
Література:
1. «Збірник задач з лінійної алгебри та аналітичної геометрії» за редакцією Ю.К. Руданського стр.129-142
2. Е.Х. Назієв, В.М. Владіміров стр.91-94