Тема 4.4 Линейные дифференциальные уравнения второго порядка
1 Укажите решение дифференциального уравнения 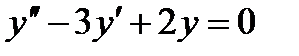 …
…
- а) 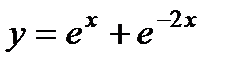
- б) 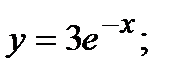
- в) 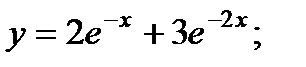
+ г) 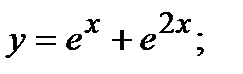
- д) 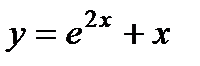
2 Укажите решение дифференциального уравнения 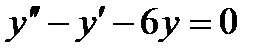 …
…
- а) 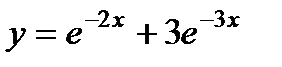
- б) 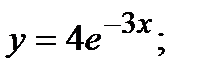
+ в) 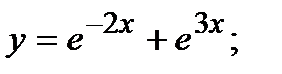
- г) 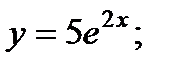
- д) 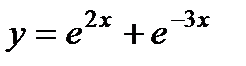 .
.
3 Укажите решение дифференциального уравнения 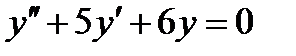 …
…
+ а) 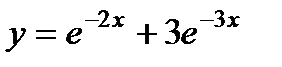
- б) 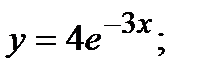
- в) 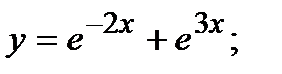
- г) 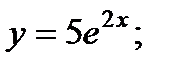
- д) 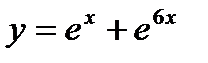 .
.
4 Укажите решение дифференциального уравнения 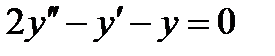 …
…
- а) 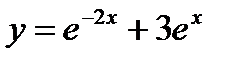
- б) 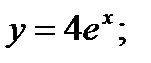
+ в) 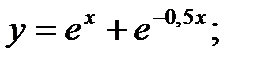
- г) 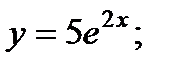
- д) 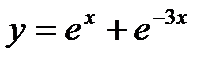 .
.
5 Укажите решение дифференциального уравнения 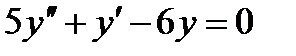 …
…
- а) 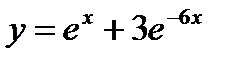
- б) 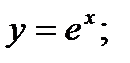
+ в) 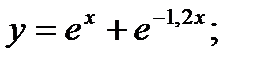
- г) 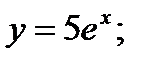
- д) 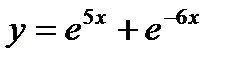 .
.
6 Общее решение дифференциального уравнения 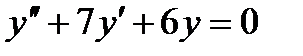 имеет вид
имеет вид
+ а) 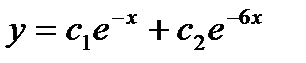
- б) 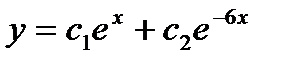
- в) 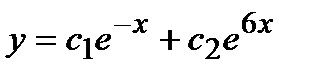
- г) 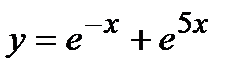
- д) 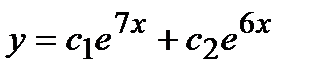
7 Общее решение дифференциального уравнения 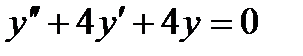 имеет вид
имеет вид
- а) 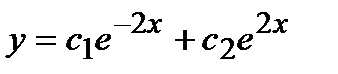
- б) 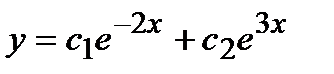
- в) 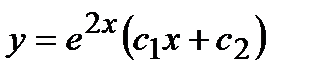
+ г) 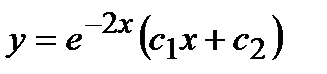
- д) 
8 Общее решение дифференциального уравнения 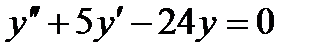 имеет вид
имеет вид
- а) 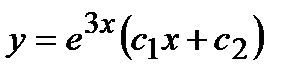
+ б) 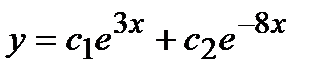
- в) 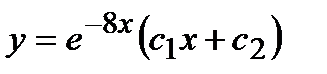
- г) 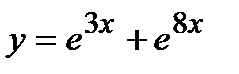
- д) 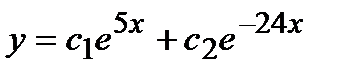
9 Общее решение дифференциального уравнения 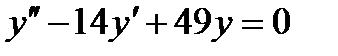 имеет вид
имеет вид
+ а) 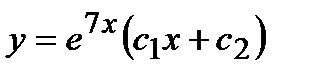
- б) 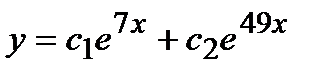
- в) 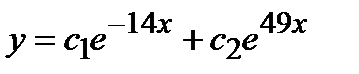
- г) 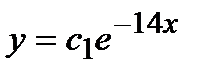
- д) 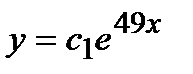
10 Общее решение дифференциального уравнения 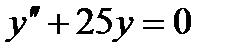 имеет вид
имеет вид
+ а) 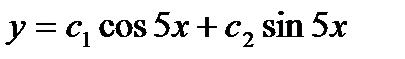
- б) 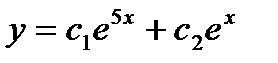
- в) 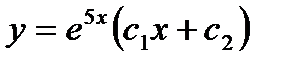
- г) 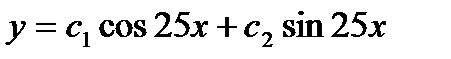
- д) 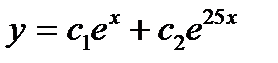
11 Частное решение неоднородного дифференциального уравнения второго порядка 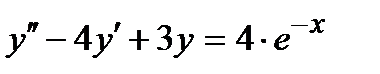 имеет вид…
имеет вид…
+ а) 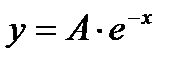
- б) 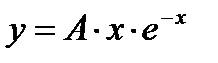
- в) 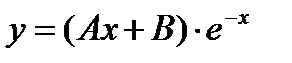
- г) 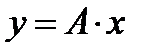
- д) 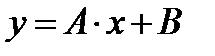
12 Частное решение неоднородного дифференциального уравнения второго порядка 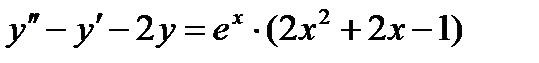 имеет вид…
имеет вид…
+ а) 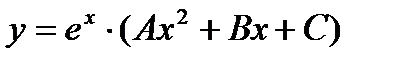
- б) 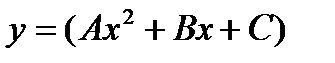
- в) 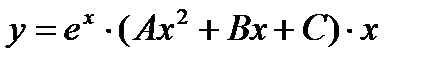
- г) 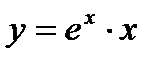
- д) 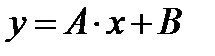
13 Частное решение неоднородного дифференциального уравнения второго порядка 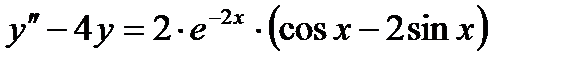 имеет вид…
имеет вид…
- а) 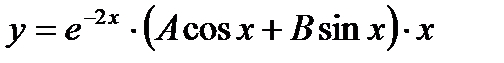
+ б) 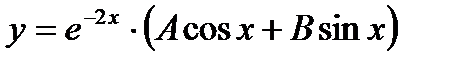
- в) 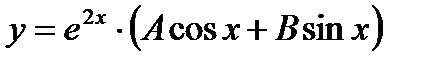
- г) 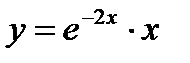
- д) 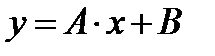
14 Частное решение неоднородного дифференциального уравнения второго порядка 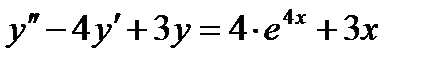 имеет вид…
имеет вид…
+ а) 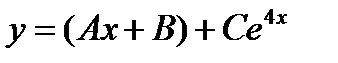
- б) 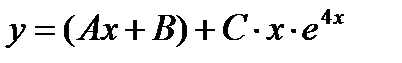
- в) 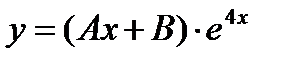
- г) 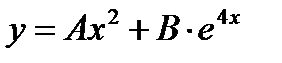
- д) 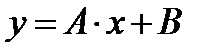
15 Частное решение неоднородного дифференциального уравнения второго порядка 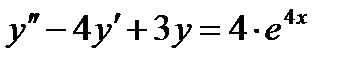 имеет вид…
имеет вид…
+ а) 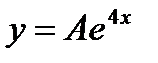
- б) 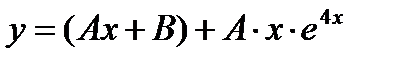
- в) 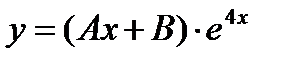
- г) 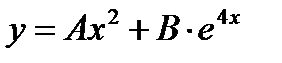
- д) 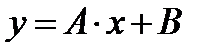
16 Для дифференциального уравнения 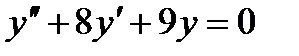 характеристическое уравнение имеет вид…
характеристическое уравнение имеет вид…
- а) 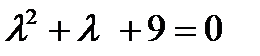
+ б) 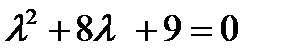
- в) 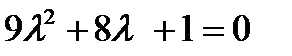
- г) 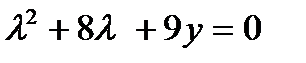
17 Для дифференциального уравнения 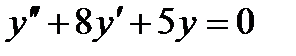 характеристическое уравнение имеет вид…
характеристическое уравнение имеет вид…
- а) 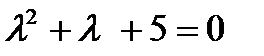
+ б) 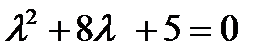
- в) 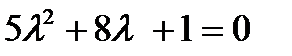
- г) 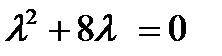
18 Для дифференциального уравнения 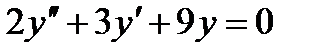 характеристическое уравнение имеет вид…
характеристическое уравнение имеет вид…
- а) 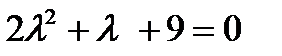
+ б) 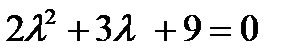
- в) 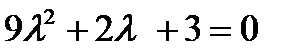
- г) 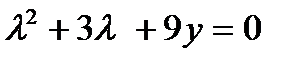
19 Для дифференциального уравнения 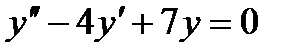 характеристическое уравнение имеет вид…
характеристическое уравнение имеет вид…
+ а) 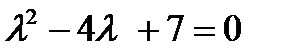
- б) 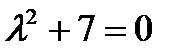
- в) 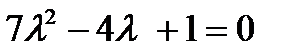
- г) 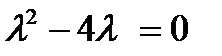
20 Для дифференциального уравнения 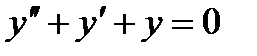 характеристическое уравнение имеет вид…
характеристическое уравнение имеет вид…
- а) 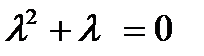
+ б) 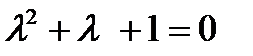
- в) 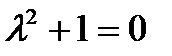
- г) 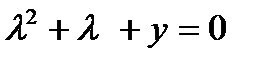
21 Уравнение вида 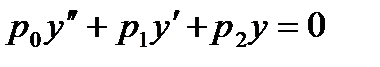 , где
, где 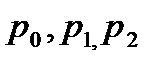 -постоянные, решают..
-постоянные, решают..
- понижением порядка
- с помощью дифференцирования
+ с помощью характеристического уравнения
- подстановкой 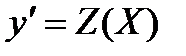
- с помощью интегрирования
22 Уравнение вида 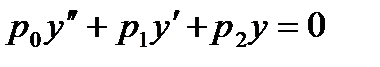 , где
, где 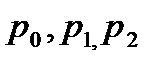 -постоянные, называют
-постоянные, называют
- дифференциальное уравнение второго порядка, допускающее понижение порядка
+однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
- неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
-уравнение Бернулли
-Уравнение Лагранжа
23 Уравнение вида 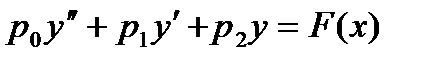 , где
, где 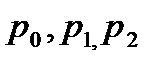 -постоянные, называют
-постоянные, называют
- дифференциальное уравнение второго порядка, допускающее понижение порядка
-однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
+неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
-уравнение Бернулли
-Уравнение Лагранжа
