БИЛЕТ №4
Потенциал. Из независимости от траектории интеграла 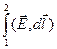 следует, что его можно представить, как убыль некоторой функции координат:
следует, что его можно представить, как убыль некоторой функции координат:
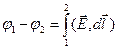 , или (19)
, или (19)
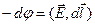 . (20)
. (20)
Введенная таким образом функция координат φ( 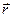 ) называется потенциалом. Разность потенциалов
) называется потенциалом. Разность потенциалов 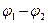 численно равна работе по переносу единичного положительного заряда из точки 1 в точку 2. Из того, что поле способно совершить такую работу, следует, что в точках 1 и 2 заряд обладает различной потенциальной энергией. Поэтому потенциал можно определить как потенциальную энергию пробного заряда q, отнесенную к его величине (правда саму потенциальную энергию всё равно придется вводить через ту же работу):
численно равна работе по переносу единичного положительного заряда из точки 1 в точку 2. Из того, что поле способно совершить такую работу, следует, что в точках 1 и 2 заряд обладает различной потенциальной энергией. Поэтому потенциал можно определить как потенциальную энергию пробного заряда q, отнесенную к его величине (правда саму потенциальную энергию всё равно придется вводить через ту же работу):  . (21)
. (21)
Кроме того, из введенных определений (19,20), а также определения самой потенциальной энергии, следует, что потенциал определен с точностью до константы.
Потенциал поля точечного заряда. Поскольку заряд q создает поле с напряженностью (3), скалярное произведение в формуле (20) можно преобразовать:
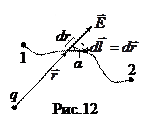
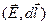 =
= 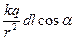 =
= 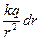 =-
=- 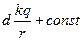 , Þ
, Þ
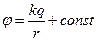 , где
, где 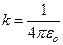 ,
,
и учтено, что 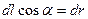 (геометрия – на рис.12). Обычно полагают потенциал при r®¥ равным нулю, тогда
(геометрия – на рис.12). Обычно полагают потенциал при r®¥ равным нулю, тогда 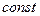 =0. В этом случае потенциал поля точечного заряда выражается формулой
=0. В этом случае потенциал поля точечного заряда выражается формулой
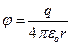 . (22)
. (22)
Если заряды распределены непрерывно с объемной плотностью ρ( 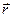 ), то точечным следует считать заряд
), то точечным следует считать заряд 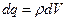 . Тогда потенциал можно представить интегралом по объему
. Тогда потенциал можно представить интегралом по объему
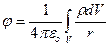 . (23)
. (23)
Аналогично, если заряды распределены по поверхности или линии, то интегрируют по поверхности или линии соответственно
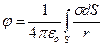 ,
, 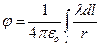 . (24)
. (24)
Единицей потенциала является вольт [φ] = [В].
Связь напряженности и потенциала. Пусть 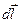 - вектор малого перемещения вдоль траектории. Это значит, что радиус-вектор
- вектор малого перемещения вдоль траектории. Это значит, что радиус-вектор 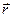 (x,y,z) получил приращение
(x,y,z) получил приращение 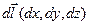 . Тогда
. Тогда
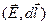 =
= 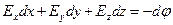 , (25)
, (25)


 откуда следует, что
откуда следует, что 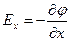 ,
, 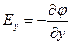 ,
, 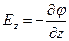 . Вектор
. Вектор  в декартовых координатах можно представить суммой
в декартовых координатах можно представить суммой
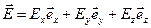 = -
= - 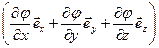 .
.
Дифференциальную операцию в скобках, примененную к скалярной функции φ, называют градиентом этой функции (grad φ). Обратите внимание: grad φ – это векторная функция, полученная дифференцированием скалярной функции φ! Таким образом, связь напряженности и потенциала выражается формулой
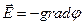 . (26)
. (26)
При решении задач бывает полезно найти проекцию  на направление некоторого вектора
на направление некоторого вектора  . Так как
. Так как 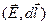 =
= 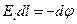 , то искомая проекция равна
, то искомая проекция равна
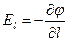 . (27)
. (27)
